Activation function
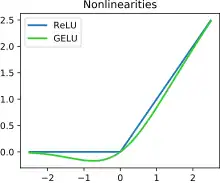
Activation function of a node in an artificial neural network is a function that calculates the output of the node (based on its inputs and the weights on individual inputs). Nontrivial problems can be solved only using a nonlinear activation function.[1] Modern activation functions include the smooth version of the ReLU, the GELU, which was used in the 2018 BERT model,[2] the logistic (sigmoid) function used in the 2012 speech recognition model developed by Hinton et al,[3] the ReLU used in the 2012 AlexNet computer vision model and in the 2015 ResNet model.
| Part of a series on |
| Machine learning and data mining |
|---|
 |
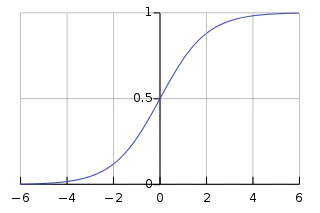
Comparison of activation functions
Aside from their empirical performance, activation functions also have different mathematical properties:
- Nonlinear
- When the activation function is non-linear, then a two-layer neural network can be proven to be a universal function approximator.[4] This is known as the Universal Approximation Theorem. The identity activation function does not satisfy this property. When multiple layers use the identity activation function, the entire network is equivalent to a single-layer model.
- Range
- When the range of the activation function is finite, gradient-based training methods tend to be more stable, because pattern presentations significantly affect only limited weights. When the range is infinite, training is generally more efficient because pattern presentations significantly affect most of the weights. In the latter case, smaller learning rates are typically necessary.
- Continuously differentiable
- This property is desirable (ReLU is not continuously differentiable and has some issues with gradient-based optimization, but it is still possible) for enabling gradient-based optimization methods. The binary step activation function is not differentiable at 0, and it differentiates to 0 for all other values, so gradient-based methods can make no progress with it.[5]
These properties do not decisively influence performance, nor are they the only mathematical properties that may be useful. For instance, the strictly positive range of the softplus makes it suitable for predicting variances in variational autoencoders.
Mathematical details
The most common activation functions can be divided into three categories: ridge functions, radial functions and fold functions.
An activation function is saturating if . It is nonsaturating if it is not saturating. Non-saturating activation functions, such as ReLU, may be better than saturating activation functions, as networks using are less likely to suffer from the vanishing gradient problem.[6]
Ridge activation functions
Ridge functions are multivariate functions acting on a linear combination of the input variables. Often used examples include:
In biologically inspired neural networks, the activation function is usually an abstraction representing the rate of action potential firing in the cell.[7] In its simplest form, this function is binary—that is, either the neuron is firing or not. Neurons also cannot fire faster than a certain rate, motivating sigmoid activation functions whose range is a finite interval.
The function looks like , where is the Heaviside step function.
If a line has a positive slope, on the other hand, it may reflect the increase in firing rate that occurs as input current increases. Such a function would be of the form .
Radial activation functions
A special class of activation functions known as radial basis functions (RBFs) are used in RBF networks, which are extremely efficient as universal function approximators. These activation functions can take many forms, but they are usually found as one of the following functions:
- Gaussian:
- Multiquadratics:
- Inverse multiquadratics:
- Polyharmonic splines
where is the vector representing the function center and and are parameters affecting the spread of the radius.
Folding activation functions
Folding activation functions are extensively used in the pooling layers in convolutional neural networks, and in output layers of multiclass classification networks. These activations perform aggregation over the inputs, such as taking the mean, minimum or maximum. In multiclass classification the softmax activation is often used.
Table of activation functions
The following table compares the properties of several activation functions that are functions of one fold x from the previous layer or layers:
| Name | Plot | Function, | Derivative of , | Range | Order of continuity |
|---|---|---|---|---|---|
| Identity | 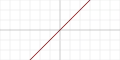 |
||||
| Binary step |  |
||||
| Logistic, sigmoid, or soft step |  |
||||
| Hyperbolic tangent (tanh) | 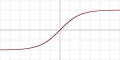 |
||||
| Soboleva modified hyperbolic tangent (smht) | 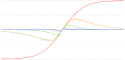 |
||||
| Rectified linear unit (ReLU)[8] |  |
||||
| Gaussian Error Linear Unit (GELU)[2] | 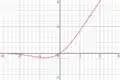 |
||||
| Softplus[9] | 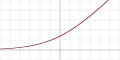 |
||||
| Exponential linear unit (ELU)[10] |  |
|
|||
| Scaled exponential linear unit (SELU)[11] | 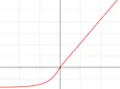 |
|
|||
| Leaky rectified linear unit (Leaky ReLU)[12] |  |
||||
| Parametric rectified linear unit (PReLU)[13] |  |
|
|||
| Sigmoid linear unit (SiLU,[2] Sigmoid shrinkage,[14] SiL,[15] or Swish-1[16]) | 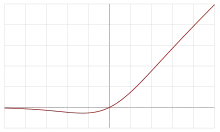 |
||||
| Gaussian |  |
The following table lists activation functions that are not functions of a single fold x from the previous layer or layers:
| Name | Equation, | Derivatives, | Range | Order of continuity |
|---|---|---|---|---|
| Softmax | for i = 1, …, J | |||
| Maxout[17] |
- ^ Here, is the Kronecker delta.
- ^ For instance, could be iterating through the number of kernels of the previous neural network layer while iterates through the number of kernels of the current layer.
Quantum activation functions
In quantum neural networks programmed on gate-model quantum computers, based on quantum perceptrons instead of variational quantum circuits, the non-linearity of the activation function can be implemented with no need of measuring the output of each perceptron at each layer. The quantum properties loaded within the circuit such as superposition can be preserved by creating the Taylor series of the argument computed by the perceptron itself, with suitable quantum circuits computing the powers up to a wanted approximation degree. Because of the flexibility of such quantum circuits, they can be designed in order to approximate any arbitrary classical activation function.[18]
References
- Hinkelmann, Knut. "Neural Networks, p. 7" (PDF). University of Applied Sciences Northwestern Switzerland. Archived from the original (PDF) on 2018-10-06. Retrieved 2018-10-06.
- Hendrycks, Dan; Gimpel, Kevin (2016). "Gaussian Error Linear Units (GELUs)". arXiv:1606.08415 [cs.LG].
- Hinton, Geoffrey; Deng, Li; Deng, Li; Yu, Dong; Dahl, George; Mohamed, Abdel-rahman; Jaitly, Navdeep; Senior, Andrew; Vanhoucke, Vincent; Nguyen, Patrick; Sainath, Tara; Kingsbury, Brian (2012). "Deep Neural Networks for Acoustic Modeling in Speech Recognition". IEEE Signal Processing Magazine. 29 (6): 82–97. doi:10.1109/MSP.2012.2205597. S2CID 206485943.
- Cybenko, G. (December 1989). "Approximation by superpositions of a sigmoidal function" (PDF). Mathematics of Control, Signals, and Systems. 2 (4): 303–314. doi:10.1007/BF02551274. ISSN 0932-4194. S2CID 3958369.
- Snyman, Jan (3 March 2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Science & Business Media. ISBN 978-0-387-24348-1.
- Krizhevsky, Alex; Sutskever, Ilya; Hinton, Geoffrey E. (2017-05-24). "ImageNet classification with deep convolutional neural networks". Communications of the ACM. 60 (6): 84–90. doi:10.1145/3065386. ISSN 0001-0782. S2CID 195908774.
- Hodgkin, A. L.; Huxley, A. F. (1952-08-28). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–544. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
- Nair, Vinod; Hinton, Geoffrey E. (2010), "Rectified Linear Units Improve Restricted Boltzmann Machines", 27th International Conference on International Conference on Machine Learning, ICML'10, USA: Omnipress, pp. 807–814, ISBN 9781605589077
- Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). "Deep sparse rectifier neural networks" (PDF). International Conference on Artificial Intelligence and Statistics.
- Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (2015-11-23). "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)". arXiv:1511.07289 [cs.LG].
- Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (2017-06-08). "Self-Normalizing Neural Networks". Advances in Neural Information Processing Systems. 30 (2017). arXiv:1706.02515.
- Maas, Andrew L.; Hannun, Awni Y.; Ng, Andrew Y. (June 2013). "Rectifier nonlinearities improve neural network acoustic models". Proc. ICML. 30 (1). S2CID 16489696.
- He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015-02-06). "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification". arXiv:1502.01852 [cs.CV].
- Atto, Abdourrahmane M.; Pastor, Dominique; Mercier, Grégoire (2008), "Smooth sigmoid wavelet shrinkage for non-parametric estimation" (PDF), 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, doi:10.1109/ICASSP.2008.4518347, S2CID 9959057
- Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2018). "Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning". Neural Networks. 107: 3–11. arXiv:1702.03118. doi:10.1016/j.neunet.2017.12.012. PMID 29395652. S2CID 6940861.
- Ramachandran, Prajit; Zoph, Barret; Le, Quoc V (2017). "Searching for Activation Functions". arXiv:1710.05941 [cs.NE].
- Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yoshua (2013). "Maxout Networks". JMLR Workshop and Conference Proceedings. 28 (3): 1319–1327. arXiv:1302.4389.
- Maronese, Marco; Destri, Claudio; Prati, Enrico (2022). "Quantum activation functions for quantum neural networks". Quantum Information Processing. 21 (4): 128. arXiv:2201.03700. doi:10.1007/s11128-022-03466-0. ISSN 1570-0755.