How to find the angles of external rays that land on the p/q root point on the boundary of Mandelbrot set's main cardioid ?

First check of p/q is irreducible

wakes
Wakes near the period 1 continent
Wakes_along_the_main_antenna
wakes up to period 10

rotation, winding numbers and regular star polygons

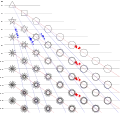
irreducible fraction

/* 
gcc i.c -Wall
./a.out
*/
#include <stdio.h>

/*
https://stackoverflow.com/questions/19738919/gcd-function-for-c
The GCD function uses Euclid's Algorithm. 
It computes A mod B, then swaps A and B with an XOR swap.
*/
int gcd(int a, int b)
{
    int temp;
    while (b != 0)
    {
        temp = a % b;

        a = b;
        b = temp;
    }
    return a;
}

int main (){

	// internal angle = n/m  in turns
	int n;  // numerator
	int d;  // denominator

 	int dMax = 17;  
 
 	for (d = 2; d <= dMax; ++d )
   		for (n = 1; n < d; ++n )
     			if (gcd(n,d)==1 ){ 
     				     			
         			printf("n/d = %d/%d\n", n,d);	// irreducible fraction  
       			} 
   
	return 0;       
}

Output:

n/d = 1/2
n/d = 1/3
n/d = 2/3
n/d = 1/4
n/d = 3/4
n/d = 1/5
n/d = 2/5
n/d = 3/5
n/d = 4/5
n/d = 1/6
n/d = 5/6
n/d = 1/7
n/d = 2/7
n/d = 3/7
n/d = 4/7
n/d = 5/7
n/d = 6/7
n/d = 1/8
n/d = 3/8
n/d = 5/8
n/d = 7/8
n/d = 1/9
n/d = 2/9
n/d = 4/9
n/d = 5/9
n/d = 7/9
n/d = 8/9
n/d = 1/10
n/d = 3/10
n/d = 7/10
n/d = 9/10
n/d = 1/11
n/d = 2/11
n/d = 3/11
n/d = 4/11
n/d = 5/11
n/d = 6/11
n/d = 7/11
n/d = 8/11
n/d = 9/11
n/d = 10/11
n/d = 1/12
n/d = 5/12
n/d = 7/12
n/d = 11/12
n/d = 1/13
n/d = 2/13
n/d = 3/13
n/d = 4/13
n/d = 5/13
n/d = 6/13
n/d = 7/13
n/d = 8/13
n/d = 9/13
n/d = 10/13
n/d = 11/13
n/d = 12/13
n/d = 1/14
n/d = 3/14
n/d = 5/14
n/d = 9/14
n/d = 11/14
n/d = 13/14
n/d = 1/15
n/d = 2/15
n/d = 4/15
n/d = 7/15
n/d = 8/15
n/d = 11/15
n/d = 13/15
n/d = 14/15
n/d = 1/16
n/d = 3/16
n/d = 5/16
n/d = 7/16
n/d = 9/16
n/d = 11/16
n/d = 13/16
n/d = 15/16
n/d = 1/17
n/d = 2/17
n/d = 3/17
n/d = 4/17
n/d = 5/17
n/d = 6/17
n/d = 7/17
n/d = 8/17
n/d = 9/17
n/d = 10/17
n/d = 11/17
n/d = 12/17
n/d = 13/17
n/d = 14/17
n/d = 15/17
n/d = 16/17

notes

external angles of p/q-wake:

have period q under doubling map. It is the same as period of landing point ( = root point )
length of periodic part of binary expansion is q
preperiod under doubling map is zero

Roots are landing points of parameter rays with periodic angles, while Misiurewicz points have preperiodic external angles.

Combinatorial algorithm = Devaney's method

Devaney's method^[1] for finding external angles of primary buds^[2]^[3]

Steps :

start with rational rotation angle,
orbit of rotation angle under circle map
translation of orbit into itinerary
conversion of itinerary into binary expansion with repeating binary fraction
conversion of binary expansion to binary fraction
conversion to decimal fraction

Input : rational rotation angle

Outpout : external angle ( decimal or binary fraction )

The code

C++

Here is C++ code from the program Mandel by Wolf Jung :

// mndcombi.cpp  by Wolf Jung (C) 2007-2015, part of Mandel 5.13, 
qulonglong mndAngle::wake(int k, int r, qulonglong &n)
{  if (k <= 0 || k >= r || r > 64) return 0LL;
   qulonglong d = 1LL; 
   int j, s = 0; 
   n = 1LL;

   for (j = 1; j < r; j++)
   {  s -= k; if (s < 0) s += r; if (!s) return 0LL;
      if (s > r - k) n += d << j;
   }
   //
   d <<= (r - 1); d--; d <<= 1; d++; //2^r - 1 for r <= 64
   return d;
}

C GMP and MPFR

/*

------- Git -----------------
cd existing_folder
git init
git remote add origin git@gitlab.com:adammajewski/wake_gmp.git
git add .
git commit -m ""
git push -u origin master
-------------------------------

?? http://stackoverflow.com/questions/2380415/how-to-cut-a-mpz-t-into-two-parts-using-gmp-lib-on-c

   
   to compile from console:
   gcc w.c -lgmp -lmpfr -Wall

    to run from console :

   ./a.out

   tested on Ubuntu 14.04 LTS

uiIADenominator = 89 
Using MPFR-3.1.2-p3 with GMP-5.1.3 with precision = 200 bits 
internal angle = 34/89
first external angle : 
period = denominator of internal angle = 89
external angle as a decimal fraction = 179622968672387565806504265/618970019642690137449562111 = 179622968672387565806504265 /( 2^89 - 1) 
External Angle as a floating point decimal number =  2.9019655713870868535821260055542440298749779423213948304299730531995503353103626302473331181359966368582651105245850405837027542373052381532777325121338632071561064451614697645709384232759475708007812e-1
external angle as a binary rational (string) : 1001010010010100101001001010010010100101001001010010100100101001001010010100100101001001/11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10010100100101001010010010100100101001010010010100101001001010010010100101001001010010010100101001001010010100100101001001010010100100101001010010010100100101001010010010100100101001010010010100101001*2^-1
external angle as a binary floating number in periodic form =0.(01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001)

                                                             .(01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001)

*/

#include <stdlib.h> // malloc
#include <stdio.h>
#include <gmp.h>  // for rational numbers 
#include <mpfr.h> // for floating point mumbers

 // rotation map 
//the number  n  is always increased by n0 modulo d

// input :  op = n/d ( rational number ) and n0 ( integer)
//  n = (n + n0 ) % d
// d = d
// output = rop = n/d
void mpq_rotation(mpq_t rop, const mpq_t op, const mpz_t n0)
{
  
  mpz_t n; // numerator
  mpz_t d; // denominator
  mpz_inits( n, d, NULL);

 
  //  
  mpq_get_num (n, op); // 
  mpq_get_den (d, op);
  
 
  // n = (n + n0 ) % d
  mpz_add(n, n, n0); 
  mpz_mod( n, n, d);
  
      
  // output
  mpq_set_num(rop, n);
  mpq_set_den(rop, d);
    
  mpz_clears( n, d, NULL);

}

void mpq_wake(mpq_t rop, mpq_t op)
{
   
  // arbitrary precision variables from GMP library
   mpz_t  n0 ; // numerator of q
   mpz_t  nc;
   mpz_t  n;
   mpz_t  d ; // denominator of q
   mpz_t  m; // 2^i

   mpz_t  num ; // numerator of rop
   mpz_t  den ; // denominator of rop
   long long int i;
   unsigned long int base = 2;
   unsigned long int id;
   int cmp;

   mpz_inits(n, n0,nc,d,num,den,m, NULL);

   mpq_get_num(n0,op);
   mpq_get_den(d,op);
   id = mpz_get_ui(d);
   //  if (n <= 0 || n >= d ) error !!!! bad input
   mpz_sub(nc, d, n0); // nc = d - n0
   mpz_set(n, n0);   
   mpz_set_ui(num, 0);

   // rop  
    // num = numerator(rop)
    
   
   // denominator = den(rop) = (2^i) -1 
   mpz_ui_pow_ui(den, base, id) ;  // den = base^id
   mpz_sub_ui(den, den, 1);   // den = den-1
   
  // numerator   
     for (i=0; i<id ; i++){  
       
       mpz_set_ui(m, 0);
       cmp = mpz_cmp(n,nc);// Compare op1 and op2. Return a positive value if op1 > op2, zero if op1 = op2, or a negative value if op1 < op2.
       if ( cmp>0 ) {
          mpz_ui_pow_ui(m, 2, id-i-1); // m = 2^(id-i   )
          mpz_add(num, num, m); // num = num + m
          if (mpz_cmp(num, den) >0) mpz_mod( num, num, den); // num = num % d ; if num==d gives 0
          //gmp_printf("s = 1");

           }
        // else gmp_printf("s = 0");
       //gmp_printf (" i = %ld internal angle = %Zd / %Zd ea = %Zd / %Zd ; m = %Zd \n", i, n, d, num, den, m);

        // n = (n + n0 ) % d = rotation 
       mpz_add(n, n, n0); 
       if (mpz_cmp(n, d)>0) mpz_mod( n, n, d);
       //
       
          
        // 
      }

    
   // rop = external angle 
   mpq_set_num(rop,num);
   mpq_set_den(rop,den);
   mpq_canonicalize (rop); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.

    
   // clear memory
   mpz_clears(n, n0, nc, d, num,den, m, NULL);

}

/*

http://stackoverflow.com/questions/9895216/remove-character-from-string-in-c

"The idea is to keep a separate read and write pointers (pr for reading and pw for writing), 
always advance the reading pointer, and advance the writing pointer only when it's not pointing to a given character."

modified

 remove first length2rmv chars and after that take only length2stay chars from input string
 output = input string 
*/
void extract_str(char* str, unsigned int length2rmv, unsigned long int length2stay) {
    // separate read and write pointers 
    char *pr = str; // read pointer
    char *pw = str; // write pointer
    int i =0; // index

    while (*pr) {
        if (i>length2rmv-1 && i <length2rmv+length2stay)
          pw += 1; // advance the writing pointer only when 
        pr += 1;  // always advance the reading pointer
        *pw = *pr;    
        i +=1;
    }
    *pw = '\0';
}

int main ()
{	

	

         // notation : 
        //number type : s = string ; q = rational ; z = integer, f = floating point
        // base : b = binary ; d = decimal

        
        char *sqdInternalAngle = "13/34";
        mpq_t qdInternalAngle;   // internal angle = rational number q = n/d
        mpz_t den;  
        unsigned long int uiIADenominator;
        
       
        mpq_t  qdExternalAngle;   // rational number q = n/d
        char  *sqbExternalAngle;
        mpfr_t  fdExternalAngle ;  // 
        char  *sfbExternalAngle; // 
        
        mp_exp_t exponent ; // holds the exponent for the result string
        mpz_t zdEANumerator;
        mpz_t zdEADenominator;
        mpfr_t EANumerator;
        mpfr_t EADenominator;
        mpfr_prec_t p = 200; // in bits , should be > denominator of internal angle

         mpfr_set_default_prec (p); // but previously initialized variables are unaffected.
        //mpfr_set_default_prec (precision);

        // init variables 
        //mpf_init(fdExternalAngle);
        mpz_inits(den, zdEANumerator,zdEADenominator, NULL);
        mpq_inits (qdExternalAngle, qdInternalAngle, NULL); //
        mpfr_inits(fdExternalAngle, EANumerator, EADenominator, NULL);

        // set variables
        mpq_set_str(qdInternalAngle, sqdInternalAngle, 10); // string is an internal angle
        mpq_canonicalize (qdInternalAngle); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.
        mpq_get_den(den,qdInternalAngle); 
        uiIADenominator = mpz_get_ui(den);
        printf("uiIADenominator = %lu \n", uiIADenominator);

        if ( p < uiIADenominator) printf("increase precision !!!!\n");         
        mpfr_printf("Using MPFR-%s with GMP-%s with precision = %u bits \n", mpfr_version, gmp_version, (unsigned int) p);

        //        
        mpq_wake(qdExternalAngle, qdInternalAngle); // internal -> external

        mpq_get_num(zdEANumerator  ,qdExternalAngle);
        mpq_get_den(zdEADenominator,qdExternalAngle); 
        // conversions
        mpfr_set_z (EANumerator,   zdEANumerator,   GMP_RNDN);
        mpfr_set_z (EADenominator, zdEADenominator, GMP_RNDN);

        sqbExternalAngle = mpq_get_str (NULL, 2, qdExternalAngle); // rational number = fraction : from decimal to binary
        
        mpfr_div (fdExternalAngle, EANumerator, EADenominator, GMP_RNDN);

        sfbExternalAngle = (char*)malloc((sizeof(char) * uiIADenominator*2*4) + 3);
        // mpfr_get_str (char *str, mpfr_exp_t *expptr, int b, size_t n, mpfr_t op, mpfr_rnd_t rnd)
        if (sfbExternalAngle==NULL ) {printf("sfbExternalAngle error \n"); return 1;}
        mpfr_get_str(sfbExternalAngle, &exponent, 2,200, fdExternalAngle, GMP_RNDN);

        // print
        gmp_printf ("internal angle = %Qd\n", qdInternalAngle); // 
        printf("first external angle : \n");
        gmp_printf ("period = denominator of internal angle = %Zd\n", den); //

        gmp_printf ("external angle as a decimal fraction = %Qd = %Zd /( 2^%Zd - 1) \n", qdExternalAngle, zdEANumerator, den); // 
        printf ("External Angle as a floating point decimal number =  ");
        mpfr_out_str (stdout, 10, p, fdExternalAngle, MPFR_RNDD); putchar ('\n');
        gmp_printf ("external angle as a binary rational (string) : %s \n", sqbExternalAngle); // 
        
        printf ("external angle as a binary floating number in exponential form =0.%s*%d^%ld\n", sfbExternalAngle, 2, exponent); 
        extract_str(sfbExternalAngle,  uiIADenominator+exponent, uiIADenominator); 
        printf ("external angle as a binary floating number in periodic form =0.(%s)\n", sfbExternalAngle);

        // clear memory
        //mpf_clear(fdExternalAngle);
        mpq_clears(qdExternalAngle, qdInternalAngle, NULL);
        mpz_clears(den, zdEANumerator, zdEADenominator, NULL);
        mpfr_clears(fdExternalAngle, EANumerator, EADenominator, NULL);
        free(sfbExternalAngle);

        return 0;
}

Examples

1/2

One can check with program Mandel :

 The 1/2-wake of the main cardioid is bounded by the parameter rays with the angles 1/3  or  p01  and 2/3  or  p10 .

1/3

Orbit of rational angle 3/7 ( and position in subintervals):

 1 / 3  = 0 
 2 / 3  = 0 
 0 / 3  = 1

so intinerary = 001

first external angle  = 001 = 1 / 7

One can check it with program Mandel by Wolf Jung : the 1/3-wake of the main cardioid is bounded by the parameter rays with the angles

1/7 or p001
2/7 or p010

note that

1/7 = 0.(001) = 0.(142857)= 0.1428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428...

1/4

The 1/4-wake of the main cardioid is
bounded by the parameter rays with the angles
1/15  or  p0001  and
2/15  or  p0010 .

n/5

There are 4 period 5 wakes:

1/5
2/5
3/5
4/5

Check it with Mandel by Wolf Jung :

The 1/5-wake of the main cardioid is bounded by the parameter rays with the angles :

1/31 or p00001
2/31 or p00010

The 4/5-wake of the main cardioid is bounded by the parameter rays with the angles

29/31 or p11101
30/31 or p11110

n/17

Angled internal address

One can check it with Mandel by Wolf Jung:

The 1/17-wake of the main cardioid is bounded by the parameter rays with the angles
* 1/131071  or  p00000000000000001 
* 2/131071  or  p00000000000000010

Web interface by Claude

.(00000000000000001)
.(00000000000000010)

1/25

uiIADenominator = 25 
Using MPFR-3.1.5 with GMP-6.1.1 with precision = 200 bits 
internal angle = 1/25
first external angle : 
period = denominator of internal angle = 25
external angle as a decimal fraction = 1/33554431 = 1 /( 2^25 - 1) 
External Angle as a floating point decimal number =  2.9802323275873758669905622896719661257256902970579355078320375103410059138021557873907862143745145987726127630324761942815747600646073471636075786857847163330961076713939572483194617724677755177253857e-8
external angle as a binary rational (string) : 1/1111111111111111111111111 
external angle as a binary floating number in exponential form =0.10000000000000000000000001000000000000000000000000100000000000000000000000010000000000000000000000001000000000000000000000000100000000000000000000000010000000000000000000000001000000000000000000000001*2^-24
external angle as a binary floating number in periodic form =0.(0000000000000000000000001)

So 1/25-wake of the main cardioid is bounded by the parameter rays with the angles :

0.0000000298 = 1/33554431 = 1 /( 2^25 - 1) = 0.(0000000000000000000000001)
0,0000000596 = 2/33554431 = 2 /( 2^25 - 1) = 0.(0000000000000000000000010)

One can check it with Mandel

The angle  1/33554431  or  p0000000000000000000000001
has  preperiod = 0  and  period = 25.
The conjugate angle is  2/33554431  or  p0000000000000000000000010 .
The kneading sequence is  AAAAAAAAAAAAAAAAAAAAAAAA*  and
the internal address is  1-25 .
The corresponding parameter rays are landing at the root of a satellite component of period 25.
It is bifurcating from period 1.
Do you want to draw the rays and to shift c
to the corresponding center?

The center is :

 c = 0.265278321904606  +0.003712059989878 i    period = 25

3/7

Parabolic Julia set for internal angle 3 over 7 with 2 external rays and labelled components

Rotation with rational angle 3 over 7

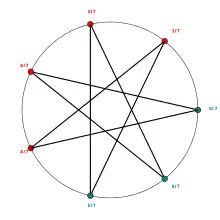
wake 3/7

Divide interval ( circle):

 $I={\big (}0,1{\big ]}$

into 2 subintervals ( lower partition) :

 $I_{0}={\big (}{\tfrac {0}{7}},{\tfrac {4}{7}}{\big ]}$

 $I_{1}={\big (}{\tfrac {4}{7}},{\tfrac {7}{7}}{\big ]}$

Orbit of rational angle 3/7 ( and position in subintervals):

So itinerary is :

  $0101001$

One can convert it to number :

$0101001\to 0.(0101001)_{2}={\frac {0101001}{1111111}}_{2}={\frac {41}{127}}_{10}$

One can check it with program Mandel by Wolf Jung :

The 3/7-wake of the main cardioid is
bounded by the parameter rays with the angles
41/127  or  p0101001  and
42/127  or  p0101010 .

root point :

 c = -0.606356884415893  +0.412399740175787 i

Orbit of 41/127 under doubling map modulo 1 computed with this program ( exponent = 7 and mpz_init_set_ui(n, 41); :

1/31

Mandelbrot set - wake 1 over 31 with external rays

The 1/31-wake of the main cardioid

is bounded by the parameter rays with the angles 1/2147483647 or p0000000000000000000000000000001 and 2/2147483647 or p0000000000000000000000000000010
root point : c = 0.260025517721190 +0.002060296266000 i
center c = 0.260025517721190 +0.002060296266000 i
principal Misiurewicz point c = 0.259995759918769 +0.001610271381965*i
- has preperiod = 31 , period = 1
- is a landing point for 31 external rays
  - 2147483649/4611686016279904256 = 0000000000000000000000000000001p0000000000000000000000000000010 = .0000000000000000000000000000001(0000000000000000000000000000010)
the biggest baby Mandelbrot set has the kneading sequence AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB* corresponds to the internal address 1-31-32 . The period is 32. The smallest angles are 3/4294967295 = 0.(00000000000000000000000000000011) and 4/4294967295 = 0.(00000000000000000000000000000100)

On the dynamical plane :

The angle

13/34

Rotation with rational angle 13/34

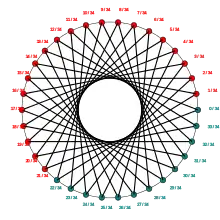
Output from program Mandel by Wolf Jung :

The 13/34-wake of the main cardioid is
bounded by the parameter rays with the angles
4985538889/17179869183  or  p0100101001001010010100100101001001  and
4985538890/17179869183  or  p0100101001001010010100100101001010 .

 s = 0 i = 0 internal angle = 13 / 34 ea = 0 / 17179869183 ; m = 0 
s = 1 i = 1 internal angle = 26 / 34 ea = 4294967296 / 17179869183 ; m = 4294967296 
s = 0 i = 2 internal angle = 5 / 34 ea = 4294967296 / 17179869183 ; m = 0 
s = 0 i = 3 internal angle = 18 / 34 ea = 4294967296 / 17179869183 ; m = 0 
s = 1 i = 4 internal angle = 31 / 34 ea = 4831838208 / 17179869183 ; m = 536870912 
s = 0 i = 5 internal angle = 10 / 34 ea = 4831838208 / 17179869183 ; m = 0 
s = 1 i = 6 internal angle = 23 / 34 ea = 4966055936 / 17179869183 ; m = 134217728 
s = 0 i = 7 internal angle = 2 / 34 ea = 4966055936 / 17179869183 ; m = 0 
s = 0 i = 8 internal angle = 15 / 34 ea = 4966055936 / 17179869183 ; m = 0 
s = 1 i = 9 internal angle = 28 / 34 ea = 4982833152 / 17179869183 ; m = 16777216 
s = 0 i = 10 internal angle = 7 / 34 ea = 4982833152 / 17179869183 ; m = 0 
s = 0 i = 11 internal angle = 20 / 34 ea = 4982833152 / 17179869183 ; m = 0 
s = 1 i = 12 internal angle = 33 / 34 ea = 4984930304 / 17179869183 ; m = 2097152 
s = 0 i = 13 internal angle = 12 / 34 ea = 4984930304 / 17179869183 ; m = 0 
s = 1 i = 14 internal angle = 25 / 34 ea = 4985454592 / 17179869183 ; m = 524288 
s = 0 i = 15 internal angle = 4 / 34 ea = 4985454592 / 17179869183 ; m = 0 
s = 0 i = 16 internal angle = 17 / 34 ea = 4985454592 / 17179869183 ; m = 0 
s = 1 i = 17 internal angle = 30 / 34 ea = 4985520128 / 17179869183 ; m = 65536 
s = 0 i = 18 internal angle = 9 / 34 ea = 4985520128 / 17179869183 ; m = 0 
s = 1 i = 19 internal angle = 22 / 34 ea = 4985536512 / 17179869183 ; m = 16384 
s = 0 i = 20 internal angle = 1 / 34 ea = 4985536512 / 17179869183 ; m = 0 
s = 0 i = 21 internal angle = 14 / 34 ea = 4985536512 / 17179869183 ; m = 0 
s = 1 i = 22 internal angle = 27 / 34 ea = 4985538560 / 17179869183 ; m = 2048 
s = 0 i = 23 internal angle = 6 / 34 ea = 4985538560 / 17179869183 ; m = 0 
s = 0 i = 24 internal angle = 19 / 34 ea = 4985538560 / 17179869183 ; m = 0 
s = 1 i = 25 internal angle = 32 / 34 ea = 4985538816 / 17179869183 ; m = 256 
s = 0 i = 26 internal angle = 11 / 34 ea = 4985538816 / 17179869183 ; m = 0 
s = 1 i = 27 internal angle = 24 / 34 ea = 4985538880 / 17179869183 ; m = 64 
s = 0 i = 28 internal angle = 3 / 34 ea = 4985538880 / 17179869183 ; m = 0 
s = 0 i = 29 internal angle = 16 / 34 ea = 4985538880 / 17179869183 ; m = 0 
s = 1 i = 30 internal angle = 29 / 34 ea = 4985538888 / 17179869183 ; m = 8 
s = 0 i = 31 internal angle = 8 / 34 ea = 4985538888 / 17179869183 ; m = 0 
s = 0 i = 32 internal angle = 21 / 34 ea = 4985538888 / 17179869183 ; m = 0 
s = 1 i = 33 internal angle = 34 / 34 ea = 4985538889 / 17179869183 ; m = 1 
internal angle = 13/34
period = denominator of internal angle = 34
external angle as a decimal fraction = 4985538889/17179869183 = 4985538889 /( 2^34 - 1) 
external angle as a binary rational (string) : 100101001001010010100100101001001/1111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.1001010010010100101001001010010010100101001001010010100100101001*2^-1
external angle as a binary floating number in periodic form =0.(0100101001001010010100100101001)

34/89

Using GMP-5.1.3 with precision = 256 bits 
internal angle = 34/89
period = denominator of internal angle = 89
external angle as a decimal fraction = 179622968672387565806504265/618970019642690137449562111
external angle as a binary rational (string) : 1001010010010100101001001010010010100101001001010010100100101001001010010100100101001001/11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10010100100101001010010010100100101001010010010100101001001010010010100101001001010010010100101001001010010100100101001001010010100100101001010010010100100101001010010010100100101001010010010100101001001010010010100101001001010010100100101001001010010100101*2^-1
external angle as a binary floating number in periodic form =0.(01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001)

1/128

uiIADenominator = 128 
Using MPFR-4.0.2 with GMP-6.2.0 with precision = 200 bits 
internal angle = 1/128
first external angle : 
period = denominator of internal angle = 128
external angle as a decimal fraction = 1/340282366920938463463374607431768211455 = 1 /( 2^128 - 1) 
External Angle as a floating point decimal number =  2.9387358770557187699218413430556141945553000604853132483972656175588435482079339324933425313850237034701685918031624270579715075034722882265605472939461496635969950989468319466936530037770580747746862e-39
external angle as a binary rational (string) : 1/11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000000*2^-127
external angle as a binary floating number in periodic form =0.(00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001)

89/268

External rays landing on the 89/268 wake

Using GMP-5.1.3 with precision = 320 bits 
internal angle = 89/268
period = denominator of internal angle = 268
external angle as a decimal fraction = 67754913930863876636420964942226524366713408170066250043659752013773168429311121/474284397516047136454946754595585670566993857190463750305618264096412179005177855
external angle as a binary rational (string) : 0010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010001
/1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010001
001001001001001001001001001001001001001001001001001001*2^-2
external angle as a binary floating number in periodic form =
0.(0010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010001)

References

Bifurcation in Complex Quadrat ic Polynomial and Some Folk Theorems Involving the Geometry of Bulbs of the Mandelbrot Set by Monzu Ara Begum

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] The Mandelbrot Set and The Farey Tree by Robert L. Devaney

[2] External angles in the Mandelbrot set: the work of Douady and Hubbard by Douglas C. Ravenel

[3] Complex number and the Mandelbrot set by Dusa McDuff and Melkana Brakalova

[1]

[2]

[3]