The doubling map

How to find the period of angle under doubling map

visual
numerical
- read period from denominator of decimal fraction ( reduced rational fraction m/n )
- find period/preperiod in the binary expansion ( binary sequence)
  - string matching algorithms, for instance, naive or brute-force search, Knuth-Morris-Pratt algorithm^[1]
  - discrete Fourier transform
- read it from the itinerary of angle under doubling map

Period of binary expansion of reduced rational fraction m/n is equal to the multiplicative order of 2 modulo n:

$Period_{2}(m/n)={ord}_{n}(2)$

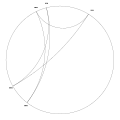orbit of angle 5/31 under doubling map
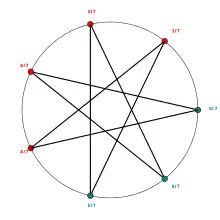rotation with rational angle 3 over 7

C version

double precision: forward and inverse doubling map

/*


doubling map 
en.wikipedia.org/wiki/Dyadic_transformation

2*t mod 1 



how to invert doubling map  



Inverse of doubling map is multivalued function: 2 preimages
t/2 and  (t+1)/2
to choose proper preimage one needs extra information from forward iteration = itinerary





itinerary : list of symbols 
for  coding the orbits of a given dynamical system 
by partitioning the space X and forming an itinerary 



http://www.maths.qmul.ac.uk/~sb/cf_chapter4.pdf


see also how to convert proper decimal fraction to binary fraction

commons.wikimedia.org/wiki/File:Binary_decomposition_of_dynamic_plane_for_f0(z)_%3D_z%5E2.png



---------- git -------------------- 
cd existing_folder
git init
git remote add origin git@gitlab.com:adammajewski/doubling_map.git
git add .
git commit -m "Initial commit"
git push -u origin master



*/
#include <stdio.h> // printf
#include <math.h> // fabs


#define iMax  8 //

int main(){

	double t0 ;
	double t ;
	double ti; // final t after iMax iterations
	double tr; //
	double dt;
	
	int itinerary[iMax]= {0};
	
	
	
	
	
	int i;
	
	
	t0 = (double) 1/7;
	t = t0;
	
	// check the input : it should be   0.0 <= t < 1.0
	if (t>1.0) {printf("t is > 1.0\n"); return 1;}
	if (t<0.0) {printf("t is < 0.0\n"); return 1;}
	
	
	printf("forward iteration of doubling map\n");
	for(i=0; i<iMax; i++){
	        
	        printf("t%d = %f", i, t);
	        // https://en.wikipedia.org/wiki/Dyadic_transformation
		t = t*2.0; // doubling 
		if (t>1.0) {	
			
			itinerary[i]= 1;
			t = t - 1.0; 
			printf(" wrap\n");} // modulo 1 
			else printf("\n");
		}
	printf("t%d = %f\n", i, t);	
		
	//		
	ti = t;	
	
	printf("\nbackward iteration of doubling map = halving map \n");
	
	//
	for(i=iMax; i>0; i--){ // reverse counting
	        
	        printf("t%d = %f", i, t);
	        
	        if (itinerary[i-1]==1) { // i-1 !!! 
	        	 
	        	t = t + 1.0; 
	        	printf(" unwrap\n");} // modulo 1 
			else printf("\n");
	        t = t/2.0; // halving 
		
		}
	printf("t%d = %f\n", i, t);	
		
			
         tr = t;		
		
		
	//
	printf("\n\nresults \n");
	printf("t0 = %f\n", t0);	
	printf("t%d = %f\n", iMax, ti);
	
	dt = fabs(t0- tr);
	printf("tr = %f\n", tr);
	printf("dt = fabs(t0- tr) = %f\n", dt );
	printf("\nitinerary:\n");
	for(i=0; i<iMax; i++) printf("itinerary[%d] = %d \n", i, itinerary[i]);
	
	
	printf("\ndecimal %f has binary expansion = 0.", t0);
	for(i=0; i<iMax; i++) printf("%d", itinerary[i]);
	printf("\n");
	
	if (dt < 0.0000000001) printf("program works good !\n");
		else printf("program fails !\n");
	
		

	return 0;}

arbitrary precision

// gcc d.c -lgmp -Wall

#include <stdio.h>
#include <gmp.h>

//  a multiple precision integer, as defined by the GMP library. The C data type for such integers is mpz_t

int print_z(mpz_t  z, int base, char *s){
  printf("%s= ", s);
  mpz_out_str (stdout, 10, z);
  printf (" for base = %d\n", base);
  return 0;
}

// rop = (2*op) mod 1
// wikipedia : dyadic_transformation or doubling map
void mpq_doubling(mpq_t rop, const mpq_t op)
{
  mpz_t n; // numerator
  mpz_t d; // denominator
  mpz_inits(n, d, NULL);

 
  //  
  mpq_get_num (n, op); // 
  mpq_get_den (d, op); 
 
  // n = (n * 2 ) % d
  mpz_mul_ui(n, n, 2); 
  mpz_mod( n, n, d);
  
      
  // output
  mpq_set_num(rop, n);
  mpq_set_den(rop, d);
    
  mpz_clears(n, d, NULL);

}

int main ()
{

        int i;
        //
        unsigned long int e = 89; // exponent is also a period of doubling map 
        unsigned long int b = 2;
       
        // arbitrary precision variables from GMP library
        mpz_t  n ; // numerator of q
        mpz_t  d ; // denominator of q
        mpq_t q;   // rational number q = n/d

        // init and set variables 
        mpz_init_set_ui(n, 1);

        // d = (2^e) -1 
        // http://fraktal.republika.pl/mset_external_ray.html
        mpz_init(d);
        mpz_ui_pow_ui(d, b, e) ;  // d = b^e
        mpz_sub_ui(d, d, 1);   // d = d-1

        //   q = n/d
        mpq_init (q); //
        mpq_set_num(q,n);
        mpq_set_den(q,d);
        mpq_canonicalize (q); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.

        // print 
        //print_z(d, 10, "d ");
        //print_z(n, 10, "n ");
        gmp_printf ("q = %Qd\n",q); //  
        
        // 
        for (i=0; i<(1+2*e) ; i++){  
          mpq_doubling(q, q);
          gmp_printf ("q = %Qd\n",q); // 
        }   
         
       
        
        
        // clear memory
        mpq_clear (q);
        mpz_clears(n, d, NULL);
        
        
        return 0;
}

C++ version

/*
based on : 
   mndcombi.cpp  by Wolf Jung (C) 2010. 
   http://mndynamics.com/indexp.html 
   which is the part of Mandel 5.5 
   multiplatform C++ GUI program using QT 
   on the same licence as above

 "The function is computing the preperiod and period (of n/d under doubling map)
 and setting the denominator to  2^preperiod*(2^period - 1) if possible.
 So 1/5 becomes 3/15 and 2/10 becomes 3/15 as well.
 The period is returned as the value of the function, 
 n and d are changed ( Arguments passed to function by reference)
 and the preperiod is returned in k." (Wolf Jung)
 Question : if result is >=0 why do not use unsigneg char or unsigned int for type of result ???

*/
int normalize(unsigned long long int &n, unsigned long long int &d, int &k)
{  if (!d) return 0; // d==0 error
   n %= d; 
   while (!(n & 1) && !(d & 1)) { n >>= 1; d >>= 1; }
   int p; 
   unsigned long long int n0, n1 = n, d1 = d, np;
   k = 0; 
   while (!(d1 & 1)) { k++; d1 >>= 1; if (n1 >= d1) n1 -= d1; }
   n0 = n1;
   for (p = 1; p <= 65 - k; p++) 
	{ twice(n1, d1); 
	  if (n1 == n0) break; }
   if (k + p > 64) return 0; // more then max unsigned long long int
   np = 1LL; 
   np <<= (p - 1); 
   np--; np <<= 1; 
   np++; //2^p - 1 for p <= 64
   n0 = np; 
   d >>= k; n1 = d; 
   if (n1 > n0) { n1 = n0; n0 = d; }
   while (1) { d1 = n0 % n1; if (!d1) break; 
   n0 = n1; n1 = d1; } //gcd n1
   n /= d/n1; 
   n *= np/n1; 
   d = np << k;
   return p;
}

Lisp version

(defun give-period (ratio-angle)
	"gives period of angle in turns (ratio) under doubling map"
	(let* ((n (numerator ratio-angle))
	       (d (denominator ratio-angle))
	       (temp n)) ; temporary numerator
	  
	  (loop for p from 1 to 100 do 
		(setq temp  (mod (* temp 2) d)) ; (2 x n) modulo d = doubling)
		when ( or (= temp n) (= temp 0)) return p )))

Maxima CAS version

DoublingMap(r):=
block([d,n],
 n:ratnumer(r),
 d:ratdenom(r),
 mod(2*n,d)/d)$

/*
Tests : 
GivePeriod (1/7)
3
GivePeriod (1/14) 
0
GivePeriod (1/32767)
15
GivePeriod (65533/65535)
16

Gives 0 if :
* not periodic ( preperiodic )
* period >pMax
*/

GivePeriod (r):=
block([rNew, rOld, period, pMax, p],
      pMax:100,
      period:0,
       
      p:1, 
      rNew:DoublingMap(r),
      while ((p<pMax) and notequal(rNew,r)) do
        (rOld:rNew,
         rNew:DoublingMap(rOld),
         p:p+1
        ),
      if equal(rNew,r) then period:p,
      period
);

Haskell version

Haskell version^[2]

Conversion from an integer type (Int or Integer) to anything else is done by "fromIntegral". The target type is inferred automatically

-- by Claude Heiland-Allen
-- import Data.List (findIndex, groupBy)
-- type N = Integer
-- type Q = Rational
 period :: Q -> N
 period p =
  let Just i = (p ==) `findIndex` drop 1 (iterate double p)
  in  fromIntegral i + 1

Real quadratic map

Complex quadratic map

"Critically preperiodic polynomials are typically parameterized by the angle θ of the external ray landing at the critical value rather than by the critical value." MARY WILKERSON^[3]

checking the period using position of parameter = periodicity checking

Finding period of the orbit

/* mndynamo.cpp  by Wolf Jung (C) 2007-2015.  Defines classes:
   mndynamics, mndsiegel, mndcubesiegel, mndquartsiegel, mndexposiegel,
   mndtrigosiegel, mndexpo, mndtrigo, mndmatesiegel, mndmating, mndsingpert,
   mndherman, mndnewtonsiegel, mndnewton, mndcubicnewton, mndquarticnewton

   These classes are part of Mandel 5.13, which is free software; you can
   redistribute and / or modify them under the terms of the GNU General
   Public License as published by the Free Software Foundation; either
   version 3, or (at your option) any later version. In short: there is
   no warranty of any kind; you must redistribute the source code as well.
*/
uint mndynamics::period(double &a, double &b, int cycle) // = 0
{  //determine the period, if cycle then set a, b to periodic point.
   uint j; double x, y, x0, y0; critical(a, b, x, y);
   for (j = 1; j <= 1000; j++)
   { if (x*x + y*y <= bailout) f(a, b, x, y); else return 0; }
   x0 = x; y0 = y;
   for (j = 1; j <= 1024; j++)
   {  if (x*x + y*y <= bailout) f(a, b, x, y); else return 0;
      if ( (x - x0)*(x - x0) + (y - y0)*(y - y0) < 1e-16)
      {  if (cycle) { a = x; b = y; }
         return j;
      }
   }
   return 10000;
}

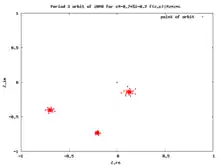critical orbit with 3-period cycle
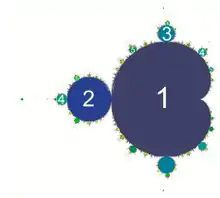periodic components of M set
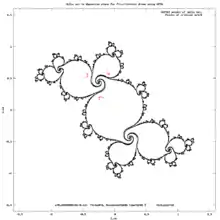Drawing Julia set and critical orbit. Computing period
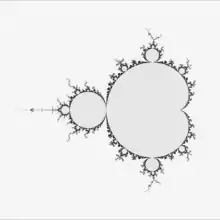Computing period for drawing Mandelbrot set

Methods :

direct period detection from iterations
the spider algorithm
"methods based on interval arithmetic when implemented properly are capable of finding all period-n cycles for considerable large n." (ZBIGNIEW GALIAS )^[4]
Floyd's cycle-finding algorithm ^[5]

Finding period is used to :

Period of critical orbit

Finding period of critical orbit using forward iteration of critical point :

Maxima CAS

/*
 b batch file for maxima
*/

kill(all);
remvalue(all);

/* =================== functions ============ */

/*
 https://en.wikibooks.org/wiki/Fractals/Iterations_in_the_complex_plane/qpolynomials
complex quadratic polynomial
*/

f(z,c):=z*z+c;

/* iterated map */

fn(p, z, c) :=
  if p=0 then z
  elseif p=1 then f(z,c)
  else f(fn(p-1, z, c),c);

/* 
https://en.wikibooks.org/wiki/Fractals/Mathematics/Period#Complex_quadratic_map

period of c under complex quadratic polynomial f
*/
GivePeriod(c):=block(

[z: 0.0,
 k2Max:200, /* to big values couse bind stack overflow */
 k1Max:100,
 ER:2.0,
 dMax:0.0003, /* if too low then gives smaller period then */
 period:0 /* no period found = (period > k2Max) or ..... ????  */

],

/* to remove non periodic points , iterate and do not use it */
for k1:1 thru k1Max  do 
  (z: f(z,c),
   if  (cabs(z)>ER) then  (period : -1, /* escaping */ 
                           go(exit))
  ),

/* after k1Max iterations z SHOULD BE inside periodic orbit   */   
zOld:z,

for k2:1 thru k2Max  do  
 ( z: f(z,c), 
   if  (cabs(z)>ER) then  (period : -1,  go(exit)), /* escaping */
   if  (cabs(zOld-z)<dMax) then  (period : k2,  go(exit)) /* periodic */
  ),

exit,

return(period)

)$

/*

Tests :

good
G(0)
G(-1.75)
G(-1.77)
G(-1.778)
G(-0.155+0.75*%i)    period = 3
G(-1.7577+0.0138*%i)     period = 9
G(-0.615341000000000  +0.423900000000000*%i);    period = 7
G(-1.121550281113895  +0.265176187855967*%i);    period = 18)

Tuning : 
0 period ( when true period > k2Max
G(-1.119816337988403  +0.264371090395906*%i); 
gives 0 when k2Max =100
gives 108 when dMax = 0.003
but  true period = 162  ( set k2Max = 200 and dMax= 0.0003

-------------------
G(0.37496784+%i*0.21687214);
http://fraktal.republika.pl/period.html
gives 0

*/

G(c):=GivePeriod(c);

compile(all);
/* -------- input value ------ */

c : 0.25  +0.5 * %i$

/* ============== compute ===============  */
p:GivePeriod(c)$
p;

c

code by Claude

Comparison of 2 functions for finding a period :

/*
gcc p.c -Wall -lm 
time ./a.out
numerical approximation of period of limit cycle 
Adam Majewski
*/

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

long double ER2 = 4.0L;
unsigned int jMax = 1000; // iteration max = Max period

// mndynamics::period(double &a, double &b, int cycle)
// mndynamo.cpp  by Wolf Jung (C) 2007-2014
// part of Mandel 5.10 which is free software; you can
//   redistribute and / or modify them under the terms of the GNU General
//   Public License as published by the Free Software Foundation; either
//   version 3, or (at your option) any later version. In short: there is
//   no warranty of any kind; you must redistribute the source code as well.
/*

void mndlbrot::f(double a, double b, double &x, double &y) const
{ double u = x*x - y*y + a; y = 2*x*y + b; x = u; }
*/
unsigned int GivePeriodJung(long double cx, long double cy, long double ER2, unsigned int jMax, long double precision2, long double Zp[2]) 
{  //determine the period, then set Zp to periodic point.
   // bailout = ER2 = (EscapeRadius)^2
   unsigned int j;
  // unsigned int jMax = 500000; 
   long double x=0.0L;
   long double y=0.0L; // z 
   long double x0, y0; // z0 inside periodic orbit
   long double t; // temp
   //long double precision = 1e-16;
   
   // iterate until z fall into periodic cycle ( = limit cycle) 
   for (j = 1; j <= jMax; j++)
   { 
     if (x*x + y*y <= ER2) 
       {t = x*x - y*y + cx; 
        y = 2*x*y + cy; 
        x = t;}
       else return 0; //escaping = definitely not periodic 
   } 
   // after jMax iterations z SHOULD BE inside periodic orbit 
   x0 = x; y0 = y; // z = z0

   // find a period 
   for (j = 1; j <= jMax; j++)
   {  
      if (x*x + y*y <= ER2) 
        {t = x*x - y*y + cx; 
        y = 2*x*y + cy; 
        x = t;}
        else return 0; // escaping = definitely not periodic
      
     if ( (x - x0)*(x - x0) + (y - y0)*(y - y0) < precision2) // periodic 
      {   Zp[0] = x; 
          Zp[1] = y; 
         return j;  // period = j 
      }
   }
   return (2*jMax+3); // (not escaping after 2*jMax = maybe periodic but period > jMax) or  
    // (maybe escaping but slow dynamics, so need more iterations then 2*jMax) 
}

int SameComplexValue(long double Z1x,long double Z1y,long double Z2x,long double Z2y, long double precision)
{
    if (fabsl(Z1x-Z2x)<precision && fabs(Z1y-Z2y)<precision) 
       return 1; /* true */
       else return 0; /* false */
    }
 
/*-------------------------------*/
// this function is based on program:
// Program MANCHAOS.BAS  
// http://sprott.physics.wisc.edu/chaos/manchaos.bas
// (c) 1997 by J. C. Sprott 
//
unsigned int GivePeriodS(long double Cx,long double Cy, unsigned int iMax, long double precision, long double Zp[2])
{  
 
 
  long double Zx2, Zy2, /* Zx2=Zx*Zx;  Zy2=Zy*Zy  */
         ZPrevieousX,ZPrevieousY,
         ZNextX,ZNextY;
 
     unsigned int i; 
     unsigned int  period = iMax+3; // not periodic or period > iMax

     /* dynamic 1D arrays for  x, y of z points   */
    long double *OrbitX; // zx
    long double *OrbitY;  // zy 
     int iLength = iMax; // length of arrays ;  array elements are numbered from 0 to iMax-1 
  //  creates dynamic arrays and checks if it was done properly
  OrbitX = malloc( iLength * sizeof(long double) );
  OrbitY = malloc( iLength * sizeof(long double) );
  if (OrbitX == NULL || OrbitY ==NULL)
    {
      printf("Could not allocate memory \n");
      return 1; // error
    }

 
  Zp[0] = 0.0;
  Zp[1] = 0.0;

  /* starting point is critical point  */
   ZPrevieousX=0.0;
   ZPrevieousY=0.0;
   OrbitX[0] =0.0;
   OrbitY[0] =0.0;  
   Zx2=ZPrevieousX*ZPrevieousX;
   Zy2=ZPrevieousY*ZPrevieousY;

   /* iterate and save points to the array */
   for (i=0;i<iMax ;i++)
        {
            ZNextY=2*ZPrevieousX*ZPrevieousY + Cy;
            ZNextX=Zx2-Zy2 +Cx;
            Zx2=ZNextX*ZNextX;
            Zy2=ZNextY*ZNextY;
            if ((Zx2+Zy2)>ER2) return 0; /* basin of atraction to infinity */
            //if (SameComplexValue(ZPrevieousX,ZPrevieousY,ZNextX,ZNextY,precision))
            //   return 1; /* fixed point , period =1 */
            ZPrevieousX=ZNextX;
            ZPrevieousY=ZNextY;
            /* */
            OrbitX[i] = ZNextX;
            OrbitY[i] = ZNextY;   
 
        };
 
    /* find   */    
     for(i=iMax-2;i>0;i--) 
      if (SameComplexValue(OrbitX[iMax-1],OrbitY[iMax-1],OrbitX[i],OrbitY[i],precision))
        { 
          Zp[0] = OrbitX[i];
          Zp[1] = OrbitY[i]; 
          period = iMax-i-1; // compute period 
          break; // the loop 
        }
   
  // free memmory
  free(OrbitX);
  free(OrbitY);

  return period ; 
}

unsigned int GivePeriodReal(long double Cx,long double Cy)
{
 // check
  
  if ( -0.75L<Cx && Cx<0.25L ) return 1;
  if ( -1.25L<Cx && Cx<-0.75L ) return 2;
  if ( -1.368089448988708L<Cx && Cx<-1.25L ) return 4; // numerical approximation = maybe wrong
  if ( -1.394040000725660L<Cx && Cx<-1.368089448988708L ) return 8; // numerical approximation = maybe wrong
 return 0; // -1.36809742955000002314

}

int main()

{
// THE REAL SLICE OF THE MANDELBROT SET 
long double CxMin = -1.4011551890L; // The Feigenbaum Point = the limit of the period doubling cascade of bifurcations 
long double CxMax = -0.74L;  
long double Cx;
long double Cy = 0.0L;
long double PixelWidth = (CxMax-CxMin)/10000.0L;
long double precisionS = PixelWidth / 100.0L;
long double precisionJ = 1e-16; 
unsigned int periodS, periodJ, periodR;
long double Zp[2]; // periodic z points on dynamic plane
unsigned int iMax = 1000000; // iteration max = Max period 
                    
// text file 
FILE * fp;  // result is saved to text file 
fp = fopen("data2p10pz.txt","w"); // create new file,give it a name and open it in binary mode  
fprintf(fp," periods of attracting orbits ( c points ) on real axis of parameter plane = real slice of the Mandelbrot set  \n");
fprintf(fp," from Cmin = %.20Lf to Cmax = %.20Lf \n", CxMin, CxMax);
fprintf(fp," dC = CxMax-CxMin = %.20Lf \n", CxMax- CxMin);
fprintf(fp," PixelWidth       = %.20Lf \n", PixelWidth);
fprintf(fp," precisionS        = %.20Lf ; precisionJ =  %.20Lf\n", precisionS, sqrtl(precisionJ));
fprintf(fp," iMaxS = %u ; iMaxJ = %u\n", iMax, 2*jMax);
fprintf(fp," \n\n\n");

// go along real axis from CxMin to CxMax using linear scale 
Cx = CxMin;
while (Cx<CxMax)
{ 
  // compute 
  periodR = GivePeriodReal(Cx,Cy);
  periodS = GivePeriodS(Cx, Cy, iMax, precisionS, Zp);
  periodJ = GivePeriodJung(Cx, Cy, ER2, jMax, precisionJ, Zp);
  // check and save 
  if (periodR>0)
    {
      if (periodJ==periodS && periodS==periodR ) // all periods are the same and real period is known 
         fprintf(fp," c = %.20Lf ; period = %u ; \n", Cx, periodS );
         else fprintf(fp," c = %.20Lf ; period = %u ; periodS = %u ; periodJ = %u ; difference !!! \n", Cx, periodR, periodS, periodJ );
    }
    else // PeriodR==00
     {
       if (periodJ==0 && periodS==0 ) 
         fprintf(fp," c = %.20Lf ; period = %u ; \n", Cx, periodS );// all periods are the same and real period is known 
         else { if (periodS==periodJ)
                fprintf(fp," c = %.20Lf ; periodJ = periodS = %u ; \n", Cx, periodS );
                else fprintf(fp," c = %.20Lf ; periodS = %u ; periodJ = %u ; difference !!! \n", Cx, periodS, periodJ );
              }
      }  
  // info message
  printf("c = %.20Lf \n",Cx);
  // next c point 
  Cx += PixelWidth;
}

 fclose(fp);
 printf(" result is saved to text file \n");
return 0;
}

Non-linear scale shows bigger periods ( along real slice of Mandelbrot set ) :

/*

gcc p.c -Wall -lm 
time ./a.out

numerical approximation  of limit cycle's period  
along real slice of Mandelbrot set

Adam Majewski

*/

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

// part of THE REAL SLICE OF THE MANDELBROT SET where period doubling cascade is  
long double CxMin = -1.4011552; // 1890L; // > The Feigenbaum Point = the limit of the period doubling cascade of bifurcations 
long double CxMax = 0.26L;  
long double Cx;
long double Cy = 0.0L; // constant value 
long double PixelWidth ; // = (CxMax-CxMin)/10000.0L;
//long double precisionS ; //precisionS = PixelWidth / 100.0L;//= PixelWidth / 100.0L;
long double f= 4.669201609102990671853203820466L; // The Feigenbaum delta constant 
long double precisionJ = 1e-20; 
unsigned int periodJ, periodR;
long double Zp[2]; // periodic z points on dynamic plane

long double ER2 = 4.0L;
unsigned int jMax = 5000000; // iteration max = Max period 
unsigned int iNoPeriod;
//unsigned int iMax ; //= 2*jMax; // 1000000; // iteration max = Max period

// mndynamics::period(double &a, double &b, int cycle)
// mndynamo.cpp  by Wolf Jung (C) 2007-2014
// part of Mandel 5.10 which is free software; you can
//   redistribute and / or modify them under the terms of the GNU General
//   Public License as published by the Free Software Foundation; either
//   version 3, or (at your option) any later version. In short: there is
//   no warranty of any kind; you must redistribute the source code as well.
/*

void mndlbrot::f(double a, double b, double &x, double &y) const
{ double u = x*x - y*y + a; y = 2*x*y + b; x = u; }

code with small changes

*/
unsigned int GivePeriodJung(long double cx, long double cy, long double ER2, unsigned int jMax, long double precision2, long double Zp[2]) 
{  //determine the period, then set Zp to periodic point.
   // bailout = ER2 = (EscapeRadius)^2
   unsigned int j;
  // unsigned int jMax = 500000; 
   long double x=0.0L;
   long double y=0.0L; // z 
   long double x0, y0; // z0 inside periodic orbit
   long double t; // temp
   //long double precision = 1e-16;
   
   // iterate until z fall into periodic cycle ( = limit cycle) 
   for (j = 1; j <= jMax; j++)
   { 
     if (x*x + y*y <= ER2) 
       {t = x*x - y*y + cx; 
        y = 2*x*y + cy; 
        x = t;}
       else return 0; //escaping = definitely not periodic 
   } 
   // after jMax iterations z SHOULD BE inside periodic orbit 
   x0 = x; y0 = y; // z = z0

   // find a period 
   for (j = 1; j <= jMax; j++)
   {  
      if (x*x + y*y <= ER2) 
        {t = x*x - y*y + cx; 
        y = 2*x*y + cy; 
        x = t;}
        else return 0; // escaping = definitely not periodic
      
     if ( (x - x0)*(x - x0) + (y - y0)*(y - y0) < precision2) // periodic 
      {   Zp[0] = x; 
          Zp[1] = y; 
         return j;  // period = j 
      }
   }
   return (iNoPeriod); // (not escaping after 2*jMax = maybe periodic but period > jMax) or  
    // (maybe escaping but slow dynamics, so need more iterations then 2*jMax) 
}

// http://classes.yale.edu/Fractals/MandelSet/MandelScalings/CompDiam/CompDiam.html
unsigned int GivePeriodReal(long double Cx,long double Cy)
{
 long double Cx0= 0.25L; 
 long double Cx1= -0.75L; 
 long double Cx2= -1.25L; 
 long double Cx3= -1.368089448988708L; // numerical approximation = maybe wrong
 long double Cx4= -1.394040000725660L; // numerical approximation = maybe wrong
  
  if ( Cx1<Cx && Cx<Cx0 ) return 1;
  if ( Cx2<Cx && Cx<Cx1 ) return 2;
  if ( Cx3<Cx && Cx<Cx2 ) return 4; // numerical approximation = maybe wrong
  if ( Cx4<Cx && Cx<Cx3 ) return 8; // numerical approximation = maybe wrong
 return 0; // -1.36809742955000002314

}

// try to have the same number of the pixels = n
// inside each hyperbolic component of Mandelbrot set along real axis
// width of components

long double GivePixelWidth(unsigned int period, unsigned int n)
{

  long double w ;
  unsigned int k;

 switch ( period )
 {  // A SCALING CONSTANT EQUAL TO UNITY IN 1D QUADRATIC MAPS M. ROMERA, G. PASTOR and F. MONTOYA
   case      0 : w=(CxMax-CxMin)/n;      break;
   case      1 : w=1.000000000000L/n;    break; // exact value
   case      2 : w=0.310700264133L/n;    break; // numerical approximation , maybe wrong 
   case      4 : w=0.070844843095L/n;    break; // w(2*p) = w(p)/f  ; f =  Feigenbaum constant
   case      8 : w=0.015397875272L/n;    break;
   case     16 : w=0.003307721510L/n;    break;
   case     32 : w=0.000708881730L/n;    break;
   case     64 : w=0.000151841994935L/n; break;
   case    128 : w=0.000032520887170L/n; break;
   case    256 : w=0.00000696502297L/n;  break;
   case    512 : w=0.000001491696694L/n; break;
   case   1024 : w=0.000000319475846L/n; break;
   case   2048 : w=0.000000068421948L/n; break;
   case   4096 : w=0.000000015L/n;       break;
   case   8192 : w=0.000000004L/n;       break;
   case  16384 : w=0.000000001L/n;       break;
   default : if (period == 2*jMax+3)  w=(CxMax-CxMin)/10.0L; // period not found or period > jMax
                else { k=period/16384; w = 0.000000001L; while (k>2) { w /=f; k /=2;};  w /=n;} // feigenbaum scaling  
 }

 return w;
}

int main()

{

PixelWidth = (CxMax-CxMin)/1000.0L;
precisionJ = PixelWidth/10000000.0L;
iNoPeriod = 2*jMax+3;
                    
// text file 
FILE * fp;  // result is saved to text file 
fp = fopen("data64_50ff.txt","w"); // create new file,give it a name and open it in binary mode  
fprintf(fp," periods of attracting orbits ( c points ) on real axis of parameter plane = real slice of the Mandelbrot set  \n");
fprintf(fp," from  Cmax = %.20Lf to Cmin = %.20Lf \n", CxMax, CxMin);
fprintf(fp," dC = CxMax-CxMin = %.20Lf \n", CxMax- CxMin);
fprintf(fp," non-inear scale with varied step = PixelWidth       \n");
fprintf(fp," precisionJ =  %.20Lf\n", sqrtl(precisionJ));
fprintf(fp,"  jMax = %u\n",  2*jMax);
fprintf(fp," \n\n\n");

// go along real axis from CxMin to CxMax using linear scale 
Cx = CxMax;
while (Cx>CxMin)
{ 
  // compute 
  //periodR = GivePeriodReal(Cx,Cy);
  periodJ = GivePeriodJung(Cx, Cy, ER2, jMax, PixelWidth/10000000.0L, Zp);
  // check and save 
   if (periodJ == iNoPeriod) 
      fprintf(fp," c = %.20Lf ; periodJ = %u ; PixelWidth = %.20LF Period not found : error !!! \n", Cx, periodJ, PixelWidth );
      else fprintf(fp," c = %.20Lf ; periodJ = %u ; PixelWidth = %.20LF \n", Cx, periodJ, PixelWidth );
  printf("c = %.20Lf ; period = %u \n",Cx, periodJ);  // info message
  // next c point 
  PixelWidth =GivePixelWidth( periodJ, 50);
  Cx -= PixelWidth;
}

 fclose(fp);
 printf(" result is saved to text file \n");

return 0;
}