The Böttcher function of which maps the complement of the Mandelbrot set ( Julia set) conformally to the complement of the closed unit disk.

Complex potential on the parameter plane

Gradient of the potential

Complex potential

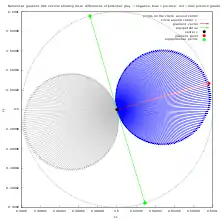
Complex potential on dynamical plane

Exterior or complement of filled-in Julia set is :

a basin of attraction of infinity ( superattracting fixed point) so dynamics in ttah basin is the same for all polynomials !!!
one of components of the Fatou set

$A_{f_{c}}(\infty )=K(f_{c})^{C}=F_{\infty }$

It can be analysed using

escape time (simple but gives only radial values = escape time ) LSM/J,
distance estimation ( more advanced, continuus, but gives only radial values = distance ) DEM/J
Boettcher coordinate or complex potential ( the best )

" The dynamics of polynomials is much better understood than the dynamics of general rational maps" due to the Bottcher’s theorem^[1]

Superattracting fixed points

For complex quadratic polynomial there are many superattracting fixed point ( with multiplier = 0 ):

infinity ( It is always is superattracting fixed point for polynomials )
$z_{s}=0\,$ is finite superattracting fixed point for map $f_{0}\,$
$z_{s}=0\,$ and $z_{s}=-1\,$ are two finite superattracting fixed points for map $f_{-1}\,$

Description

Near^[2] super attracting fixed point (for example infinity) the behaviour of discrete dynamical system :

$z_{n+1}=f_{c}(z_{n})=z_{n}^{2}+c\,$

based on complex quadratic polynomial $f_{c}(z)=z^{2}+c\,$ is similar to

$w_{n+1}=f_{0}(w_{n})=w_{n}^{2}\,$

based on $f_{0}(w)=w^{2}\,$

It can be treated as one dynamical system viewed in two coordinate systems :

easy ( w )
hard to analyse( z )

^[3]

In other words map $f_{c}\,$ is conjugate ^[4] to map $f_{0}\,$ near infinity.^[5]

Names

$w\,$ is Boettcher coordinate
$\Phi _{c}\,$ is Boettcher function^[6]
Boettcher Functional Equation:^[7]^[8]

  $\Phi _{c}(f_{c}(z))=\Phi _{c}(z)^{2}\,$

where :

  $w=\Phi _{c}(z)\,$

Complex potential or Boettcher coordinate has :

radial values ( real potential ) LogPhi = CPM/J = value of the Green's function
angular values ( external angle ) ArgPhi

Both values can be used to color with 2D gradient.

Computation

Formula from Mathemathica^[9]

$w=B(c,z)=\lim _{n\to \infty }z_{n}^{\frac {1}{2^{n}}}\,$

To compute Boettcher coordinate $w\,$ use this formula ^[10]

$w=\Phi _{c}(z)=z*\prod _{n=1}^{\infty }\left({\frac {f_{c}^{n}(z)}{f_{c}^{n}(z)-c}}\right)^{1/2^{n}}\,$

It looks "simple", but :

square root of complex number gives two values so one have to choose one value
more precision is needed near Julia set

explicit closed form solution

c = 0
c = -2

c = -2

polar coordinate system and Psi_c for c=-2

For c = -2 Julia set is a horizontal segment between -2 and 2 on the real axis:^[11]

 $\ K_{-2}\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C$

Now:

equipotential lines are elipses
field lines are hyperbolas
Boettcher map and it's inverse have explicit equations ( closed-form expression^[12] ):

 $\Phi _{-2}(z)={\frac {z+{\sqrt {z^{2}-4}}}{2}}\,$

 $\Phi ^{-1}(w)=w+{\frac {1}{w}}\,$

where branch cut is taken to coincide with $\ K_{-2}$

History

In 1904 LE Boettcher:^[14]

solved Schröder functional equation^[15]^[16] in case of supperattracting fixed point^[17]^[18]
"proved the existence of an analytic function $\phi (z)\sim z$ near $\infty$ which conjugates the polynomial with $z^{d}$ , that is $\phi \circ p(z)=\phi (z)^{d}$ " ( Alexandre Eremenko ) ^[19]

LogPhi - Douady-Hubbard potential - real potential - radial component of complex potential

The potential function and the real iteration number

The Julia set for $f(z)=z^{2}$ is the unit circle, and on the outer Fatou domain, the potential function φ(z) is defined by φ(z) = log|z|. The equipotential lines for this function are concentric circles. As $|f(z)|=|z|^{2}$ we have

\varphi (z)=\lim _{k\to \infty }{\frac {\log |z_{k}|}{2^{k}}},

where $z_{k}$ is the sequence of iteration generated by z. For the more general iteration $f(z)=z^{2}+c$ , it has been proved that if the Julia set is connected (that is, if c belongs to the (usual) Mandelbrot set), then there exist a biholomorphic map ψ between the outer Fatou domain and the outer of the unit circle such that $|\psi (f(z))|=|\psi (z)|^{2}$ .^[20] This means that the potential function on the outer Fatou domain defined by this correspondence is given by:

\varphi (z)=\lim _{k\to \infty }{\frac {\log |z_{k}|}{2^{k}}}.

This formula has meaning also if the Julia set is not connected, so that we for all c can define the potential function on the Fatou domain containing ∞ by this formula. For a general rational function f(z) such that ∞ is a critical point and a fixed point, that is, such that the degree m of the numerator is at least two larger than the degree n of the denominator, we define the potential function on the Fatou domain containing ∞ by:

\varphi (z)=\lim _{k\to \infty }{\frac {\log |z_{k}|}{d^{k}}},

where d = m − n is the degree of the rational function.^[21]

If N is a very large number (e.g. 10¹⁰⁰), and if k is the first iteration number such that $|z_{k}|>N$ , we have that

{\frac {\log |z_{k}|}{d^{k}}}={\frac {\log(N)}{d^{\nu (z)}}},

for some real number $\nu (z)$ , which should be regarded as the real iteration number, and we have that:

\nu (z)=k-{\frac {\log(\log |z_{k}|/\log(N))}{\log(d)}},

where the last number is in the interval [0, 1).

For iteration towards a finite attracting cycle of order r, we have that if z* is a point of the cycle, then $f(f(...f(z^{*})))=z^{*}$ (the r-fold composition), and the number

\alpha ={\frac {1}{\left|(d(f(f(\cdots f(z))))/dz)_{z=z^{*}}\right|}}\qquad (>1)

is the attraction of the cycle. If w is a point very near z* and w' is w iterated r times, we have that

\alpha =\lim _{k\to \infty }{\frac {|w-z^{*}|}{|w'-z^{*}|}}.

Therefore the number $|z_{kr}-z^{*}|\alpha ^{k}$ is almost independent of k. We define the potential function on the Fatou domain by:

\varphi (z)=\lim _{k\to \infty }{\frac {1}{(|z_{kr}-z^{*}|\alpha ^{k})}}.

If ε is a very small number and k is the first iteration number such that $|z_{k}-z^{*}|<\epsilon$ , we have that

\varphi (z)={\frac {1}{(\varepsilon \alpha ^{\nu (z)})}}

for some real number $\nu (z)$ , which should be regarded as the real iteration number, and we have that:

\nu (z)=k-{\frac {\log(\varepsilon /|z_{k}-z^{*}|)}{\log(\alpha )}}.

If the attraction is ∞, meaning that the cycle is super-attracting, meaning again that one of the points of the cycle is a critical point, we must replace α by

\alpha =\lim _{k\to \infty }{\frac {\log |w'-z^{*}|}{\log |w-z^{*}|}},

where w' is w iterated r times and the formula for φ(z) by:

\varphi (z)=\lim _{k\to \infty }{\frac {\log(1/|z_{kr}-z^{*}|)}{\alpha ^{k}}}.

And now the real iteration number is given by:

\nu (z)=k-{\frac {\log(\log |z_{k}-z^{*}|/\log(\varepsilon ))}{\log(\alpha )}}.

For the colouring we must have a cyclic scale of colours (constructed mathematically, for instance) and containing H colours numbered from 0 to H−1 (H = 500, for instance). We multiply the real number $\nu (z)$ by a fixed real number determining the density of the colours in the picture, and take the integral part of this number modulo H.

The definition of the potential function and our way of colouring presuppose that the cycle is attracting, that is, not neutral. If the cycle is neutral, we cannot colour the Fatou domain in a natural way. As the terminus of the iteration is a revolving movement, we can, for instance, colour by the minimum distance from the cycle left fixed by the iteration.

CPM/J

Potential of filled Julia set

Diagram of potential computed with 2 methods : simple and full

Note that potential inside Kc is zero so :

Pseudocode version :

if (LastIteration==IterationMax)
 then potential=0    /* inside  Filled-in Julia set */
 else potential= GiveLogPhi(z0,c,ER,nMax); /* outside */

It also removes potential error for log(0).

Full version

Math (full) notation :^[22]

$LogPhi_{c}(z)=ln|z|+\sum _{n=1}^{\infty }{\frac {1}{2^{n}}}ln|1+{\frac {c}{(f_{c}^{n-1}(z))^{2}}}|$

Maxima (full) function :

GiveLogPhi(z0,c,ER,nMax):=
block(
 [z:z0,
 logphi:log(cabs(z)),
 fac:1/2,
 n:0],
 while n<nMax and abs(z)<ER do
 (z:z*z+c,
 logphi:logphi+fac*log(cabs(1+c/(z*z))),
 n:n+1
 ),
 return(float(logphi))
)$

Simplified version

The escape rate function of a polynomial f is defined by :

$G_{f}(z)=\lim _{n\rightarrow \infty }{\frac {1}{2^{n}}}log^{+}|f^{n}(z)|\,$

where :

$log^{+}=max(log,0)$

"The function Gp is continous on C and harmonic on the complement of the Julia set. It vanishes identically on K(f) and as it has a logarithmic pole at infinity, it is a it is the Green's function for C/ K(f)." ( Laura G. DeMarco) ^[23]

Math simplified formula :

$SLogPhi_{c}(z)={\frac {log(f^{n}(z))}{2^{n}}}\,$

Maxima function :

GiveSLogPhi(z0,c,e_r,i_max):=
 block(
  [z:z0,
   logphi,
   fac:1/2,
   i:0
  ],
  while i<i_max and cabs(z)<e_r do
  (z:z*z+c,
    fac:fac/2,
    i:i+1
  ),
 logphi:fac*log(cabs(z)),
 return(float(logphi))
)$

If you don't check if orbit is not bounded ( escapes, bailout test) then use this Maxima function :

GiveSLogPhi(z0,c,e_r,i_max):=
block(
 [z:z0, logphi, fac:1/2, i:0],
  while i<i_max and cabs(z)<e_r do
   (z:z*z+c,
    fac:fac/2,
    i:i+1 ),
   if i=i_max
    then logphi:0
    else logphi:fac*log(cabs(z)),
   float(logphi) 
)$

C version :

double jlogphi(double zx0, double zy0, double cx, double cy)
/* this function is based on function by W Jung http://mndynamics.com */
{ 
 int j; 
 double 
 zx=zx0,
 zy=zy0,
 s = 0.5, 
 zx2=zx*zx,
 zy2=zy*zy,
 t;
 for (j = 1; j < 400; j++)
 { s *= 0.5; 
  zy = 2 * zx * zy + cy;
  zx = zx2 - zy2 + cx; 
  zx2 = zx*zx; 
  zy2 = zy*zy;
  t = fabs(zx2 + zy2); // abs(z)
  if ( t > 1e24) break; 
 } 
return s*log2(t);  // log(zn)* 2^(-n)
}//jlogphi

Euler version by R. Grothmann ( with small change : from z^2-c to z^2+c) :^[24]

function iter (z,c,n=100) ...

h=z;
loop 1 to n;
h=h^2+c;
if totalmax(abs(h))>1e20; m=#; break; endif;
end;
return {h,m};
endfunction

x=-2:0.05:2; y=x'; z=x+I*y;
{w,n}=iter(z,c);
wr=max(0,log(abs(w)))/2^n;

Level Sets of potential = pLSM/J

Here is Delphi function which gives level of potential :

Function GiveLevelOfPotential(potential:extended):integer;
 var r:extended;
 begin
    r:= log2(abs(potential));
    result:=ceil(r);
 end;

Level Curves of potential = equipotential lines = pLCM/J

The continuous potential formula doesn't align properly with iteration bands

ArgPhi - External angle (angular component of complex potential) and external ray

One can start with binary decomposition of basin of attraction of infinity.

The second step can be using $\Psi _{c}\,$

period detection

How to find period of external angle measured in turns under doubling map :

Here is Common Lisp code :

(defun give-period (ratio-angle)
  "gives period of angle in turns (ratio) under doubling map"
  (let* ((n (numerator ratio-angle))
	 (d (denominator ratio-angle))
	 (temp n)) ; temporary numerator
    
    (loop for p from 1 to 100 do 
	  (setq temp  (mod (* temp 2) d)) ; (2 x n) modulo d = doubling)
	  when ( or (= temp n) (= temp 0)) return p )))

Maxima CAS code :

doubling_map(n,d):=mod(2*n,d);

/* catch-throw version by Stavros Macrakis, works */
GivePeriodOfAngle(n0,d):=
catch(
      block([ni:n0],
          for i thru 200 do if (ni:doubling_map(ni,d))=n0 then throw(i),
          0 ) )$

/* go-loop version, works */
GiveP(n0,d):=block(
[ni:n0,i:0],
block(
  loop,
  ni:doubling_map(ni,d),
  i:i+1,
  if i<100 and not (n0=ni) then go(loop)
),
if (n0=ni) 
	then i 
	else 0
);

/* Barton Willis while version without for loop , works */
GivePeriod(n0,d):=block([ni : n0,k : 1],
  while (ni : doubling_map(ni,d)) # n0 and k < 100 do (
    k : k + 1),
  if k = 100 then 0 else k)$

Computing external angle

External angle (argument) is argument of Boettcher coordinate $w\,$

$arg_{c}(z)=arg(w)=arg(\Phi _{c}(z))\,$

Because Boettcher coordinate is a product of complex numbers

$w=\Phi _{c}(z)=z*\prod _{n=1}^{\infty }\left({\frac {f_{c}^{n}(z)}{f_{c}^{n}(z)-c}}\right)^{1/2^{n}}\,$

so argument of product is :

$arg_{c}(z)=arg(z)+\sum _{n=1}^{\infty }\left({\frac {1}{2^{n}}}*arg\left({\frac {f_{c}^{n}(z)}{f_{c}^{n}(z)-c}}\right)\right)\,$

Constructing the spine of filled Julia set

Algorithm for constructiong the spine is described by A. Douady^[25]

join $-\beta \,$ and $\beta \,$ ,
(to do )

Drawing dynamic external ray

Field lines in in the Fatou domain

Explanation by Gert Buschmann

The equipotential lines for iteration towards infinity

Field lines for an iteration of the form

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

In each Fatou domain (that is not neutral) there are two systems of lines orthogonal to each other: the equipotential lines (for the potential function or the real iteration number) and the field lines.

If we colour the Fatou domain according to the iteration number (and not the real iteration number $\nu (z)$ , as defined in the previous section), the bands of iteration show the course of the equipotential lines. If the iteration is towards ∞ (as is the case with the outer Fatou domain for the usual iteration $z^{2}+c$ ), we can easily show the course of the field lines, namely by altering the colour according as the last point in the sequence of iteration is above or below the x-axis (first picture), but in this case (more precisely: when the Fatou domain is super-attracting) we cannot draw the field lines coherently - at least not by the method we describe here. In this case a field line is also called an external ray.

Let z be a point in the attracting Fatou domain. If we iterate z a large number of times, the terminus of the sequence of iteration is a finite cycle C, and the Fatou domain is (by definition) the set of points whose sequence of iteration converges towards C. The field lines issue from the points of C and from the (infinite number of) points that iterate into a point of C. And they end on the Julia set in points that are non-chaotic (that is, generating a finite cycle). Let r be the order of the cycle C (its number of points) and let z* be a point in C. We have $f(f(\dots f(z^{*})))=z^{*}$ (the r-fold composition), and we define the complex number α by

\alpha =(d(f(f(\dots f(z))))/dz)_{z=z^{*}}.

If the points of C are $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ , α is the product of the r numbers $f'(z_{i})$ . The real number 1/|α| is the attraction of the cycle, and our assumption that the cycle is neither neutral nor super-attracting, means that 1 < 1/|α| < ∞. The point z* is a fixed point for $f(f(\dots f(z)))$ , and near this point the map $f(f(\dots f(z)))$ has (in connection with field lines) character of a rotation with the argument β of α (that is, $\alpha =|\alpha |e^{\beta i}$ ).

In order to colour the Fatou domain, we have chosen a small number ε and set the sequences of iteration $z_{k}(k=0,1,2,\dots ,z_{0}=z)$ to stop when $|z_{k}-z^{*}|<\epsilon$ , and we colour the point z according to the number k (or the real iteration number, if we prefer a smooth colouring). If we choose a direction from z* given by an angle θ, the field line issuing from z* in this direction consists of the points z such that the argument ψ of the number $z_{k}-z^{*}$ satisfies the condition that

\psi -k\beta =\theta \mod \pi .\,

For if we pass an iteration band in the direction of the field lines (and away from the cycle), the iteration number k is increased by 1 and the number ψ is increased by β, therefore the number $\psi -k\beta \mod \pi$ is constant along the field line.

Pictures in the field lines for an iteration of the form

z^{2}+c

A colouring of the field lines of the Fatou domain means that we colour the spaces between pairs of field lines: we choose a number of regularly situated directions issuing from z*, and in each of these directions we choose two directions around this direction. As it can happen that the two field lines of a pair do not end in the same point of the Julia set, our coloured field lines can ramify (endlessly) in their way towards the Julia set. We can colour on the basis of the distance to the center line of the field line, and we can mix this colouring with the usual colouring. Such pictures can be very decorative (second picture).

A coloured field line (the domain between two field lines) is divided up by the iteration bands, and such a part can be put into a one-to-one correspondence with the unit square: the one coordinate is (calculated from) the distance from one of the bounding field lines, the other is (calculated from) the distance from the inner of the bounding iteration bands (this number is the non-integral part of the real iteration number). Therefore, we can put pictures into the field lines (third picture).

backwards iteration

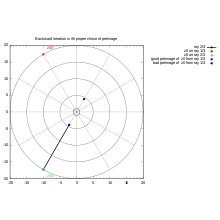
Backward iteration of complex quadratic polynomial with proper choice of the preimage

This method has been used by several people and proved by Thierry Bousch.^[26]

Code in c++ by Wolf Jung can be found in procedure QmnPlane::backray() in file qmnplane.cpp ( see source code of the program Mandel ).^[27]

Ray for periodic angle ( simplest case )

It will be explained by an example :

First choose external angle $t\,$ (in turns). External angle for periodic ray is a rational number.

t={\frac {1}{3}}\,

Compute period of external angle under doubling map.

Because "1/3 doubled gives 2/3 and 2/3 doubled gives 4/3, which is congruent to 1/3" ^[28]

1\equiv 2{\pmod {3}}.\,

or

{\frac {2}{3}}\equiv {\frac {1}{3}}{\pmod {1}}.\,

^[29]

so external angle $t={\frac {1}{3}}\,$ has period 2 under doubling map.

Start with 2 points near infinity (in conjugate plane):

on ray 1/3 is a point $w=R*e^{2\pi i/3}\,$

on ray 2/3 is a point $w=R*e^{4\pi i/3}\,$ .

Near infinity $z=w\,$ so one can swith to dynamical plane ( Boettcher conjugation )

Backward iteration (with proper chose from two possibilities)^[30] of point on ray 1/3 goes to ray 2/3, back to 1/3 and so on.

In C it is :

/* choose one of 2 roots: zNm1 or -zNm1  where zN = sqrt(zN - c )  */
if (creal(zNm1)*creal(zN) + cimag(zNm1)*cimag(zN) <= 0) zNm1=-zNm1;

or in Maxima CAS :

if (z1m1.z01>0) then z11:z1m1 else z11:-z1m1;

One has to divide set of points into 2 subsets ( 2 rays). Draw one of these 2 sets and join the points. It will be an approximation of ray.

Ray for preperiodic angle ( to do )

/*

compute last point ~ landing point
of the dynamic ray for periodic angles ( in turns )

 gcc r.c -lm -Wall -march=native

landing point of ray for angle = 1 / 15 = 0.0666666666666667 is = (0.0346251977103306 ;  0.4580500411138030 ) ; iDistnace = 18 
landing point of ray for angle = 2 / 15 = 0.1333333333333333 is = (0.0413880816505388 ;  0.5317194187688231 ) ; iDistnace = 17 
landing point of ray for angle = 4 / 15 = 0.2666666666666667 is = (-0.0310118081927549 ;  0.5440125864026020 ) ; iDistnace = 17 
landing point of ray for angle = 8 / 15 = 0.5333333333333333 is = (-0.0449867688014234 ;  0.4662592852362425 ) ; iDistnace = 18

*/

// https://gitlab.com/adammajewski/ray-backward-iteration
#include <stdio.h>
#include <stdlib.h> // malloc
#include <math.h> // M_PI; needs -lm also 
#include <complex.h>

/* --------------------------------- global variables and consts ------------------------------------------------------------ */
#define iPeriodChild 4 // iPeriodChild of secondary component joined by root point

// - --------------------- functions ------------------------

/* 
   principal square  root of complex number 
   wikipedia  Square_root

   z1= I;
   z2 = root(z1);
   printf("zx  = %f \n", creal(z2));
   printf("zy  = %f \n", cimag(z2));
*/
double complex root(double x, double y)
{ 
  
  double u;
  double v;
  double r = sqrt(x*x + y*y); 
  
  v = sqrt(0.5*(r - x));
  if (y < 0) v = -v; 
  u = sqrt(0.5*(r + x));
  return u + v*I;
}

// This function only works for periodic  angles.
// You must know the iPeriodChild n before calling this function.
// draws all "iPeriodChild" external rays 
// commons  File:Backward_Iteration.svg
// based on the code by Wolf Jung from program Mandel
// http://www.mndynamics.com/

int ComputeRays( //unsigned char A[],
			    int n, //iPeriodChild of ray's angle under doubling map
			    int iterMax,
                            double Cx, 
                            double Cy,
                            double dAlfaX,
                            double dAlfaY,
                            double PixelWidth,
                            complex double zz[iPeriodChild] // output array

			    )
{
  double xNew; // new point of the ray
  double yNew;
  
  const double R = 10000; // very big radius = near infinity
  int j; // number of ray 
  int iter; // index of backward iteration

  double t,t0; // external angle in turns 
  double num, den; // t = num / den
  
  double complex zPrev;
  double u,v; // zPrev = u+v*I
 
  int iDistance ; // dDistance/PixelWidth = distance to fixed in pixels

  
  /* dynamic 1D arrays for coordinates ( x, y) of points with the same R on preperiodic and periodic rays  */
  double *RayXs, *RayYs;
  int iLength = n+2; // length of arrays ?? why +2

  //  creates arrays :  RayXs and RayYs  and checks if it was done
  RayXs = malloc( iLength * sizeof(double) );
  RayYs = malloc( iLength * sizeof(double) );
  if (RayXs == NULL || RayYs==NULL)
    {
      fprintf(stderr,"Could not allocate memory");
      getchar(); 
      return 1; // error
    }

   // external angle of the first ray 
   num = 1.0;
   den = pow(2.0,n) -1.0;
   t0 = num/den; // http://fraktal.republika.pl/mset_external_ray_m.html
   t=t0;
   // printf(" angle t = %.0f / %.0f = %f in turns \n", num, den, t0);

  //  starting points on preperiodic and periodic rays 
  //  with angles t, 2t, 4t...  and the same radius R
  for (j = 0; j < n; j++)
    { // z= R*exp(2*Pi*t)
      RayXs[j] = R*cos((2*M_PI)*t); 
      RayYs[j] = R*sin((2*M_PI)*t);
      //
      // printf(" %d angle t = = %.0f / %.0f =  %.16f in turns \n", j, num , den,  t); 
      //
      num *= 2.0;
      t *= 2.0; // t = 2*t
      if (t > 1.0) t--; // t = t modulo 1
      
    }
  //zNext = RayXs[0] + RayYs[0] *I;

  // printf("RayXs[0]  = %f \n", RayXs[0]);
  // printf("RayYs[0]  = %f \n", RayYs[0]);

  // z[k] is n-periodic. So it can be defined here explicitly as well.
  RayXs[n] = RayXs[0]; 
  RayYs[n] = RayYs[0];

  //   backward iteration of each point z
  for (iter = -10; iter <= iterMax; iter++)
    { 
     	
      for (j = 0; j < n; j++) // n +preperiod
	{ // u+v*i = sqrt(z-c)   backward iteration in fc plane 
	  zPrev = root(RayXs[j+1] - Cx , RayYs[j+1] - Cy ); // , u, v
	  u=creal(zPrev);
	  v=cimag(zPrev);
                
	  // choose one of 2 roots: u+v*i or -u-v*i
	  if (u*RayXs[j] + v*RayYs[j] > 0) 
	    { xNew = u; yNew = v; } // u+v*i
	  else { xNew = -u; yNew = -v; } // -u-v*i

	  // draw part of the ray = line from zPrev to zNew
	 // dDrawLine(A, RayXs[j], RayYs[j], xNew, yNew, j, 255);
                
	  
	  //  
	  RayXs[j] = xNew; RayYs[j] = yNew;
                
	

                
	} // for j ...

          //RayYs[n+k] cannot be constructed as a preimage of RayYs[n+k+1]
      RayXs[n] = RayXs[0]; 
      RayYs[n] = RayYs[0];
          
      // convert to pixel coordinates 
      //  if z  is in window then draw a line from (I,K) to (u,v) = part of ray 
   
      // printf("for iter = %d cabs(z) = %f \n", iter, cabs(RayXs[0] + RayYs[0]*I));
     
    }

  // aproximate end of ray by straight line to it's landing point here = alfa fixed point
 // for (j = 0; j < n + 1; j++)
  //  dDrawLine(A, RayXs[j],RayYs[j], dAlfaX, dAlfaY,j, 255 );

  // this check can be done only from inside this function
  t=t0;
  num = 1.0;
  for (j = 0; j < n ; j++)
    {

      zz[j] = RayXs[j] +  RayYs[j] * I; // save to the output array
      // aproximate end of ray by straight line to it's landing point here = alfa fixed point
      //dDrawLine(RayXs[j],RayYs[j], creal(alfa), cimag(alfa), 0, data); 
      iDistance = (int) round(sqrt((RayXs[j]-dAlfaX)*(RayXs[j]-dAlfaX) +  (RayYs[j]-dAlfaY)*(RayYs[j]-dAlfaY))/PixelWidth);
      printf("last point of the ray for angle = %.0f / %.0f = %.16f is = (%.16f ;  %.16f ) ; Distance to fixed = %d  pixels \n",num, den, t, RayXs[j], RayYs[j],  iDistance);
      num *= 2.0;
      t *= 2.0; // t = 2*t
      if (t > 1) t--; // t = t modulo 1
    } // end of the check

  // free memmory
  free(RayXs);
  free(RayYs);

  return  0; //  
}

int main()
{
  
  complex double l[iPeriodChild];
  int i;
  // external angle in turns = num/den; 
  double num = 1.0;
  double den = pow(2.0, iPeriodChild) -1.0;

   ComputeRays( iPeriodChild, 
                   10000, 
                   0.25, 0.5, 
                   0.00, 0.5,
                   0.003,
                   l ) ;

  
  printf("\n see what is in the output array : \n");

  for (i = 0; i < iPeriodChild ; i++) {
       printf("last point of the ray for angle = %.0f / %.0f = %.16f is = (%.16f ;  %.16f ) \n",num, den, num/den, creal(l[i]), cimag(l[i]));
       num *= 2.0;}

  return 0;
}

Run it :

./a.out

And output :

last point of the ray for angle = 1 / 15 = 0.0666666666666667 is = (0.0346251977103306 ;  0.4580500411138030 ) ; Distance to fixed = 18  pixels 
last point of the ray for angle = 2 / 15 = 0.1333333333333333 is = (0.0413880816505388 ;  0.5317194187688231 ) ; Distance to fixed = 17  pixels 
last point of the ray for angle = 4 / 15 = 0.2666666666666667 is = (-0.0310118081927549 ;  0.5440125864026020 ) ; Distance to fixed = 18  pixels 
last point of the ray for angle = 8 / 15 = 0.5333333333333333 is = (-0.0449867688014234 ;  0.4662592852362425 ) ; Distance to fixed = 19  pixels

 see what is in the output array : 
last point of the ray for angle = 1 / 15 = 0.0666666666666667 is = (0.0346251977103306 ;  0.4580500411138030 ) 
last point of the ray for angle = 2 / 15 = 0.1333333333333333 is = (0.0413880816505388 ;  0.5317194187688231 ) 
last point of the ray for angle = 4 / 15 = 0.2666666666666667 is = (-0.0310118081927549 ;  0.5440125864026020 ) 
last point of the ray for angle = 8 / 15 = 0.5333333333333333 is = (-0.0449867688014234 ;  0.4662592852362425 )

Point on the ray is moving backwards:

very fast when it it far from Julia set
very slow near Julia set ( after 50 iterations distance between points = 0 pixels )

See example computing ( here pixel size = 0.003 ) :

# iteration distance_between_points_in_pixels
0 	 3300001 
1 	 30007 
2 	 2296 
3 	 487 
4 	 179 
5 	 92 
6 	 54 
7 	 34 
8 	 23 
9 	 18 
10 	 14 
11 	 11 
12 	 9 
13 	 7 
14 	 6 
15 	 5 
16 	 5 
17 	 4 
18 	 4 
19 	 3 
20 	 3 
21 	 3 
22 	 3 
23 	 2 
24 	 2 
25 	 2 
26 	 2 
27 	 2 
28 	 2 
29 	 2 
30 	 1 
31 	 1 
32 	 1 
33 	 1 
34 	 1 
35 	 1 
36 	 1 
37 	 1 
38 	 1 
39 	 1 
40 	 1 
41 	 1 
42 	 1 
43 	 1 
44 	 1 
45 	 1 
46 	 1 
47 	 1 
48 	 1 
49 	 1 
50 	 1 
51 	 1 
52 	 1 
53 	 1 
54 	 1 
55 	 1 
56 	 0 
57 	 0 
58 	 0 
59 	 0 
60 	 0

One can choose points which differ by pixel size :

#iteration    distance(z1,z2)   distance (z,alfa)
       0 	 3300001 	 33368
       1 	   30007 	  3364
       2 	    2296 	  1074
       3 	     487 	   591
       4 	     179 	   413
       5 	      92 	   321
       6 	      54 	   267
       7 	      34 	   234
       8 	      23 	   211
       9 	      18 	   193
      10 	      14 	   179
      11 	      11 	   169
      12 	       9 	   160
      13 	       7 	   153
      14 	       6 	   146
      15 	       5 	   141
      16 	       5 	   136
      17 	       4 	   132
      18 	       4 	   128
      19 	       3 	   125
      20 	       3 	   122
      21 	       3 	   119
      22 	       3 	   117
      23 	       2 	   115
      24 	       2 	   112
      25 	       2 	   110
      26 	       2 	   109
      27 	       2 	   107
      28 	       2 	   105
      29 	       2 	   104
      30 	       1 	   102
      31 	       1 	   101
      32 	       1 	   100
      33 	       1 	    99
      34 	       1 	    97
      35 	       1 	    96
      36 	       1 	    95
      38 	       2 	    93
      40 	       2 	    92
      42 	       2 	    90
      44 	       2 	    88
      46 	       1 	    87
      48 	       1 	    86
      50 	       1 	    84
      52 	       1 	    83
      54 	       1 	    82
      56 	       1 	    81
      59 	       1 	    80
      62 	       1 	    78
      65 	       1 	    77
      68 	       1 	    76
      71 	       1 	    75
      74 	       1 	    74
      78 	       1 	    73
      82 	       1 	    71
      86 	       1 	    70
      90 	       1 	    69
      95 	       1 	    68
     100 	       1 	    67
     105 	       1 	    66
     111 	       1 	    65
     117 	       1 	    64
     124 	       1 	    63
     131 	       1 	    62
     139 	       1 	    60
     147 	       1 	    59
     156 	       1 	    58
     166 	       1 	    57
     177 	       1 	    56
     189 	       1 	    55
     202 	       1 	    54
     216 	       1 	    53
     231 	       1 	    52
     247 	       1 	    51
     265 	       1 	    50
     285 	       1 	    49
     307 	       1 	    48
     331 	       1 	    47
     358 	       1 	    46
     388 	       1 	    45
     421 	       1 	    44
     458 	       1 	    43
     499 	       1 	    42
     545 	       1 	    41
     597 	       1 	    40
     655 	       1 	    39
     721 	       1 	    38
     796 	       1 	    37
     881 	       1 	    36
     978 	       1 	    35
    1090 	       1 	    34
    1219 	       1 	    33
    1368 	       1 	    32
    1542 	       1 	    31
    1746 	       1 	    30
    1986 	       1 	    29
    2270 	       1 	    28
    2608 	       1 	    27
    3013 	       1 	    26
    3502 	       1 	    25
    4098 	       1 	    24
    4830 	       1 	    23
    5737 	       1 	    22
    6873 	       1 	    21
    8312 	       1 	    20
   10157 	       1 	    19
   12555 	       1 	    18
   15719 	       1 	    17
   19967 	       1 	    16
   25780 	       1 	    15
   33911 	       1 	    14
   45574 	       1 	    13
   62798 	       1 	    12
   89119 	       1 	    11
  131011 	       1 	    10
  201051 	       1 	     9
  325498 	       1 	     8
  564342 	       1 	     7
 1071481 	       1 	     6
 2308074 	       1 	     5
 5996970 	       1 	     4
21202243 	       1 	     3
136998728 	       1 	     2

One can see that moving from pixel 12 to 11 near alfa needs 27 000 iterations. Computing points up to 1 pixel near alfa needs : 2m1.236s

Drawing dynamic external ray using inverse Boettcher map by Curtis McMullen

Julia set with external rays using McMullen method

This method is based on C program by Curtis McMullen^[31] and its Pascal version by Matjaz Erat^[32]

There are 2 planes^[33] here :

w-plane ( or f0 plane )
z-plane ( dynamic plane of fc plane )

Method consist of 3 big steps :

compute some w-points of external ray of circle for angle $\theta \,$ and various radii (rasterisation)

w_{0}=R*e^{2\pi it}\,

where

1<R<\infty \,

map w-points to z-point using inverse Boettcher map $\Psi _{c}=\Phi _{c}^{-1}\,$

z_{0}=\Psi _{c}(w_{0})=f_{c}^{-n}(w_{0}^{2^{n}})\,

draw z-points ( and connect them using segments ( line segment is a part of a line that is bounded by two distinct end points^[34] )

First and last steps are easy, but second is not so needs more explanation.

Rasterisation

For given external ray in $f_{0}\,$ plane each point of ray has :

constant value $t\,$ ( external angle in turns )
variable radius $R\,$

so $w\,$ points of ray are parametrised by radius $R\,$ and can be computed using exponential form of complex numbers :

w=F_{t}(R)=R*e^{2*\Pi *i*t}\,

One can go along ray using linear scale :

t:1/3; /* example value */
R_Max:4;
R_Min:1.1;
for R:R_Max step -0.5 thru R_Min do w:R*exp(2*%pi*%i*t);
/* Maxima allows non-integer values in for statement */

It gives some w points with equal distance between them.

Another method is to use nonlinera scale.

To do it we introduce floating point exponent $r\,$ such that :

R=2^{r}\,

and

w=G_{t}(r)=2^{r}*e^{2*\Pi *i*t}\,

To compute some w points of external ray in $f_{0}\,$ plane for angle $t\,$ use such Maxima code :

t:1/3; /* external angle in turns */
/* range for computing  R ; as r tends to 0 R tends to 1 */
rMax:2; /* so Rmax=2^2=4 /
rMin:0.1; /* rMin > 0   */
caution:0.93; /* positive number < 1 ; r:r*caution  gives smaller r */
r:rMax;
unless r<rMin do
( 
 r:r*caution, /* new smaller r */ 
 R:2^r, /* new smaller R */
 w:R*exp(2*%pi*%i*t) /* new point w in f0 plane */
);

In this method distance between points is not equal but inversely proportional to distance to boundary of filled Julia set.

It is good because here ray has greater curvature so curve will be more smooth.

Mapping

Mapping points from $f_{0}\,$ -plane to $f_{c}\,$ -plane consist of 4 minor steps :

forward iteration in $f_{0}\,$ plane

w_{n}=w_{0}^{2^{n}}=R^{2^{n}}*e^{2\pi i2^{n}t}\,

until $w_{n}\,$ is near infinity

abs(w_{n})>R_{limit}\,

switching plane ( from $f_{0}\,$ to $f_{c}\,$ )

z_{n}=w_{n}\,

( because here, near infinity : $w=z\,$ )

backward iteration in $f_{c}\,$ plane the same ( $n\,$ ) number of iterations
last point $z_{0}\,$ is on our external ray

1,2 and 4 minor steps are easy. Third is not.

z_{n-1}=f_{c}^{-1}(z_{n})={\sqrt {z_{n}-c}}\,

Backward iteration uses square root of complex number. It is 2-valued functions so backward iteration gives binary tree.

One can't choose good path in such tree without extre informations. To solve it we will use 2 things :

equicontinuity of basin of attraction of infinity
conjugacy between $f_{0}\,$ and $f_{c}\,$ planes

Equicontinuity of basin of attraction of infinity

Basin of attraction of infinity ( complement of filled-in Julia set) contains all points which tends to infinity under forward iteration.

$A_{f_{c}}(\infty )\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C} :f_{c}^{(k)}(z)\to \infty \ as\ k\to \infty \}.$

Infinity is superattracting fixed point and orbits of all points have similar behaviour. In other words orbits of 2 points are assumed to stay close if they are close at the beginning.

It is equicontinuity ( compare with normality).

In $f_{c}\,$ plane one can use forward orbit of previous point of ray for computing backward orbit of next point.

Detailed version of algorithm

compute first point of ray (start near infinity ang go toward Julia set )

w=2^{r}*e^{2\Pi it}\,