Truchet tiles
In information visualization and graphic design, Truchet tiles are square tiles decorated with patterns that are not rotationally symmetric. When placed in a square tiling of the plane, they can form varied patterns, and the orientation of each tile can be used to visualize information associated with the tile's position within the tiling.[1]
Truchet tiles were first described in a 1704 memoir by Sébastien Truchet entitled "Mémoire sur les combinaisons", and were popularized in 1987 by Cyril Stanley Smith.[1][2]
Variations
Contrasting triangles
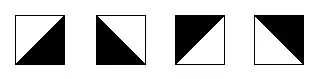
The tile originally studied by Truchet is split along the diagonal into two triangles of contrasting colors. The tile has four possible orientations.
Some examples of surface filling made tiling such a pattern.
With a scheme:

With random placement:

Quarter-circles
A second common form of the Truchet tiles, due to Smith (1987), decorates each tile with two quarter-circles connecting the midpoints of adjacent sides. Each such tile has two possible orientations.


We have such a tiling:

This type of tile has also been used in abstract strategy games Trax and the Black Path Game, prior to Smith's work.[1]
Diagonal
A labyrinth can be generated by tiles in the form of a white square with a black diagonal. As with the quarter-circle tiles, each such tile has two orientations.[3]
The connectivity of the resulting labyrinth can be analyzed mathematically using percolation theory as bond percolation at the critical point of a diagonally-oriented grid.
Nick Montfort considers the single line of Commodore 64 BASIC required to generate such patterns - 10 PRINT CHR$(205.5+RND(1)); : GOTO 10 - to be "a concrete poem, a found poem".[3]

See also
References
- Browne, Cameron (2008), "Truchet curves and surfaces", Computers & Graphics, 32 (2): 268–281, doi:10.1016/j.cag.2007.10.001.
- Smith, Cyril Stanley (1987), "The tiling patterns of Sebastian Truchet and the topology of structural hierarchy", Leonardo, 20 (4): 373–385, doi:10.2307/1578535. With a translation of Truchet's text by Pauline Boucher.
- Montfort, Nick (2012). 10 PRINT CHR$(205.5+RND(1)); : GOTO 10. MIT Press.
External links
- Weisstein, Eric W. "Truchet Tiling". MathWorld.
- Online Truchet Pattern Generator: https://truchetpatterns.netlify.app/

