45 (number)

45 as the difference of two nonzero squares (in orange).

Forty-five is the smallest odd number that has more divisors than ${\displaystyle n+1}$, and that has a larger sum of divisors than ${\displaystyle n+1}$.[1][2] It is the sixth positive integer with a square-prime prime factorization of the form ${\displaystyle p^{2}q}$, with ${\displaystyle p}$ and ${\displaystyle q}$ prime, and first of the form ${\displaystyle 3^{2}\times q}$. 45 has an aliquot sum of 33 that is part of an aliquot sequence composed of five composite numbers (45, 33, 15, 9, 4, 3, 1, and 0), all of-which are rooted in the 3-aliquot tree. This is the longest aliquot sequence for an odd number up to 45.

Forty-five is the sum of all single-digit decimal digits: ${\displaystyle 0+1+2+3+4+5+6+7+8+9=45}$. It is, equivalently, the ninth triangle number.[3]

Forty-five is also the fourth hexagonal number and the second hexadecagonal number, or 16-gonal number.[4][5] It is also the second smallest triangle number (after 1 and 10) that can be written as the sum of two squares.

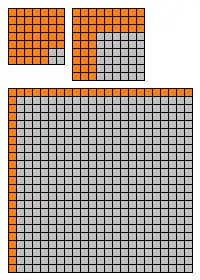
Forty-five is the smallest positive number that can be expressed as the difference of two nonzero squares in more than two ways: ${\displaystyle 7^{2}-2^{2}}$, ${\displaystyle 9^{2}-6^{2}}$ or ${\displaystyle 23^{2}-22^{2}}$ (see image).[6]

Since the greatest prime factor of ${\displaystyle 45^{2}+1=2026}$ is 1,013, which is much more than 45 twice, 45 is a Størmer number.[7] In decimal, 45 is a Kaprekar number and a Harshad number.[8][9]

Forty-five is a little Schroeder number; the next such number is 197, which is the 45th prime number.[10]

Forty-five is conjectured from Ramsey number ${\displaystyle R(5,5)}$.[11][12]

${\displaystyle \phi (45)=\phi (\sigma (45))}$[13]

• The atomic number of rhodium

45 rpm gramophone record

• A type of gramophone record classified by its rotational speed of 45 revolutions per minute (rpm)
• The group Stars on 45 and its self-titled 1981 song, "Stars on 45"
• "45 and Fat", a 1996 song by Babybird
• "Forty-Five", the title of a 2000 song by The Atomic Bitchwax
• "45", the title of a 2002 song by Elvis Costello, both referring to the 45 rpm singles and to the artist's age when he wrote the song.
• "45", the title of a 2012 song by The Gaslight Anthem
• "45", the title of a 2006 song by noodles
• "45", the title of a 2007 song by The Saturday Knights
• "45", the title of a 2003 song by Shinedown
• 45, the title of a 1982 album by Kino
• "Do the 45", the title of a 2007 song by Ryan Shaw
• forty-five is repeated continuously in the lyrics of the 1997 song "Brimful of Asha" by Cornershop

Forty-five may also refer to:

• The '45 refers to the Jacobite rising of 1745 in Great Britain, or the year that World War II ended, which was 1945.
• A card game: Forty-five.
• .45, a 2006 motion picture.
• +45 is the telephone dialing code for Denmark.
• 45, a book of essays by record producer Bill Drummond, derived both from the speed of a pop single and from his age when he finished writing it.
• A football match consists of two periods of 45 minutes each.
• Guns or ammunition of .45 caliber. In the United States, "45" is often a reference to one of two specific .45 caliber cartridges—the .45 Colt or the .45 ACP.
• The number of the French department Loiret.
• The maximum mark an International Baccalaureate student can obtain.
• In years of marriage, the sapphire wedding anniversary.
• Forty-five (audio drama), a Big Finish 2008 audio play made for the forty fifth anniversary of the British science fiction television show Doctor Who.
• Issue 45 of The North Briton was thought to be seditious but its publisher, John Wilkes, was celebrated as a champion of liberty. The number 45 was used as a symbol of support for him. Banquets were held with a theme of 45 while many items were produced showing the number or featuring it in some way. For example, a wig was produced with 45 curls.[15]
• The number of the laps of the German Grand Prix from 1978 until 2001 (except 1985 because the race was held at Nürburgring).
• Donald Trump, 45th President of the United States.

• List of highways numbered 45