Math Tutorial -- Derivatives

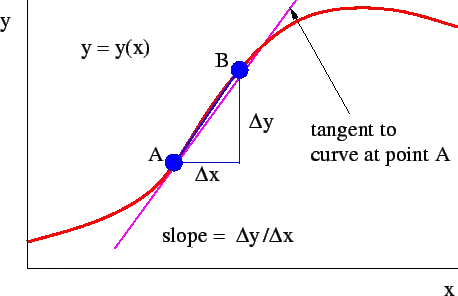
Figure 1.15: Estimation of the derivative, which is the slope of the tangent line. When point B approaches point A, the slope of the line AB approaches the slope of the tangent to the curve at point A.

This section provides a quick introduction to the idea of the derivative. For a more detailed discussion and exploration of the differentiation and of Calculus, see Calculus and Differentiation.

Often we are interested in the slope of a line tangent to a function ${\displaystyle y(x)}$ at some value of ${\displaystyle x}$. This slope is called the derivative and is denoted ${\displaystyle dy/dx}$. Since a tangent line to the function can be defined at any point ${\displaystyle x}$, the derivative itself is a function of ${\displaystyle x}$:

${\displaystyle g(x)={\frac {dy(x)}{dx}}.}$ (2.25)

As figure 1.15 illustrates, the slope of the tangent line at some point on the function may be approximated by the slope of a line connecting two points, A and B, set a finite distance apart on the curve:

${\displaystyle {\frac {dy}{dx}}\approx {\frac {\Delta y}{\Delta x}}.}$ (2.26)

As B is moved closer to A, the approximation becomes better. In the limit when B moves infinitely close to A, it is exact.

Table of Derivatives

Derivatives of some common functions are now given. In each case ${\displaystyle c}$ is a constant.

Table of Derivatives
${\displaystyle {d \over dx}c=0}$
${\displaystyle {d \over dx}x=1}$
${\displaystyle {d \over dx}cx=c}$
${\displaystyle {d \over dx}|x|={x \over |x|}=\operatorname {sgn} x,\qquad x\neq 0}$
${\displaystyle {d \over dx}x^{c}=cx^{c-1}}$	where both xc and cxc-1 are defined.
${\displaystyle {d \over dx}\left({1 \over x}\right)={d \over dx}\left(x^{-1}\right)=-x^{-2}=-{1 \over x^{2}}}$
${\displaystyle {d \over dx}\left({1 \over x^{c}}\right)={d \over dx}\left(x^{-c}\right)=-{c \over x^{c+1}}}$
${\displaystyle {d \over dx}{\sqrt {x}}={d \over dx}x^{1 \over 2}={1 \over 2}x^{-{1 \over 2}}={1 \over 2{\sqrt {x}}}}$	x > 0
${\displaystyle {d \over dx}c^{x}={c^{x}\ln c}}$	c > 0</math>
${\displaystyle {d \over dx}e^{x}=e^{x}}$
${\displaystyle {d \over dx}\log _{c}x={1 \over x\ln c}}$	c > 0, ${\displaystyle c\neq 1}$
${\displaystyle {d \over dx}\ln x={1 \over x}}$
${\displaystyle {d \over dx}\sin x=\cos x}$
${\displaystyle {d \over dx}\cos x=-\sin x}$
${\displaystyle {d \over dx}\tan x=\sec ^{2}x}$
${\displaystyle {d \over dx}\sec x=\tan x\sec x}$
${\displaystyle {d \over dx}\cot x=-\csc ^{2}x}$
${\displaystyle {d \over dx}\csc x=-\csc x\cot x}$
${\displaystyle {d \over dx}\arcsin x={1 \over {\sqrt {1-x^{2}}}}}$
${\displaystyle {d \over dx}\arccos x={-1 \over {\sqrt {1-x^{2}}}}}$
${\displaystyle {d \over dx}\arctan x={1 \over 1+x^{2}}}$
${\displaystyle {d \over dx}\operatorname {arcsec} x={1 \over |x|{\sqrt {x^{2}-1}}}}$
${\displaystyle {d \over dx}\operatorname {arccot} x={-1 \over 1+x^{2}}}$
${\displaystyle {d \over dx}\operatorname {arccsc} x={-1 \over |x|{\sqrt {x^{2}-1}}}}$
${\displaystyle {d \over dx}\sinh x=\cosh x}$
${\displaystyle {d \over dx}\cosh x=\sinh x}$
${\displaystyle {d \over dx}\tanh x={\mbox{sech}}^{2}x}$
${\displaystyle {d \over dx}{\mbox{sech}}x=-\tanh x{\mbox{sech}}x}$
${\displaystyle {d \over dx}{\mbox{coth}}x=-{\mbox{csch}}^{2}x}$
${\displaystyle {d \over dx}{\mbox{csch}}x=-{\mbox{coth}}x{\mbox{csch}}x}$
${\displaystyle {d \over dx}{\mbox{arcsinh}}x={1 \over {\sqrt {x^{2}+1}}}}$
${\displaystyle {d \over dx}{\mbox{arccosh}}x={1 \over {\sqrt {x^{2}-1}}}}$
${\displaystyle {d \over dx}{\mbox{arctanh}}x={1 \over 1-x^{2}}}$
${\displaystyle {d \over dx}{\mbox{arcsech}}x={1 \over x{\sqrt {1-x^{2}}}}}$
${\displaystyle {d \over dx}{\mbox{arccoth}}x={1 \over 1-x^{2}}}$
${\displaystyle {d \over dx}{\mbox{arccsch}}x={-1 \over |x|{\sqrt {1+x^{2}}}}}$

The product and chain rules are used to compute the derivatives of complex functions. For instance,

${\displaystyle {\frac {d}{dx}}(\sin(x)\cos(x))={\frac {d\sin(x)}{dx}}\cos(x)+\sin(x){\frac {d\cos(x)}{dx}}=\cos ^{2}(x)-\sin ^{2}(x)}$

and

${\displaystyle {\frac {d}{dx}}\log(\sin(x))={\frac {1}{\sin(x)}}{\frac {d\sin(x)}{dx}}={\frac {\cos(x)}{\sin(x)}}.}$