Decagonal antiprism
In geometry, the decagonal antiprism is the eighth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.
| Uniform decagonal antiprism | |
|---|---|
 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 22, E = 40 V = 20 (χ = 2) |
| Faces by sides | 20{3}+2{10} |
| Schläfli symbol | s{2,20} sr{2,10} |
| Wythoff symbol | | 2 2 10 |
| Coxeter diagram | |
| Symmetry group | D10d, [2+,20], (2*10), order 40 |
| Rotation group | D10, [10,2]+, (10.2.2), order 20 |
| References | U77(h) |
| Dual | Decagonal trapezohedron |
| Properties | convex |
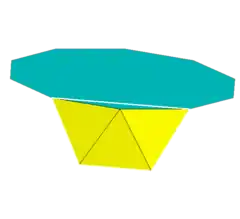 Vertex figure 3.3.3.10 | |
Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.
In the case of a regular 10-sided base, one usually considers the case where its copy is twisted by an angle 180°/n. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.
If faces are all regular, it is a semiregular polyhedron.
See also
| Antiprism name | Digonal antiprism | (Trigonal) Triangular antiprism |
(Tetragonal) Square antiprism |
Pentagonal antiprism | Hexagonal antiprism | Heptagonal antiprism | Octagonal antiprism | Enneagonal antiprism | Decagonal antiprism | Hendecagonal antiprism | Dodecagonal antiprism | ... | Apeirogonal antiprism |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | ... | ||||||||||||
| Spherical tiling image | Plane tiling image | ||||||||||||
| Vertex config. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 |
External links
- Weisstein, Eric W. "Antiprism". MathWorld.
- Decagonal Antiprism: 3-d polyhedron model
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- polyhedronisme A10
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.