Arbia's law of geography
Arbia’s law of geography states, "Everything is related to everything else, but things observed at a coarse spatial resolution are more related than things observed at a finer resolution."[1][2][3][4][5] Originally proposed as the 2nd law of geography, this is one of several laws competing for that title.[1][2][3] Because of this, Arbia's law is sometimes referred to as the second law of geography, or Arbia's second law of geography.[1][2][6][7]
Background
Since Tobler first invoked the first law of geography in his 1970s paper, there have been many attempts at a second law, including Tobler's second law of geography, and Arbia's law is one such contender.[2][5][8] Arbia's law builds on Tobler's first law of geography which states, "Everything is related to everything else, but near things tend to be more related than distant." While Tobler's first law relates to spatial autocorrelation and distance decay, Arbia's law relates to the modifiable areal unit problem, or MAUP and scale dependence of correlation.[9][10] Arbia's law was first invoked in a paper published by Giuseppe Arbia, R. Benedetti, and G. Espa titled "Effects of the MAUP on image classification," where it was presented as the second law of geography.[1] It was later referenced by Waldo Tobler in his paper "On the first law of geography: A Reply" as a possible contender for the second law of geography (this is the same paper where Tobler first proposed his second law of geography).[2] The laws of geography need not be numbered, however.[8]
Foundation
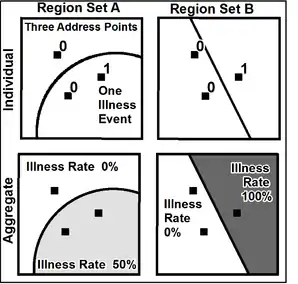
In spatial analysis with geographic information systems, both raster and vector data are used. Importantly, when working with spatially aggregate data (either in vector or raster) at a coarse resolution, it is impossible to make assumptions about what that data looks like at a finer resolution. Doing so would commit the ecological fallacy. Aggregating data spatially has a statistical smoothing effect due to the scale effect.[11]
Raster
Arbia's law was first invoked when working with raster datasets.[1] Arbia's law is important to remember when working with raster data, particularly remote sensing, where the electromagnetic spectrum is sampled at a pixel level.[12] Spatial resolution in remote sensing is related to the smallest pixel size within an image, and one value is returned for the area within a pixel. The coarser the image resolution (the larger the pixel) in a remotely sensed image, the larger the area that will be represented with the same value. Thus, a coarse resolution has a soothing effect on the image, making land cover appear more homogenous than an image with a fine spatial resolution.[1][2][13]

Vector
When working with vector datasets, the same effect is present as in Raster. With Vector datasets in GIS, it is often necessary to aggregate data into discreet spatial enumeration units (often referred to as aerial units), such as county boundaries or national borders.[14][15] The Modifiable Areal Unit Problem, or MAUP, arises from the countless possible ways to divide up the same area of land.[14][15] Dividing the land differently may produce different statistical results from the same underlying dataset, an example of which can be found in Simpson's paradox. How land is aggregated can affect the results or analysis, an effect that has been exploited by politicians through the process of gerrymandering. Arbia's law applies not just to how data are aggregated spatially but to the size of the aerial units. The larger these aerial units, the more homogenous the underlying data will appear. The same area may not appear very homogenous when the aerial units are smaller.
Controversy
In general, some dispute the entire concept of scientific laws in geography and the social sciences.[2][8] These criticisms have been addressed by Tobler and others.[2][8] However, this is an ongoing source of debate in geography and is unlikely to be resolved anytime soon.
Other Proposed Second Laws of Geography
Some have argued that geographic laws do not need to be numbered. However, the existence of a first invites the creation of a second.[5] In addition to Arbia, several scholars have proposed candidates for a second.
- Tobler's second law of geography, "the phenomenon external to a geographic area of interest affects what goes on inside," is probably the most widely accepted.[2]
- Tim Foresman and Ruth Luscombe's Second law of geography: "Things that know where they are can act on their locational knowledge. Spatially enabled things have increased financial and functional utility."
- the uncertainty principle: "that the geographic world is infinitely complex and that any representation must therefore contain elements of uncertainty, that many definitions used in acquiring geographic data contain elements of vagueness, and that it is impossible to measure location on the Earth's surface exactly."[8]
- It has been proposed that Tobler's first law of geography should be moved to the second and replaced with another.[8]
See also
- Concepts and Techniques in Modern Geography
- Boundary problem
- Cartography
- Geographic information science
- Human geography
- Indicators of spatial association
- Level of analysis
- Modifiable temporal unit problem
- Moran's I
- Physical geography
- Spatial heterogeneity
- Technical geography
- Uncertain geographic context problem
References
- Arbia, Giuseppe; Benedetti, R.; Espa, G. (1996). ""Effects of MAUP on image classification"". Journal of Geographical Systems. 3: 123–141.
- Tobler, Waldo (2004). "On the First Law of Geography: A Reply". Annals of the Association of American Geographers. 94 (2): 304–310. doi:10.1111/j.1467-8306.2004.09402009.x. S2CID 33201684. Retrieved 10 March 2022.
- Smith, Peter (2005). "The laws of geography". Teaching Geography. 30 (3): 150.
- Otto, Philipp; Dogan, Osman; Taspınar, Suleyman (November 8, 2022). "A Dynamic Spatiotemporal Stochastic Volatility Model with an Application to Environmental Risks". arXiv:2211.03178 [stat.ME].
- Hecht, Brent; Moxley, Emily (2009). "Terabytes of Tobler: Evaluating the First Law in a Massive, Domain-Neutral Representation of World Knowledge". Spatial Information Theory 9th International Conference, COSIT 2009, Aber Wrac'h, France, September 21–25, 2009, Proceedings. Lecture Notes in Computer Science. Springer. 5756: 88. Bibcode:2009LNCS.5756...88H. doi:10.1007/978-3-642-03832-7_6. ISBN 978-3-642-03831-0.
- Amdaoud, Mounir; Arcur, Giuseppe; Levratto, Nadine; Succurro, Marianna; Costanzo, Damiana (2020). "Geography of COVID-19 outbreak and first policy answers in European regions and cities".
{{cite journal}}: Cite journal requires|journal=(help) - Zhang, Boen; Xu, Gang; Jiao, Limin; Liu, Jiafeng (January 2019). "The scale effects of the spatial autocorrelation measurement: aggregation level and spatial resolution January 2019 International J". International Journal of Geographical Information Science. 33 (5): 1–22. doi:10.1080/13658816.2018.1564316. S2CID 68155432. Retrieved 6 January 2023.
- Goodchild, Michael (2004). "The Validity and Usefulness of Laws in Geographic Information Science and Geography". Annals of the Association of American Geographers. 94 (2): 300–303. doi:10.1111/j.1467-8306.2004.09402008.x. S2CID 17912938.
- Wu, Jianguo (2004). "Effects of changing scale on landscape pattern analysis: scaling relations" (PDF). Landscape Ecology. 19 (2): 125–138. doi:10.1023/B:LAND.0000021711.40074.ae. S2CID 16977988.
- Taylor, Peter (1983). Distance Decay in Spatial Interactions (PDF). ISBN 0-86094-090-X.
- Doignon, Yoann; Oliveau, Sébastien (2015). "Territorial grids in the Mediterranean: space versus population". Bollettino dell'Associazione Italiana di Cartografia. 154: 46–63. doi:10.13137/2282-472X/11827.
- Jensen, John (2016). Introductory digital image processing: a remote sensing perspective. Glenview, IL: Pearson Education, Inc. p. 623. ISBN 978-0-13-405816-0.
- Tobler, Waldo (1969). "Geographical filters and their inverses". Geographical Analysis. 1 (3): 234–53. doi:10.1111/j.1538-4632.1969.tb00621.x.
- Openshaw, Stan (1983). The Modifiable Areal Unit Problem (PDF). ISBN 0-86094-134-5.
- Chen, Xiang; Ye, Xinyue; Widener, Michael J.; Delmelle, Eric; Kwan, Mei-Po; Shannon, Jerry; Racine, Racine F.; Adams, Aaron; Liang, Lu; Peng, Jia (27 December 2022). "A systematic review of the modifiable areal unit problem (MAUP) in community food environmental research". Urban Informatics. 1. doi:10.1007/s44212-022-00021-1. S2CID 255206315. Retrieved 27 December 2022.