Alphamagic square

An alphamagic square is a magic square that remains magic when its numbers are replaced by the number of letters occurring in the name of each number. Hence 3 would be replaced by 5, the number of letters in "three". Since different languages will have a different number of letters for the spelling of the same number, alphamagic squares are language-dependent.[1] Alphamagic squares were invented by Lee Sallows in 1986.[2][3]

Example

The example below is alphamagic. To find out if a magic square is also an alphamagic square, convert it into the array of corresponding number words. For example,

52218
28152
12825

converts to ...

fivetwenty-twoeighteen
twenty-eightfifteentwo
twelveeighttwenty-five

Counting the letters in each number word generates the following square which turns out to also be magic:

498
1173
6510

If the generated array is also a magic square, the original square is alphamagic. In 2017 British computer scientist Chris Patuzzo discovered several doubly alphamagic squares in which the generated square is in turn an alphamagic square.[4]

The above example enjoys another special property: the nine numbers in the lower square are consecutive. This prompted Martin Gardner to describe it as "Surely the most fantastic magic square ever discovered."[5]

A geometric alphamagic square
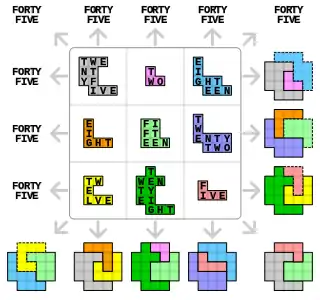
Figure 1:   A geomagic square that is also alphamagic

Sallows has produced a still more magical version—a square which is both geomagic and alphamagic. In the square shown in Figure 1, any three shapes in a straight line—including the diagonals—tile the cross; thus the square is geomagic. The number of letters in the number names printed on any three shapes in a straight line sum to forty five; thus the square is alphamagic.

Other languages

The Universal Book of Mathematics provides the following information about Alphamagic Squares:[6][7]

A surprisingly large number of 3 × 3 alphamagic squares exist—in English and in other languages. French allows just one 3 × 3 alphamagic square involving numbers up to 200, but a further 255 squares if the size of the entries is increased to 300. For entries less than 100, none occurs in Danish or in Latin, but there are 6 in Dutch, 13 in Finnish, and an incredible 221 in German. Yet to be determined is whether a 3 × 3 square exists from which a magic square can be derived that, in turn, yields a third magic square—a magic triplet. Also unknown is the number of 4 × 4 and 5 × 5 language-dependent alphamagic squares.

In 2018, the first 3 × 3 Russian alphamagic square was found by Jamal Senjaya. Following that, another 158 3 × 3 Russian alphamagic squares were found (by the same person) where the entries do not exceed 300.

References
  1. Wolfram MathWorld: Alphamagic Squares
  2. Mathematical Recreations: Alphamagic Square by Ian Stewart, Scientific American: , January 1997, pp. 106-110
  3. ACM Digital Library, Volume 4 Issue 1, Fall 1986
  4. Double Alphamagic Squares Futility Closet, November 16, 2015
  5. Gardner, Martin (1968), A Gardner's Workout: Training the Mind and Entertaining the Spirit, p. 161, A K Peters/CRC Press, Natick, Mass., July 2001, ISBN 1568811209
  6. The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, by David Darling, p. 12, Hoboken, NJ: Wiley, 2004, ISBN 0471270474
  7. "Encyclopedia of Science, Games & Puzzles: Alphamagic Squares". Archived from the original on 2017-10-10. Retrieved 2012-07-25.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.