| ←Applications of Derivatives | Real_Analysis Riemann integration |
Fundamental Theorem of Calculus→ |
Definition
Riemann integration is the formulation of integration most people think of if they ever think about integration. It is the only type of integration considered in most calculus classes; many other forms of integration, notably Lebesgue integrals, are extensions of Riemann integrals to larger classes of functions. The Riemann integral was developed by Bernhard Riemann in 1854 and was, when invented, the first rigorous definition of integration applicable to not necessarily continuous functions.
We will first define some preliminary ideas.
Partitions
Definition
Let
A Partition is defined as the ordered -tuple of real numbers such that
Norm of a Partition
Let be a partition given by
Then, the Norm (or the "mesh") of is defined as
Tagged Partition
Let be a partition
A Tagged Partition is defined as the set of ordered pairs such that . The points are called Tags.
Riemann
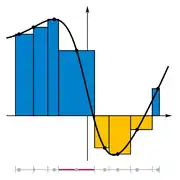
Riemann Sums
Let
Let be a tagged partition of
The Riemann Sum of over with respect to is given by
Riemann Integral
Let
Let
We say that is Integrable on if and only if, for every there exists such that for every partition satisfying , we have that
is said to be the integral of over , and is written as
or as
Properties
Theorem (Uniqueness)
Let be integrable on
Then the integral of is unique
Proof
Assume, if possible that are both integrals of over . Consider
As are integrals, there exist such that for all that satisfy and for all that satisfy
Let . Hence, if is a partition satisfying , then we have and that
That is, , which is an obvious contradiction. Hence the integral of is unique.
We now state (without proof) two seemingly obvious properties of the integral.
Theorem
Let be integrable and let
Then:
(i)
(ii)
Theorem (Boundedness Theorem)
Let be Riemann integrable. Then is bounded over
Proof
Assume if possible that is unbounded. For every divide the interval into parts. Hence, for every , is unbounded on at least one of these parts. Call it .
Now, let be given. Consider an arbitrary . Let be a tagged partition such that and , where is taken so as to satisfy .
Thus we have that . But as is arbitrary, we have a contradiction to the fact that is Riemann integrable.
Hence, is bounded.
Integrability
We now study classes of Riemann integrable functions. The first "constraint" on Riemann integrable functions is provided by the Cauchy Integrability Criterion.
Theorem (Cauchy Criterion)
Let
Then,
(i) is Riemann integrable on if and only if
(ii) For every , there exists such that if are two partitions satisfying then
Proof
()Let and let be given.
Then, there exists such that for every partition satisfying ,we have
Now, let partitions be such that .
Thus we have that , that is
() For every , consider such that for all partitions satisfying , we have .
Without loss of generality, we can assume that when . For every , let be a partition such that
The sequence is a Cauchy sequence, and hence it has a limit .
Now, for every , we have a such that implies .
Thus
Theorem (Squeeze Theorem)
Let
Then,
(i) is Riemann integrable on if and only if
(ii) For every , there exist Riemann integrable functions such that
for all and
Proof
()Take . It is easy to see that
()Let . Then, there exist functions such that . Further, if and , then there exist such that if a partition satisfies then and then
Now let be a partition satisfying .
Now, we can easily see that . Hence, is a Cauchy sequence, with a limit , and as in the previous proof, we can show that