< Calculus
The definite integral of a function f(x) from x=0 to x=a is equal to the area under the curve from 0 to a.

Basics of Integration

4.1 Definite integral

4.2 Fundamental Theorem of Calculus

4.3 Indefinite integral

4.4 Improper Integrals

Integration Techniques

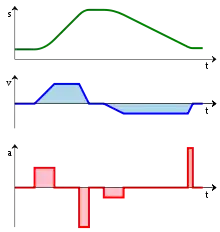
From bottom to top:
  • an acceleration function a(t);
  • the integral of the acceleration is the velocity function v(t);
  • and the integral of the velocity is the distance function s(t).

4.5 Infinite Sums

4.6 Derivative Rules and the Substitution Rule

4.7 Integration by Parts

4.8 Trigonometric Substitutions

4.9 Trigonometric Integrals

4.10 Rational Functions by Partial Fraction Decomposition

4.11 Tangent Half Angle Substitution

4.12 Reduction Formula

4.13 Irrational Functions

4.14 Numerical Approximations

4.15 Exercises

Applications of Integration

4.16 Area

4.17 Volume

4.18 Volume of Solids of Revolution

4.19 Arc Length

4.20 Surface Area

4.21 Work

4.22 Center of Mass

4.23 Pressure and Force

4.24 Probability

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.