Secant

The secant of an angle is the reciprocal of its cosine.

${\displaystyle \sec x={\frac {1}{\cos x}}}$

Cosecant

The cosecant of an angle is the reciprocal of its sine.

${\displaystyle \operatorname {cosec} x={\frac {1}{\sin x}}}$ ^{[note 1]}

Cotangent

The cotangent of an angle is the reciprocal of its tangent.

${\displaystyle \cot x={\frac {1}{\tan x}}}$

Graphs

• 
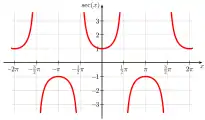  Graph of sec x
• 
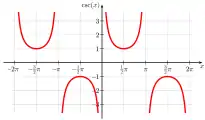  Graph of cosec x
• 
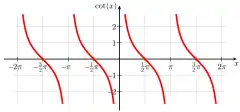  Graph of cot x

Solving Equations with Secants, Cosecants, and Cotangents

Solving an equation with secants, cosecants, or cotangents is pretty much the same method as with any other trigonometric equation.

e.g. Solve ${\displaystyle -\sec x=2+\cos x}$ for ${\displaystyle 0<x<2\pi }$

${\displaystyle {\begin{aligned}-\sec x&=2+\cos x\\-1&=2\cos x+\cos ^{2}x\\\cos ^{2}x+2\cos x+1&=0\\(\cos x+1)^{2}&=0\\\cos x+1&=0\\\cos x&=-1\\x&=\pi \end{aligned}}}$

Cotangent identity

${\displaystyle \tan x\equiv {\frac {\sin x}{\cos x}}}$ and ${\displaystyle \cot x\equiv {\frac {1}{\tan x}}}$, therefore ${\displaystyle \cot x\equiv {\frac {\cos x}{\sin x}}}$

Pythagorean-derived identities

The Pythagorean trigonometric identity states that ${\displaystyle \sin ^{2}x+\cos ^{2}x\equiv 1}$. We can divide both sides by ${\displaystyle \cos ^{2}x}$ to obtain another identity: ${\displaystyle \tan ^{2}x+1\equiv \sec ^{2}x}$. Alternatively, we can divide both sides by ${\displaystyle \sin ^{2}x}$ to obtain ${\displaystyle 1+\cot x\equiv \operatorname {cosec} x}$.

Double Angle Formulae

The double angle formulae are a special case of the addition formulae, when both of the terms in the sum are equal.

${\displaystyle {\begin{aligned}\sin(2A)&=\sin(A+A)=\sin A\cos A+\sin A\cos A=2\sin A\cos A\\\cos(2A)&=\cos(A+A)=\cos A\cos A-\sin A\sin A=\cos ^{2}A-\sin ^{2}A=2\cos ^{2}A-1=1-2\sin ^{2}A\\\tan(2A)&=\tan(A+A)={\frac {\tan A+\tan A}{1-\tan A\tan A}}={\frac {2\tan A}{1-\tan ^{2}A}}\end{aligned}}}$

Converting ${\displaystyle a\sin \theta +b\cos \theta }$ to ${\displaystyle R\sin(\theta \pm \alpha )}$ or ${\displaystyle R\cos(\theta \pm \alpha )}$

It is helpful when solving trigonometric equations to convert an expression into a single term. To do this, we can use the addition formulae.

e.g. Solve ${\displaystyle \sin \theta +{\sqrt {3}}\cos \theta =1}$ for ${\displaystyle 0<\theta <2\pi }$

${\displaystyle {\begin{aligned}\sin \theta +{\sqrt {3}}\cos \theta &=R\sin(\theta +\alpha )\\\sin \theta +{\sqrt {3}}\cos \theta &=R\sin \theta \cos \alpha +R\cos \theta \sin \alpha \\{\text{Equate coefficients of }}\sin \theta \to \quad R\cos \alpha &=1\\{\text{Equate coefficients of }}\cos \theta \to \quad R\sin \alpha &={\sqrt {3}}\\\tan \alpha &={\frac {R\sin \alpha }{R\cos \alpha }}={\frac {\sqrt {3}}{1}}\\\therefore \alpha &={\frac {\pi }{3}}\\R\cos({\frac {\pi }{3}})&=1\\R&={\frac {1}{\tfrac {1}{2}}}=2\\2\sin(\theta +{\frac {\pi }{3}})&=1\\\sin(\theta +{\frac {\pi }{3}})&={\frac {1}{2}}\\\theta +{\frac {\pi }{3}}&=\left\{{\frac {5\pi }{6}},{\frac {13\pi }{6}}\right\}\leftarrow {\text{Be careful with the domain of }}\theta +{\frac {\pi }{3}}\\\theta &=\left\{{\frac {3\pi }{6}},{\frac {11\pi }{6}}\right\}\end{aligned}}}$

Using ${\displaystyle R\cos(\theta \pm \alpha )}$ is pretty similar.

e.g. Solve ${\displaystyle {\sqrt {2}}\sin \theta +{\sqrt {2}}\cos \theta =1}$ for ${\displaystyle 0<\theta <2\pi }$

${\displaystyle {\begin{aligned}{\sqrt {2}}\sin \theta +{\sqrt {2}}\cos \theta &=R\cos(\theta -\alpha )\\{\sqrt {2}}\sin \theta +{\sqrt {2}}\cos \theta &=R\cos \theta \cos \alpha +R\sin \theta \sin \alpha \\{\text{Equate coefficients of}}\sin \theta \to \quad R\sin \alpha &={\sqrt {2}}\\{\text{Equate coefficients of}}\cos \theta \to \quad R\cos \alpha &={\sqrt {2}}\\\tan \alpha &={\frac {R\sin \alpha }{R\cos \alpha }}={\frac {\sqrt {2}}{\sqrt {2}}}=1\\\therefore \alpha &={\frac {\pi }{4}}\\R\sin \left({\frac {\pi }{4}}\right)&={\sqrt {2}}\\R\left({\frac {1}{\sqrt {2}}}\right)&={\sqrt {2}}\\R&={\sqrt {2}}({\sqrt {2}})=2\\2\cos(\theta -{\frac {\pi }{4}})&=1\\\cos(\theta -{\frac {\pi }{4}})&={\frac {1}{2}}\\\theta -{\frac {\pi }{4}}&=\left\{{\frac {\pi }{3}},{\frac {5\pi }{3}}\right\}\\\theta &=\left\{{\frac {7\pi }{12}},{\frac {23\pi }{12}}\right\}\end{aligned}}}$

Notes

1. ↑ Some sources may use ${\displaystyle \csc x}$, but this notation is not endorsed by Cambridge
2. ↑ The proofs of these formulae are beyond the scope of the Cambridge Syllabus, but you can read about the proofs at Wikipedia