A-level Mathematics/CIE/Pure Mathematics 2/Algebra

The Modulus Function

The modulus function^{[note 1]} $|x|$ returns the magnitude of $x$ . For instance, $|\!-\!3|$ will return $3$ , $|5|$ will return $5$ .

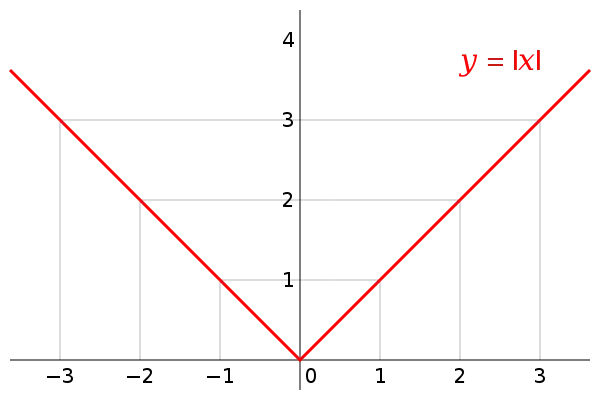
The modulus function can be defined as $|x|={\begin{cases}-x,&{\text{if }}x<0\\x,&{\text{if }}x\geq 0\end{cases}}$ .

The modulus function as a graph.

Graphing the modulus function

Graphs of the modulus function are just a straight-line graph that has been reflected for negative output values. The graph of $y=|ax+b|$ is like the graph of $y=ax+b$ except that every point below the x-axis folds upwards to produce a V-shaped graph.

Here is an interactive graph which shows the relationship between the graph of a line and the graph of the modulus of that line.

Solving Equations & Inequalities

To solve equations and inequalities involving the modulus function, we can square both sides.

e.g. Solve $|4x+2|>|2x-3|$

${\begin{aligned}|4x+2|&>|2x-3|\\(4x+2)^{2}&>(2x-3)^{2}\\16x^{2}+16x+4&>4x^{2}-12x+9\\12x^{2}+28x-5&>0\\x^{2}+{\frac {7}{3}}x&>{\frac {5}{12}}\\(x+{\frac {7}{6}})^{2}&>{\frac {15}{36}}+{\frac {49}{36}}\\x+{\frac {7}{6}}>{\sqrt {\frac {64}{36}}}&{\text{ or }}x+{\frac {7}{6}}<-{\sqrt {\frac {64}{36}}}\\x+{\frac {7}{6}}>{\frac {8}{6}}&{\text{ or }}x+{\frac {7}{6}}<-{\frac {8}{6}}\\x>{\frac {1}{6}}&{\text{ or }}x<-{\frac {15}{6}}\\{\text{In interval notation, }}x&\in \left(-\infty ,-{\tfrac {5}{2}}\right)\cup \left({\tfrac {1}{6}},\infty \right)\end{aligned}}$

An alternative method is to look at the places where the functions inside the modulus change sign, i.e. where $f(x)=0$ .

$4x+2$ changes sign at $x=-{\frac {1}{2}}$

$2x-3$ changes sign at $x={\frac {3}{2}}$

${\begin{array}{ccc}{\text{Where }}x<-{\frac {1}{2}}&{\text{Where }}-\!{\frac {1}{2}}\leq x<{\frac {3}{2}}&{\text{Where }}{\frac {3}{2}}\leq x\\-(4x+2)>-(2x-3)&4x+2>-(2x-3)&4x+2>2x-3\\4x+2<2x-3&4x+2>-2x+3&4x+2>2x-3\\2x<-5&6x>1&2x>-5\\x<-{\frac {5}{2}}&x>{\frac {1}{6}}&x>-{\frac {5}{2}}\\&&{\text{Out of range}}\\\end{array}}$

${\text{In interval notation, }}x\in \left(-\infty ,-{\tfrac {5}{2}}\right)\cup \left({\tfrac {1}{6}},\infty \right)$

Dividing Polynomials

Dividing polynomials uses the same method as dividing numbers with long division.

Dividing Numbers

Suppose we need to find $22253\div 17$ . We can use the method of long division:

  ______
17|22253

  __1___
17|22253  17 goes into 22 once with 5 left over
  -17↓    
    52    Next we bring down the 2
    
  __13__
17|22253  
  -17↓↓
    52↓   17 goes into 52 thrice with 1 left over
   -51↓
     15   Next we bring down the 5
    
  __1309
17|22253  
  -17↓↓↓  17 doesn't go into 15, so we bring down the 3
    52↓↓
   -51↓↓
     153  17 goes into 153 nine times with nothing left over
    -153
       0

Thus, $22253\div 17=1309$

Dividing Polynomials

We can use the same method to divide polynomials.

e.g. $(x^{3}+2x^{2}+2x+1)\div (x+1)$

      ____________________
x + 1 |x^3 + 2x^2 + 2x + 1

      ________x^2_________
x + 1 |x^3 + 2x^2 + 2x + 1    (x + 1) goes into (x^3 + 2x^2) x^2 times with x^2 left over
     -(x^3 +  x^2)   ↓
              x^2 + 2x         Bring down the 2x

      ________x^2_+__x____
x + 1 |x^3 + 2x^2 + 2x + 1    (x + 1) goes into (x^2 + 2x) x times with x left over
     -(x^3 +  x^2)   ↓   ↓
              x^2 + 2x   ↓     Bring down the 1
            -(x^2 +  x)  ↓
                     x + 1

      ________x^2_+__x___1
x + 1 |x^3 + 2x^2 + 2x + 1    (x + 1) goes into (x + 1) once with nothing left over
     -(x^3 +  x^2)   ↓   ↓
              x^2 + 2x   ↓     
            -(x^2 +  x)  ↓
                     x + 1
                   -(x + 1)
                         0

Thus, $(x^{3}+2x^{2}+2x+1)\div (x+1)=x^{2}+x+1$

The Remainder Theorem

A remainder occurs when the divisor does not fit into the dividend a whole number of times.

e.g. $22256\div 17={\frac {22253}{17}}+{\frac {3}{17}}=1309+{\frac {3}{17}}$ has a remainder of $3$ .

It can also occur in polynomials:

      ____________________
x + 2 |x^3 + 3x^2 + 3x + 3

      ________x^2_________
x + 2 |x^3 + 3x^2 + 3x + 3
     -(x^3 + 2x^2)   ↓
              x^2 + 3x
              
      ________x^2_+__x____
x + 2 |x^3 + 3x^2 + 3x + 3
     -(x^3 + 2x^2)   ↓   ↓
              x^2 + 3x   ↓
            -(x^2 + 2x)  ↓
                     x + 3

      ________x^2_+__x_+_1
x + 2 |x^3 + 3x^2 + 3x + 3
     -(x^3 + 2x^2)   ↓   ↓
              x^2 + 3x   ↓
            -(x^2 + 2x)  ↓
                     x + 3
                   -(x + 2)
                         1

Here, the remainder is $1$ .

This can be expressed as $x^{3}+3x^{2}+3x+3=(x^{2}+x+1)(x+2)+1$

In general, a quotient and remainder can be expressed as $Dividend=(Quotient)(Divisor)+Remainder$

This expression leads to a useful theorem in mathematics: the remainder theorem.

If we divide a polynomial $p(x)$ by a given divisor $(ax-b)$ , the expression can be written as $p(x)=(Quotient)(ax-b)+Remainder$ .

If we substitute the value of $b/a$ into the polynomial, we get:

${\begin{aligned}p(b/a)&=(Quotient)(a(b/a)-b)+Remainder\\p(b/a)&=(Quotient)(b-b)+Remainder\\p(b/a)&=(Quotient)(0)+Remainder\\p(b/a)&=Remainder\\\end{aligned}}$

Thus, the remainder theorem states that for a given polynomial $p(x)$ , $p(b/a)$ gives the remainder obtained from ${\frac {p(x)}{ax-b}}$ .

e.g. If $p(x)=x^{3}+3x^{2}+3x+3$ , $p(-2)$ will give the remainder obtained from $(x^{3}+3x^{2}+3x+3)\div (x+2)$ :

${\begin{aligned}p(-2)&=(-2)^{3}+3(-2)^{2}+3(-2)+3\\&=-8+3(4)-6+3\\&=-8+12-3\\&=1\end{aligned}}$

The Factor Theorem

The factor theorem is a special case of the remainder theorem for when the remainder is zero.

If the remainder is zero, that means that the divisor is a factor of the dividend.

Thus, if $p(b/a)=0$ , $(ax-b)$ is a factor of $p(x)$

e.g. $p(x)=x^{3}-5x^{2}+x+10$ . Use the factor theorem to find a factor of $p(x)$ .

${\begin{aligned}p(1)&=1^{3}-5(1^{2})+1+10=1-5+1+10=7&\neq 0\\p(-1)&=(-1)^{3}-5(-1)^{2}-1+10=-1-5-1-10=-17&\neq 0\\p(2)&=2^{3}-5(2^{2})+2+10=8-5(4)+2+10=8-20+12&=0\\\therefore \ &(x-2){\text{ is a factor of }}x^{3}-5x^{2}+x+10\end{aligned}}$

Notes

↑ Also known as the absolute value function

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Also known as the absolute value function

[note 1]