Vadalog
The Vadalog system is a Knowledge Graph Management System (KGMS) that offers a language for performing complex logic reasoning tasks over knowledge graphs. At the same time, Vadalog delivers a platform to support the entire spectrum of data science tasks: data integration, pre-processing, statistical analysis, machine learning, algorithmic modeling, probabilistic reasoning and temporal reasoning.[1] Its language is based on an extension of the rule-based language Datalog, Warded Datalog±, a high-performance language using an aggressive termination control strategy.[2] Vadalog can support the entire spectrum of data science activities and tools. The system can read from and connect to multiple sources, from relational databases, such as PostgreSQL and MySQL, to graph databases, such as Neo4j, as well as make use of machine learning tools (e.g., Weka and scikit-learn), and a web data extraction tool, OXPath. Additional Python libraries and extensions can also be easily integrated into the system.[3]
| Paradigm | Logic, Declarative |
|---|---|
| Family | Datalog |
| Designed by | University of Oxford, TU Wien, Bank of Italy |
Vadalog is the result of a joint effort between University of Oxford, the Knowledge Graph Lab of Technische Universität Wien and Bank of Italy.
Knowledge graph management systems (KGMS)
A knowledge graph management system (KGMS) has to manage knowledge graphs, which incorporate large amounts of data in the form of facts and relationships. In general, it can be seen as the union of three components: [4]
- KBMS, that is, a knowledge base management system,
- Big Data, which is the need of handling large amounts of data, especially when considering that knowledge graphs have been thought as a solution for integrating multiple data sources, both corporate and public knowledge, which can be integrated into large knowledge graphs,
- (Data) Analytics is the need to provide access to existing software packages for machine learning, text mining, data analytics, and data visualization and to combine them together in the same platform.
From a more technical standpoint, some additional requirements can be identified for defining a proper KGMS:
- definition of a language and a formalism with high expressive power,[5][6]
- cost-effective data wrangling, in all its steps, from data cleaning to web data extraction and big data access from many different sources,[7]
- efficient logical, probabilistic and ontological reasoning,[8][4]
- low complexity, both in terms of space complexity (to handle big data) and syntax,
- interfaces (APIs) to access many heterogeneous data sources, such as corporate RDBMS, NoSQL or RDF stores, the web, machine-learning and analytics packages.[3]
Other requirements may include more typical DBMS functions and services, as the ones proposed by Codd.[9]
Vadalog system
Vadalog offers a platform that fulfills all the requirements of a KGMS listed above. It is able to perform rule-based reasoning tasks on top of knowledge graphs and it also supports the data science workflow, such as data visualization and machine learning.[4]
Reasoning task and recursion
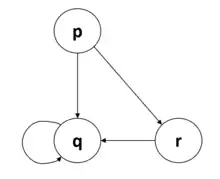
A rule is an expression of the form n :− a1, …, an where:
- a1, …, an are the atoms of the body,
- n is the atom of the head.
A rule allows to infer new knowledge starting from the variables that are in the body: when all the variables in the body of a rule are successfully assigned, the rule is activated and it results in the derivation of the head predicate: given a database D and a set of rules Σ, a reasoning task aims at inferring new knowledge, applying the rules of the set Σ to the database D (the extensional knowledge).
The most widespread form of knowledge that has been adopted over the last decades has been in the form of rules, be it in rule-based systems, ontology-based systems or other forms and it can be typically captured in knowledge graphs.[3] The nature of knowledge graphs also makes the presence of recursion in these rules a particularly important aspect. Recursion means that the same rules might be called multiple times before obtaining the final answer of the reasoning task and it is particularly powerful as it allows an inference based on previously inferred results. This implies that the system must provide a strategy that guarantees termination. More technically, a program is recursive if the dependency graph built with the application of the rules is cyclical. The simplest form of recursion is that in which the head of a rule also appears in the body (self-recursive rules).
The query language
The Vadalog language allows to answer reasoning queries that also include recursion. It is based on Warded Datalog±, which belongs to the Datalog± family of languages that extends Datalog with existential quantifiers in rule heads[10] and at the same time restricts its syntax in order to achieve decidability and tractability.[11][12] Existential rules are also known as tuple-generating dependencies (tgds).[1]
An existential rule has the following form:
or, alternatively, in Datalog syntax, it can be written as follows:
p(X,Z) :- r(X).
Variables in Vadalog are like variables in first-order logic and a variable is local to the rule in which it occurs. This means that occurrences of the same variable name in different rules refer to different variables.
Warded Datalog±
In case of a set of rules , consisting of the following:
r(X,Y) :- p(X).
p(Z) :- r(X,Z).
the variable Z in the second rule is said to be dangerous, since the first rule will generate a null in the second term of the atom r and this will be injected to the second rule to get the atom p, leading to a propagation of nulls when trying to find an answer to the program. If arbitrary propagation is allowed, reasoning is undecidable and the program will be infinite.[3] Warded Datalog± overcomes this issue asking that for every rule defined in a set , all the variables in the rule bodies must coexist in at least one atom in the head, called a ward. The concept of wardness restricts the way dangerous variable can be used inside a program. Although this is a limit in terms of expressive power, with this requirement and thanks to its architecture and termination algorithms, Warded Datalog± is able to find answers to a program in a finite number of steps. It also exhibits a good trade-off between computational complexity and expressive power, capturing PTIME data complexity while allowing ontological reasoning and the possibility of running programs with recursion.[13]
Vadalog extension
Vadalog replicates in its entirety Warded Datalog± and extends it with the inclusion in the language of:
- monotonic aggregations (min, max, sum, prod, count operators),[14]
- stratified negation,
- support for different data types (strings, integer, double, date, boolean, set, lists, marked nulls),
- rich annotation mechanism to define how to interact with data sources and external libraries.
In addition, the system provides a highly engineered architecture to allow efficient computation. This is done in the following two ways.
- Adopting an in-memory processing architecture and a pull stream-based approach, which limits the memory consumption or make it predictable.
- Using an aggressive termination control strategy, which detects patterns and redundancy while building of the chase-graph (used to generate the answers) as early as possible and cuts off computation when they occur.[3] This is connected with the concept of isomorphism of facts, which reduces the number of steps needed to get an answer: if a fact h is isomorphic to h', the system will only explore the chase graph of fact h.[15]
The Vadalog system is therefore able to perform ontological reasoning tasks, as it belongs to the Datalog family. Reasoning with the logical core of Vadalog captures OWL 2 QL and SPARQL[16] (through the use of existential quantifiers), and graph analytics (through support for recursion and aggregation). The declarative nature of the language makes the code easy-to-read and manageable.[1]
Example of ontological reasoning task
Consider the following set of Vadalog rules:
ancestor(Y,X) :- person(X).
ancestor(Y,Z) :- ancestor(Y,X), parent(X,Z).
The first rule states that for each person there exists an ancestor . The second rule states that, if is a parent of , then is an ancestor of too. Note the existential quantification in the first position of the ancestor predicate in the first rule, which will generate a null νi in the chase procedure. Such null is then propagated to the head of the second rule. Consider a database D = {person(Alice), person(Bob), parent(Alice,Bob)} with the extensional facts and the query of finding all the entailed ancestor facts as reasoning task.
By performing the chase procedure, the fact ancestor(ν1,Alice) is generated by triggering the first rule on person(Alice). Then, ancestor(ν1,Bob) is created by activating the second rule on ancestor(ν1,Alice) and parent(Alice,Bob). Finally, the first rule could be triggered on person(Bob), but the resulting fact ancestor(ν2,Bob) is isomorphic with ancestor(ν1,Bob), thus this fact is not generated and the corresponding portion of the chase graph is not explored.
In conclusion, the answer to the query is the set of facts {ancestor(ν1,Alice), ancestor(ν1,Bob)}.
Additional Features
The integration of Vadalog with data science tools is achieved by means of data bindings primitives and functions.[3]
- Data binding primitives: bindings allow to connect to external data sources or systems like a database, a framework or a library and tell the system how to deal with them. This includes connections with relational database systems as PostgreSQL or MySQL, and graph databases, such as Neo4j. It is also possible to integrate machine learning libraries (Weka, scikit-learn, Tensorflow) and a web data extraction tool, OXPath, which allows to retrieve data directly from the web. This is possible through the so-called annotations: they are special facts that augment the sets of existential rules with specific behaviours. The
@inputannotation tells the system that the facts for an atom of the program are imported from an external data source, e.g., a relational database. The@outputannotation specifies that the facts for an atom of the program will be exported to an external target, e.g., the standard output or a relational database. Other annotations like@bind,@mapping,@qbindallow to customize the data sources for the@inputannotation or the targets for the@outputannotation. - Functions: custom expressions which make use of arithmetic operators, string manipulation or comparison can also be supported. Libraries written in Python are also enabled and they can be integrated with the dedicated annotation
@library.
The system also provides an integration with the JupyterLab platform, where Vadalog programs can be written and run and the output can be read, exploiting the functionalities of the platform. It gives also the possibility to evaluate the correctness of the program, run it and analyse the derivation process of output facts by means of tools as syntax highlighting, code analysis (checking whether the code is correct or there are errors) and explanations of results (how the result has been obtained): all these functionalities are embedded in the notebook and help in writing and analyzing Vadalog code.
Use Cases
The Vadalog system can be employed to address many real-world use cases from distinct research and industry fields.[5] Among the latter, this section presents two relevant and accessible cases belonging to the financial domain.[17][18][19]
Company Control
A company ownership graph shows entities as nodes and shares as edges. When an entity has a certain amount of shares on another one (commonly identified in the absolute majority), it is able to exert a decision power on that entity and this configures a company control and, more generally, a group structure. Searching for all control relationships requires to investigate different scenarios and very complex group structures, namely direct and indirect control. This query be translated into the following rules:
- a company X directly controls a company Y if X directly owns more than 50% of the total equity of Y ,
- a company X indirectly controls a company Y if X controls a set of intermediary companies that jointly (i.e., summing their shares) own more than 50% of Y.
These rules can be written in a Vadalog program that will derive all control edges like the following:
control(X,X) :- company(X).
control(X,Y) :- control(X,Y), own(Y,Z,W), V = sum(W,<Y>), V > 0.5.
The first rule states that each company controls itself. The second rule defines control of X over Z by summing the shares of Z held by companies Y, over all companies Y controlled by X.
Close Link
This scenario consists in determining whether there exists a link between two entities in a company ownerships graph. Determining the existence of such links is relevant, for instance, in banking supervision and credit worthiness evaluation, as a company cannot act as guarantor for loans to another company if the two share such a relationship. Formally, two companies X and Y are involved in a close link if:
- x (resp., Y) owns directly or indirectly 20% or more of the equity of Y (resp., X), or
- a common third-party Z owns directly or indirectly 20% or more of the equity of both X and Y.
These rules can be written in a Vadalog program that will derive all close link edges like the following:
mcl(X,Y,S) :- own(X,Y,S).
mcl(X,Z,S1 * S2) :- mc1(X,Y,S1), own(Y,Z,S2).
cl1(X,Y) :- mcl(X,Y,S), TS = sum(S), TS > 0.2.
cl2(X,Y) :- cl1(Z,X), cl1(Z,Y), X != Y.
closelink(X,Y) :- cl1(X,Y).
closelink(X,Y) :- cl2(X,Y).
The first rule states that two companies X and Y connected by an ownership edge are possible close links. The second rule states that, if X and Y are possible close links with a share S1 and there exists an ownership edge from Y to a company Z with a share S2, then also X and Z are possible close links with a share S1 * S2. The third rule states that, if the sum of all the partial shares S of Y owned directly or indirectly by X is greater than or equal to 20% of the equity of Y, then they are close links according to the first definition. The fourth rule models the second definition of close links, i.e., the third-party case.
References
- Bellomarini, Luigi; Fayzrakhmanov, Ruslan R.; Gottlob, Georg; Kravchenko, Andrey; Laurenza, Eleonora; Nenov, Yavor; Sallinger, Emanuel; Sherkhonov, Evgeny; Vahdati, Sahar; Wu, Lianlong (2022-04-01). "Data science with Vadalog: Knowledge Graphs with machine learning and reasoning in practice". Future Generation Computer Systems. 129: 407–422. doi:10.1016/j.future.2021.10.021. ISSN 0167-739X. S2CID 243885469.
{{cite journal}}: Missing|author8=(help) - Bellomarini, Luigi; Sallinger, Emanuel; Gottlob, Georg (2018-05-01). "The Vadalog system: datalog-based reasoning for knowledge graphs". Proceedings of the VLDB Endowment. 11 (9): 975–987. doi:10.14778/3213880.3213888. ISSN 2150-8097. S2CID 49300741.
- Bellomarini, Luigi; Fayzrakhmanov, Ruslan R.; Gottlob, Georg; Kravchenko, Andrey; Laurenza, Eleonora; Nenov, Yavor; Reissfelder, Stephane; Sallinger, Emanuel; Sherkhonov, Evgeny; Wu, Lianlong (2018-07-23). "Data Science with Vadalog: Bridging Machine Learning and Reasoning". arXiv:1807.08712 [cs.DB].
- Bellomarini, Luigi; Gottlob, Georg; Pieris, Andreas; Sallinger, Emanuel (2018). "Swift Logic for Big Data and Knowledge Graphs" (PDF). In Tjoa, A Min; Bellatreche, Ladjel; Biffl, Stefan; van Leeuwen, Jan; Wiedermann, Jiří (eds.). SOFSEM 2018: Theory and Practice of Computer Science. Lecture Notes in Computer Science. Vol. 10706. Cham: Springer International Publishing. pp. 3–16. doi:10.1007/978-3-319-73117-9_1. ISBN 978-3-319-73117-9. S2CID 3193327.
- Bellomarini, Luigi; Fakhoury, Daniele; Gottlob, Georg; Sallinger, Emanuel (2019). "Knowledge Graphs and Enterprise AI: The Promise of an Enabling Technology". 2019 IEEE 35th International Conference on Data Engineering (ICDE). Macao, Macao: IEEE. pp. 26–37. doi:10.1109/ICDE.2019.00011. ISBN 978-1-5386-7474-1. S2CID 174818761.
- Dantsin, Evgeny; Eiter, Thomas; Gottlob, Georg; Voronkov, Andrei (2001-09-01). "Complexity and expressive power of logic programming". ACM Computing Surveys. 33 (3): 374–425. doi:10.1145/502807.502810. ISSN 0360-0300.
- Konstantinou, Nikolaos; Koehler, Martin; Abel, Edward; Civili, Cristina; Neumayr, Bernd; Sallinger, Emanuel; Fernandes, Alvaro A.A.; Gottlob, Georg; Keane, John A.; Libkin, Leonid; Paton, Norman W. (2017-05-09). "The VADA Architecture for Cost-Effective Data Wrangling". Proceedings of the 2017 ACM International Conference on Management of Data. SIGMOD '17. New York, NY, USA: Association for Computing Machinery. pp. 1599–1602. doi:10.1145/3035918.3058730. hdl:20.500.11820/36295a10-0b57-48a8-82ac-19d856815a89. ISBN 978-1-4503-4197-4. S2CID 11521729.
- Cali`, Andrea; Gottlob, Georg; Pieris, Andreas (2012-12-01). "Towards more expressive ontology languages: The query answering problem". Artificial Intelligence. 193: 87–128. doi:10.1016/j.artint.2012.08.002. ISSN 0004-3702.
- Connolly, Thomas M.; Begg, Carolyn E. (2014). Database Systems – A Practical Approach to Design Implementation and Management (6th ed.) (6th ed.). Pearson. ISBN 978-1292061184.
- Calì, Andrea; Gottlob, Georg; Lukasiewicz, Thomas (2012-07-01). "A general Datalog-based framework for tractable query answering over ontologies". Journal of Web Semantics. Special Issue on Dealing with the Messiness of the Web of Data. 14: 57–83. doi:10.1016/j.websem.2012.03.001. ISSN 1570-8268.
- Abiteboul, Serge; Hull, Richard; Vianu, Victor (1995). Foundations of Databases: The Logical Level (1st ed.). USA: Addison-Wesley Longman Publishing Co., Inc. ISBN 978-0-201-53771-0.
- Calì, Andrea; Gottlob, Georg; Lukasiewicz, Thomas; Marnette, Bruno; Pieris, Andreas (2010). "Datalog+/-: A Family of Logical Knowledge Representation and Query Languages for New Applications". 2010 25th Annual IEEE Symposium on Logic in Computer Science. pp. 228–242. doi:10.1109/LICS.2010.27. ISBN 978-1-4244-7588-9. S2CID 16829529.
- Bellomarini, Luigi; Benedetto, Davide; Gottlob, Georg; Sallinger, Emanuel (2022-03-01). "Vadalog: A modern architecture for automated reasoning with large knowledge graphs". Information Systems. 105: 101528. doi:10.1016/j.is.2020.101528. ISSN 0306-4379. S2CID 218964910.
- Shkapsky, Alexander; Yang, Mohan; Zaniolo, Carlo (2015). "Optimizing recursive queries with monotonic aggregates in DeALS". 2015 IEEE 31st International Conference on Data Engineering. pp. 867–878. doi:10.1109/ICDE.2015.7113340. ISBN 978-1-4799-7964-6. S2CID 5345997.
- Bellomarini, Luigi; Laurenza, Eleonora; Sallinger, Emanuel; Sherkhonov, Evgeny (2020). "Reasoning Under Uncertainty in Knowledge Graphs". In Gutiérrez-Basulto, Víctor; Kliegr, Tomáš; Soylu, Ahmet; Giese, Martin; Roman, Dumitru (eds.). Rules and Reasoning. Lecture Notes in Computer Science. Vol. 12173. Cham: Springer International Publishing. pp. 131–139. doi:10.1007/978-3-030-57977-7_9. ISBN 978-3-030-57977-7. S2CID 221193385.
- Gottlob, G.; Pieris, Andreas (2015). "Beyond SPARQL under OWL 2 QL Entailment Regime: Rules to the Rescue". IJCAI. S2CID 6980701.
- Atzeni, Paolo; Bellomarini, Luigi; Iezzi, Michela; Sallinger, Emanuel; Vlad, Adriano. "Weaving Enterprise Knowledge Graphs: The Case of Company Ownership Graphs" (PDF). EDBT: 555--566.
- Atzeni, Paolo; Bellomarini, Luigi; Iezzi, Michela; Sallinger, Emanuel; Vlad, Adriano (2020). "Augmenting Logic-based Knowledge Graphs: The Case of Company Graphs" (PDF). Kr4L@ Ecai: 22--27.
- Baldazzi, Teodoro; Benedetto, Davide; Brandetti, Matteo; Vlad, Adriano; Bellomarini, Luigi; Sallinger, Emanuel (2022). "Datalog-based Reasoning with Heuristics over Knowledge Graphs" (PDF). International Datalog 2.0 Workshop.