Tetrahedral cupola
In 4-dimensional geometry, the tetrahedral cupola is a polychoron bounded by one tetrahedron, a parallel cuboctahedron, connected by 10 triangular prisms, and 4 triangular pyramids.[1]
| Tetrahedral cupola | ||
|---|---|---|
 Schlegel diagram | ||
| Type | Polyhedral cupola | |
| Schläfli symbol | {3,3} v rr{3,3} | |
| Cells | 16 | 1 rr{3,3} 1+4 {3,3} 4+6 {}×{3} |
| Faces | 42 | 24 triangles 18 squares |
| Edges | 42 | |
| Vertices | 16 | |
| Dual | ||
| Symmetry group | [3,3,1], order 24 | |
| Properties | convex, regular-faced | |
Related polytopes
The tetrahedral cupola can be sliced off from a runcinated 5-cell, on a hyperplane parallel to a tetrahedral cell. The cuboctahedron base passes through the center of the runcinated 5-cell, so the Tetrahedral cupola contains half of the tetrahedron and triangular prism cells of the runcinated 5-cell. The cupola can be seen in A2 and A3 Coxeter plane orthogonal projection of the runcinated 5-cell:
| A3 Coxeter plane | ||
|---|---|---|
| Runcinated 5-cell | Tetrahedron (Cupola top) |
Cuboctahedron (Cupola base) |
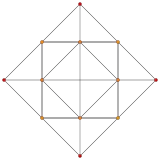 |
 |
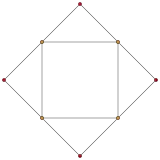 |
| A2 Coxeter plane | ||
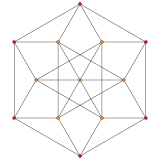 |
 |
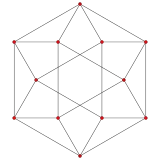 |
See also
- Tetrahedral pyramid (5-cell)
References
- Convex Segmentochora Dr. Richard Klitzing, Symmetry: Culture and Science, Vol. 11, Nos. 1-4, 139-181, 2000 (4.23 tetrahedron || cuboctahedron)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.