Soft graviton theorem

In physics, the soft graviton theorem, first formulated by Steven Weinberg in 1965,[1] allows calculation of the S-matrix, used in calculating the outcome of collisions between particles, when low-energy (soft) gravitons come into play.

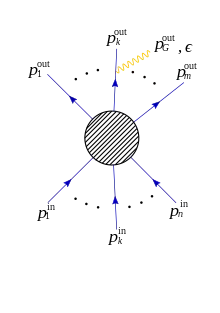
Scattering of n incoming and m outcoming particles with an outgoing graviton added to one outcoming leg.

Specifically, if in a collision between n incoming particles from which m outgoing particles arise, the outcome of the collision depends on a certain S matrix, by adding one or more gravitons to the n + m particles, the resulting S matrix (let it be S') differs from the initial S only by a factor that does not depend in any way, except for the momentum, on the type of particles to which the gravitons couple.[2]

The theorem also holds by putting photons in place of gravitons, thus obtaining a corresponding soft photon theorem.

The theorem is used in the context of attempts to formulate a theory of quantum gravity in the form of a perturbative quantum theory, that is, as an approximation of a possible, as yet unknown, exact theory of quantum gravity.[3]

In 2014 Andrew Strominger and Freddy Cachazo expanded the soft graviton theorem, gauge invariant under translation, to the subleading term of the series, obtaining the gauge invariance under rotation (implying global angular momentum conservation) and connected this to the gravitational spin memory effect.[4]

Formulation

Given particles whose interaction is described by a certain initial S matrix, by adding a soft graviton (i.e., whose energy is negligible compared to the energy of the other particles) that couples to one of the incoming or outgoing particles, the resulting S' matrix is, leaving off some kinematic factors,

${\cal {S}}'={\sqrt {8\pi G}}{\frac {\eta p^{\mu }p^{\nu }\epsilon _{\mu \nu }}{p\cdot p_{G}-i\eta \varepsilon }}{\cal {S}}+O(p_{G}^{0})$ ,[1][5]

where p is the momentum of the particle interacting with the graviton, ϵ_μν is the graviton polarization, p_G is the momentum of the graviton, ε is an infinitesimal real quantity which helps to shape the integration contour, and the factor η is equal to 1 for outgoing particles and -1 for incoming particles.

The formula comes from a power series and the last term with the big O indicates that terms of higher order are not considered. Although the series differs depending on the spin of the particle coupling to the graviton, the lowest-order term shown above is the same for all spins.[1]

In the case of multiple soft gravitons involved, the factor in front of S is the sum of the factors due to each individual graviton.

If a soft photon (whose energy is negligible compared to the energy of the other particles) is added instead of the graviton, the resulting matrix S' is

${\cal {S}}'={\frac {\eta qp\cdot \epsilon }{p\cdot p_{\gamma }-i\eta \varepsilon }}{\cal {S}}+O(p_{\gamma }^{0})$ ,[1][5]

with the same parameters as before but with p_γ momentum of the photon, ϵ is its polarization, and q the charge of the particle coupled to the photon.

As for the graviton, in case of more photons, a sum over all the terms occurs.

Subleading order expansion

The expansion of the formula to the subleading term of the series for the graviton was calculated by Andrew Strominger and Freddy Cachazo:[4]

${\cal {S}}'={\sqrt {8\pi G}}{\frac {\eta p^{\mu }p^{\nu }\epsilon _{\mu \nu }}{p\cdot p_{G}-i\eta \varepsilon }}{\cal {S}}-i{\sqrt {8\pi G}}{\frac {\eta p^{\mu }({p_{G}}_{\rho }J^{\rho \nu })\epsilon _{\mu \nu }}{p\cdot p_{G}-i\eta \varepsilon }}{\cal {S}}+O(p_{G}^{1})$ ,

where $J^{\rho \nu }$ represents the angular momentum of the particle interacting with the graviton.

This formula is gauge invariant under rotation and is connected to the gravitational spin memory effect.[4]

Notes

Weinberg, Steven (1965-10-25). "Infrared Photons and Gravitons". Physical Review. 140 (2B): B516–B524. Bibcode:1965PhRv..140..516W. doi:10.1103/PhysRev.140.B516.
He, Temple; Lysov, Vyacheslav; Mitra, Prahar; Strominger, Andrew (2015-05-07). "BMS supertranslations and Weinberg's soft graviton theorem". Journal of High Energy Physics. 2015 (5): 151. arXiv:1401.7026. Bibcode:2015JHEP...05..151H. doi:10.1007/JHEP05(2015)151. ISSN 1029-8479. S2CID 256013139.
Verma, Mritunjay. Soft Graviton Theorem in Generic Quantum Theory of Gravity (PDF). Harish-Chandra Research Institute.
Cachazo, Freddy; Strominger, Andrew (2014). "Evidence for a New Soft Graviton Theorem". arXiv:1404.4091 [hep-th].
Strominger, Andrew (2018-03-06). Lectures on the Infrared Structure of Gravity and Gauge Theory. Princeton University Press. pp. 35–36. ISBN 978-0-691-17950-6.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Weinberg, Steven (1965-10-25). "Infrared Photons and Gravitons". Physical Review. 140 (2B): B516–B524. Bibcode:1965PhRv..140..516W. doi:10.1103/PhysRev.140.B516.

[2] He, Temple; Lysov, Vyacheslav; Mitra, Prahar; Strominger, Andrew (2015-05-07). "BMS supertranslations and Weinberg's soft graviton theorem". Journal of High Energy Physics. 2015 (5): 151. arXiv:1401.7026. Bibcode:2015JHEP...05..151H. doi:10.1007/JHEP05(2015)151. ISSN 1029-8479. S2CID 256013139.

[3] Verma, Mritunjay. Soft Graviton Theorem in Generic Quantum Theory of Gravity (PDF). Harish-Chandra Research Institute.

[:2-4] Cachazo, Freddy; Strominger, Andrew (2014). "Evidence for a New Soft Graviton Theorem". arXiv:1404.4091 [hep-th].

[:1-5] Strominger, Andrew (2018-03-06). Lectures on the Infrared Structure of Gravity and Gauge Theory. Princeton University Press. pp. 35–36. ISBN 978-0-691-17950-6.