Schroeder stairs

Schroeder stairs (Schröder's stairs) is an optical illusion which is a two-dimensional drawing which may be perceived either as a drawing of a staircase leading from left to right downwards or the same staircase only turned upside down, a classical example of perspective reversal in psychology of perception. It is named after the German natural scientist Heinrich G. F. Schröder, who published it in 1858.[1][2]

Schroeder stairs can be perceived in two ways, depending on whether the viewer considers A or B to be the closer wall.

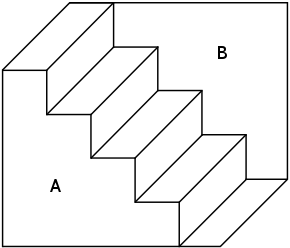
It is sometimes called "Schouten steps",[3] in reference to a small sheet-metal staircase given to M. C. Escher by Prof. Schouten and which was an inspiration for Escher's Convex and Concave.[4] This illusion is also seen in another Escher's work, Relativity.[3]

This drawing may be variously described as an "ambiguous figure", "reversible figure" or "bistable figure". The first classification refers to the likelihood that the drawing may be perceived as two (or more) different objects. The second refers to the phenomenon that after some time of staring at the figure the perception of its orientation becomes involuntarily reversed.[2] The third one emphasizes the fact that there are two (rather than one) stable perceptions of the drawing.[5]

This illusion, among others, has been used in studies of perception. In particular, in one study it was established that involuntary switch of perception occurs with approximate frequency of once in 7.5-12.5 seconds.[6] The change of perception may be attributed either to neuronal fatigue or to conscious selection.[7]