Rotating wall technique

Single-component plasmas (SCP), which are a type of nonneutral plasma, have many uses, including studying a variety of plasma physics phenomena [1] and for the accumulation, storage and delivery of antiparticles. Applications include the creation and study of antihydrogen,[2][3][4] beams to study the interaction of positrons with ordinary matter and to create dense gases of positronium (Ps) atoms,[5][6][7] and the creation of Ps-atom beams.[8][9] The “rotating wall (RW) technique” uses rotating electric fields to compress SCP in PM traps radially to increase the plasma density and/or to counteract the tendency of plasma to diffuse radially out of the trap. It has proven crucial in improving the quality and hence utility of trapped plasmas and trap-based beams.

For this application, a plasma is stored in a Penning–Malmberg (PM) trap[1] in a uniform magnetic field, B. The charge cloud is typically cylindrical in shape with dimension along B large compared to the radius. This charge produces a radial electric field which would tend to push the plasma outward. To counteract this, the plasma spins about the axis of symmetry producing a Lorentz force to balance that due to the electric field, and the plasma takes the form of a spinning charged rod. Such cold, single-component plasmas in PM traps can come to thermal equilibrium and rotate as a rigid body at frequency

${\displaystyle f_{E}={\frac {\mathrm {e} n}{\mathrm {4\pi \varepsilon _{0}} B}}}$,

where n is the plasma density.[10] As illustrated in Fig. 1, the RW technique uses an azimuthally segmented cylindrical electrode covering a portion of a plasma. Phased, sinusoidal voltages at frequency f_RW are applied to the segments. The result is a rotating electric field perpendicular to the axis of symmetry of the plasma. This field induces an electric dipole moment in the plasma and hence a torque. Rotation of the field in the direction of, and faster than the natural rotation of the plasma acts to spin the plasma faster, thereby increasing the Lorentz force and producing plasma compression (cf. Figs. 2 and 3).[11]

Fig. 1. Apparatus used to radially compress electron plasmas in a Penning–Malmberg trap using the RW technique by applying phased sinusoidal electrical signals to a segmented (RW) electrode.

Fig. 2. Radial compression of an electron plasma vs time with the RW fields turned on at t = 0. Note the log scale for density and the flat density profiles, before and after compression, that are characteristic of rigid plasma rotation.

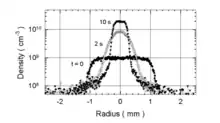
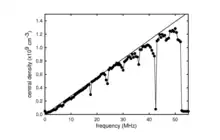
An important requirement for plasma compression using the RW technique is good coupling between the plasma and the rotating field. This is necessary to overcome asymmetry-induced transport which acts as a drag on the plasma and tends to oppose the RW torque. For high quality PM traps with little asymmetry induced transport, one can access a so-called “strong drive regime."[11][12] In this case, application of a rotating electric field at frequency results in the plasma spinning up to the applied frequency, namely f_E = f_RW (cf. Fig. 3). This has proven enormously useful as a way to fix plasma density simply by adjusting f_RW.

Fig. 3. Density of a positron plasma as a function of applied RW frequency. The solid line corresponds to f_E = f_RW, characteristic of the strong drive regime. For this experiment, B = 0.04 T, and the maximum density achieved is 17% of the Brillouin density limit,[5] which is the maximum possible density for a SCP confined in a field of strength B.

The RW technique was first developed by Huang et al., to compress a magnetized Mg⁺ plasma.[13] The technique was soon thereafter applied to electron plasmas, where a segmented electrode, such as that described above, was used to couple to waves (Trivelpiece-Gould modes) in the plasma.[14] The technique was also used to phase-lock the rotation frequency of laser cooled single-component ion crystals.[15] The first use of the RW technique for antimatter was done using small positron plasmas without coupling to modes.[16] The strong drive regime, which was discovered somewhat later using electron plasmas,[17] has proven to be more useful in that tuning to (and tracking) plasma modes is unnecessary. A related technique has been developed to compress single-component charged gases in PM traps (i.e., charge clouds not in the plasma regime).[18][19]

The RW technique has found extensive use in manipulating antiparticles in Penning–Malmberg traps. One important application is the creation of specially tailored antiparticle beams for atomic physics experiments.[5] Frequently one would like a beam with a large current density. In this case, one compresses the plasma with the RW technique before delivery. This has been crucial in experiments to study dense gases of positronium (Ps) atoms and formation of the Ps₂ molecule (e⁺e⁻e⁺e⁻) [5-7]. It has also been important in the creation of high-quality Ps-atom beams.[8][9]

The RW technique is used in three ways in the creation of low-energy antihydrogen atoms. Antiprotons are compressed radially by sympathetic compression with electrons co-loaded in the trap. The technique has also been used to fix the positron density before the positrons and antiprotons are combined.[2][3] Recently it was discovered that one could set all of the important parameters of the electron and positron plasmas for antihydrogen production using the RW to fix the plasma density and evaporative cooling to cool the plasma and fix the on-axis space charge potential. The result was greatly increased reproducibility for antihydrogen production.[4] In particular, this technique, dubbed SDREVC (strong drive regime evaporative cooling),[20] was successful to the extent that it increased the number of trappable antihydrogen by an order of magnitude. This is particularly important in that, while copious amounts of antihydrogen can be produced, the vast majority are at high temperature and cannot be trapped in the small well depth of the minimum-magnetic field atom traps.[21]

• Positron
• Antiproton
• Penning trap
• Non-neutral plasmas
• Annihilation
• Positronium
• Antihydrogen