Rectangular mask short-time Fourier transform
In mathematics and Fourier analysis, a rectangular mask short-time Fourier transform (rec-STFT) has the simple form of short-time Fourier transform. Other types of the STFT may require more computation time than the rec-STFT.
The rectangular mask function can be defined for some bound (B) over time (t) as
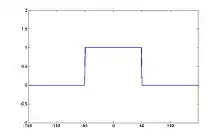
B = 50, x-axis (sec)
We can change B for different tradeoffs between desired time resolution and frequency resolution.
Rec-STFT
Inverse form
Property
Rec-STFT has similar properties with Fourier transform
- Integration
(a)
(b)
- Shifting property (shift along x-axis)
- Modulation property (shift along y-axis)
- special input
- When
- When
- Linearity property
If ,and are their rec-STFTs, then
- Power integration property
- Energy sum property (Parseval's theorem)
Example of tradeoff with different B
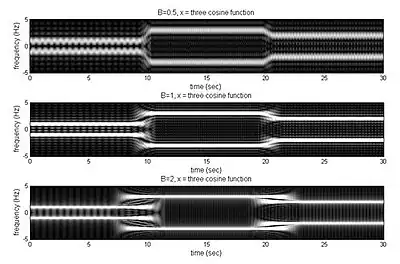
Spectrograms produced from applying a rec-STFT on a function consisting of 3 consecutive cosine waves. (top spectrogram uses smaller B of 0.5, middle uses B of 1, and bottom uses larger B of 2.)
From the image, when B is smaller, the time resolution is better. Otherwise, when B is larger, the frequency resolution is better.
Advantage and disadvantage
Compared with the Fourier transform:
- Advantage: The instantaneous frequency can be observed.
- Disadvantage: Higher complexity of computation.
Compared with other types of time-frequency analysis:
- Advantage: Least computation time for digital implementation.
- Disadvantage: Quality is worse than other types of time-frequency analysis. The jump discontinuity of the edges of the rectangular mask results in Gibbs ringing artifacts in the frequency domain, which can be alleviated with smoother windows.
See also
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.