Pseudosphere

Tractroid

The same surface can be also described as the result of revolving a tractrix about its asymptote. For this reason the pseudosphere is also called tractroid. As an example, the (half) pseudosphere (with radius 1) is the surface of revolution of the tractrix parametrized by[2]

${\displaystyle t\mapsto \left(t-\tanh {t},\operatorname {sech} \,{t}\right),\quad \quad 0\leq t<\infty .}$

It is a singular space (the equator is a singularity), but away from the singularities, it has constant negative Gaussian curvature and therefore is locally isometric to a hyperbolic plane.

The name "pseudosphere" comes about because it has a two-dimensional surface of constant negative Gaussian curvature, just as a sphere has a surface with constant positive Gaussian curvature. Just as the sphere has at every point a positively curved geometry of a dome the whole pseudosphere has at every point the negatively curved geometry of a saddle.

As early as 1693 Christiaan Huygens found that the volume and the surface area of the pseudosphere are finite,[3] despite the infinite extent of the shape along the axis of rotation. For a given edge radius R, the area is 4πR² just as it is for the sphere, while the volume is 2/3πR³ and therefore half that of a sphere of that radius.[4][5]

The pseudosphere and its relation to three other models of hyperbolic geometry

The half pseudosphere of curvature −1 is covered by the interior of a horocycle. In the Poincaré half-plane model one convenient choice is the portion of the half-plane with y ≥ 1.[6] Then the covering map is periodic in the x direction of period 2π, and takes the horocycles y = c to the meridians of the pseudosphere and the vertical geodesics x = c to the tractrices that generate the pseudosphere. This mapping is a local isometry, and thus exhibits the portion y ≥ 1 of the upper half-plane as the universal covering space of the pseudosphere. The precise mapping is

${\displaystyle (x,y)\mapsto {\big (}v(\operatorname {arcosh} y)\cos x,v(\operatorname {arcosh} y)\sin x,u(\operatorname {arcosh} y){\big )}}$

where

${\displaystyle t\mapsto {\big (}u(t)=t-\operatorname {tanh} t,v(t)=\operatorname {sech} t{\big )}}$

is the parametrization of the tractrix above.

Deforming the pseudosphere to a portion of Dini's surface. In differential geometry, this is a Lie transformation. In the corresponding solutions to the Sine-Gordon equation, this deformation corresponds to a Lorentz Boost of the static 1-soliton solution.

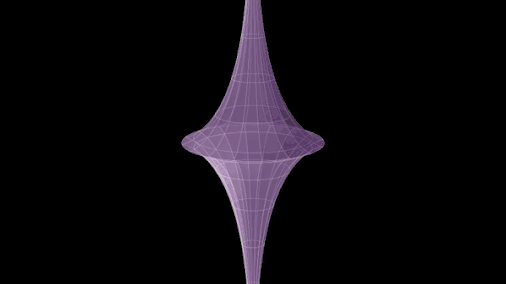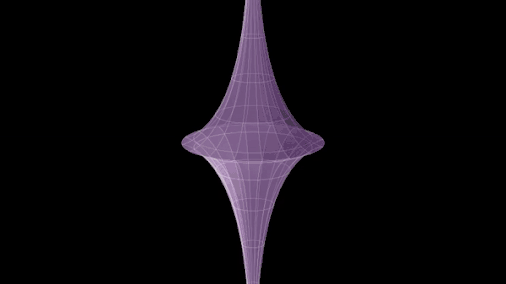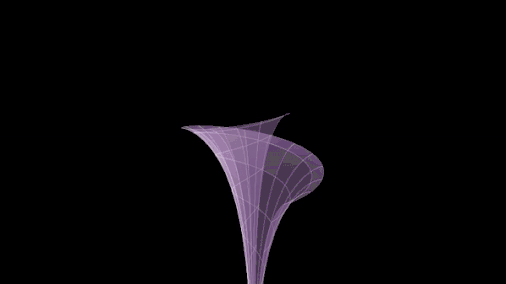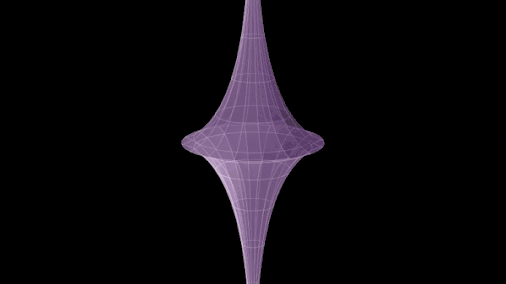
In some sources that use the hyperboloid model of the hyperbolic plane, the hyperboloid is referred to as a pseudosphere.[7] This usage of the word is because the hyperboloid can be thought of as a sphere of imaginary radius, embedded in a Minkowski space.

A pseudospherical surface is a generalization of the pseudosphere. A surface which is piecewise smoothly immersed in ${\displaystyle \mathbb {R} ^{3}}$ with constant negative curvature is a pseudospherical surface. The tractroid is the simplest example. Other examples include the Dini's surfaces, breather surfaces, and the Kuen surface.

Pseudospherical surfaces can be constructed from solutions to the Sine-Gordon equation.[8] A sketch proof starts with reparametrizing the tractroid with coordinates in which the Gauss–Codazzi equations can be rewritten as the Sine-Gordon equation.

In particular, for the tractroid the Gauss–Codazzi equations are the Sine-Gordon equation applied to the static soliton solution, so the Gauss–Codazzi equations are satisfied. In these coordinates the first and second fundamental forms are written in a way that makes clear the Gaussian curvature is -1 for any solution of the Sine-Gordon equations.

Then any solution to the Sine-Gordon equation can be used to specify a first and second fundamental form which satisfy the Gauss–Codazzi equations. There is then a theorem that any such set of initial data can be used to at least locally specify an immersed surface in ${\displaystyle \mathbb {R} ^{3}}$.

A few examples of Sine-Gordon solutions and their corresponding surface are given as follows:

• Static 1-soliton: pseudosphere
• Moving 1-soliton: Dini's surface
• Breather solution: Breather surface
• 2-soliton: Kuen surface

• Hilbert's theorem (differential geometry)
• Dini's surface
• Gabriel's Horn
• Hyperboloid
• Hyperboloid structure
• Quasi-sphere
• Sine–Gordon equation
• Sphere
• Surface of revolution

• Stillwell, J. (1996). Sources of Hyperbolic Geometry. Amer. Math. Soc & London Math. Soc.
• Henderson, D. W.; Taimina, D. (2006). "Experiencing Geometry: Euclidean and Non-Euclidean with History". Aesthetics and Mathematics (PDF). Springer-Verlag.
• Kasner, Edward; Newman, James (1940). Mathematics and the Imagination. Simon & Schuster. pp. 140, 145, 155.

• Non Euclid
• Crocheting the Hyperbolic Plane: An Interview with David Henderson and Daina Taimina
• Norman Wildberger lecture 16, History of Mathematics, University of New South Wales. YouTube. 2012 May.
• Pseudospherical surfaces at the virtual math museum.