Predictive coding

Theoretical ancestors to predictive coding date back as early as 1860 with Helmholtz's concept of unconscious inference.[4] Unconscious inference refers to the idea that the human brain fills in visual information to make sense of a scene. For example, if something is relatively smaller than another object in the visual field, the brain uses that information as a likely cue of depth, such that the perceiver ultimately (and involuntarily) experiences depth. The understanding of perception as the interaction between sensory stimuli (bottom-up) and conceptual knowledge (top-down) continued to be established by Jerome Bruner who, starting in the 1940s, studied the ways in which needs, motivations and expectations influence perception, research that came to be known as 'New Look' psychology. In 1981, McClelland and Rumelhart in their seminal paper[5] examined the interaction between processing features (lines and contours) which form letters, which in turn form words. While the features suggest the presence of a word, they found that when letters were situated in the context of a word, people were able to identify them faster than when they were situated in a non-word without semantic context. McClelland and Rumelhart's parallel processing model describes perception as the meeting of top-down (conceptual) and bottom-up (sensory) elements.

In the late 1990s, the idea of top-down and bottom-up processing was translated into a computational model of vision by Rao and Ballard.[6] Their paper demonstrated that there could be a generative model of a scene (top-down processing), which would receive feedback via error signals (how much the visual input varied from the prediction), which would subsequently lead to updating the prediction. The computational model was able to replicate well-established receptive field effects, as well as less understood extra-classical receptive field effects such as end-stopping.

In 2004,[7] Rick Grush proposed a model of neural perceptual processing according to which the brain constantly generates predictions based on a generative model (what Grush called an ‘emulator’), and compares that prediction to the actual sensory input. The difference, or ‘sensory residual’ would then be used to update the model so as to produce a more accurate estimate of the perceived domain. On Grush’s account, the top-down and bottom up signals would be combined in a way sensitive to the expected noise (aka uncertainty) in the bottom-up signal, so that in situations in which the sensory signal was known to be less trustworthy, the top-down prediction would be given greater weight, and vice-versa. The emulation framework was also shown to be hierarchical, with modality-specific emulators providing top-down expectations for sensory signals as well as higher-level emulators providing expectations of the distal causes of those signals. Grush applied the theory to visual perception, visual and motor imagery, language, and theory of mind phenomena.

Today, the fields of computer science and cognitive science incorporate these same concepts to create the multilayer generative models that underlie machine learning and neural nets.[8]

Conceptual Schematic of Predictive Coding with 2 levels

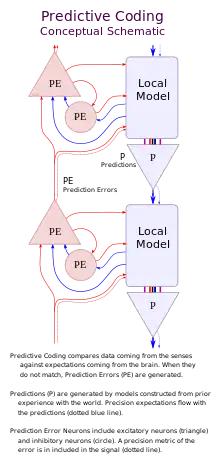
Most of the research literature in the field has been about sensory perception, particularly vision, which is more easily conceptualized. However, the predictive coding framework could also be applied to different neural systems. Taking the sensory system as an example, the brain solves the seemingly intractable problem of modelling distal causes of sensory input through a version of Bayesian inference. It does this by modelling predictions of lower-level sensory inputs via backward connections from relatively higher levels in a cortical hierarchy.[9] Constrained by the statistical regularities of the outside world (and certain evolutionarily prepared predictions), the brain encodes top-down generative models at various temporal and spatial scales in order to predict and effectively suppress sensory inputs rising up from lower levels. A comparison between predictions (priors) and sensory input (likelihood) yields a difference measure (e.g. prediction error, free energy, or surprise) which, if it is sufficiently large beyond the levels of expected statistical noise, will cause the generative model to update so that it better predicts sensory input in the future.

In general, it can be more easily stated that it minimizes the amount of surprise (the measure of difference). This is also the reason for what is nowadays called confirmation bias or what might historically be prejudice (although the latter has more negative connotations) since it better fits one's individual experience accumulated so far and supports consistency. Therefore, this turns out to be rather a disadvantage in today's world.[10]

If, instead, the model accurately predicts driving sensory signals, activity at higher levels cancels out activity at lower levels, and the posterior probability of the model is increased. Thus, predictive coding inverts the conventional view of perception as a mostly bottom-up process, suggesting that it is largely constrained by prior predictions, where signals from the external world only shape perception to the extent that they are propagated up the cortical hierarchy in the form of prediction error.

In predictive coding, errors are neither good nor bad, but simply signal the difference between the expected and actual input. The exception is in reward processing, where a better than expected reward produces a positive prediction error and a disappointing result produces a negative prediction error.[11]

Evaluating the empirical evidence that suggests a neurologically plausible basis for predictive coding is a broad and varied task. For one thing, and according to the model, predictive coding occurs at every iterative step in the perceptual and cognitive processes; accordingly, manifestations of predictive coding in the brain include genetics, specific cytoarchitecture of cells, systemic networks of neurons, and whole brain analyses. Due to this range of specificity, different methods of investigating the neural mechanisms of predictive coding have been applied, where available; more generally, however, and at least as it relates to humans, there are significant methodological limitations to investigating the potential evidence and much of the work is based on computational modeling of microcircuits in the brain. Notwithstanding, there has been substantial (theoretical) work that has been applied to understanding predictive coding mechanisms in the brain. This section will focus on specific evidence as it relates to the predictive coding phenomenon, rather than analogues, such as homeostasis (which are, nonetheless, integral to our overall understanding of Bayesian inference but already supported heavily; see Clark for a review[9]).

Much of the early work that applied a predictive coding framework to neural mechanisms came from sensory neurons, particularly in the visual cortex.[6][16]

More generally, however, what seems to be required by the theory are (at least) two types of neurons (at every level of the perceptual hierarchy): one set of neurons that encode incoming sensory input, so called feed-forward projections; one set of neurons that send down predictions, so called feed-backward projections. It is important to note that these neurons must also carry properties of error detection; which class of neurons has these properties is still up for debate.[17][18] These sort of neurons have found support in superficial and non-superficial pyramidal neurons.

At a more whole-brain level, there is evidence that different cortical layers (aka laminae) may facilitate the integration of feedforward and feed-backward projections across hierarchies. These cortical layers, divided into granular, agranular, and dysgranular, which house the subpopulations of neurons mentioned above, are divided into 6 main layers. The cytoarchitecture within these layers are the same, but they differ across layers. For example, layer 4 of the granular cortex contain granule cells which are excitatory and distribute thalamocortical inputs to the rest of the cortex. According to one model:

“...prediction neurons... in deep layers of agranular cortex drive active inference by sending sensory predictions via projections ...to supragranular layers of dysgranular and granular sensory cortices. Prediction-error neurons ….in the supragranular layers of granular cortex compute the difference between the predicted and received sensory signal, and send prediction-error signals via projections...back to the deep layers of agranular cortical regions. Precision cells … tune the gain on predictions and prediction error dynamically, thereby giving these signals reduced (or, in some cases, greater) weight depending on the relative confidence in the descending predictions or the reliability of incoming sensory signals.”[19]

The theory that the unit of prediction is the cortical column[20] is based on the remarkable correspondence between the microcircuitry of the cortical column and the connectivity implied by predictive coding.[21]