Pariah group
In group theory, the term pariah was introduced by Robert Griess in Griess (1982) to refer to the six sporadic simple groups which are not subquotients of the monster group.
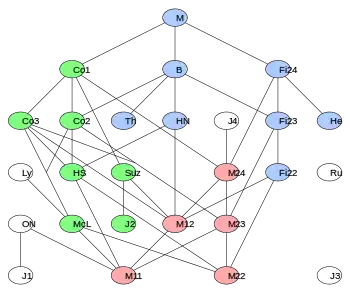
Relationships among the sporadic simple groups. The monster group M is at the top, and the groups which are descended from it are the happy family.
The six which are not connected by an upward path to M (white ellipses) are the pariahs.
The six which are not connected by an upward path to M (white ellipses) are the pariahs.
The twenty groups which are subquotients, including the monster group itself, he dubbed the happy family.
For example, the orders of J4 and the Lyons Group Ly are divisible by 37. Since 37 does not divide the order of the monster, these cannot be subquotients of it; thus J4 and Ly are pariahs. Three other sporadic groups were also shown to be pariahs by Griess in 1982, and the Janko Group J1 was shown to be the final pariah by Robert A. Wilson in 1986. The complete list is shown below.
| Group | Size | Approx. size |
Factorized order |
|---|---|---|---|
| Lyons group, Ly | 51765179004000000 | 5×1016 | 28 · 37 · 56 · 7 · 11 · 31 · 37 · 67 |
| O'Nan group, O'N | 460815505920 | 5×1011 | 29 · 34 · 5 · 73 · 11 · 19 · 31 |
| Rudvalis group, Ru | 145926144000 | 1×1011 | 214 · 33 · 53 · 7 · 13 · 29 |
| Janko group, J4 | 86775571046077562880 | 9×1019 | 221 · 33 · 5 · 7 · 113 · 23 · 29 · 31 · 37 · 43 |
| Janko group, J3 | 50232960 | 5×107 | 27 · 35 · 5 · 17 · 19 |
| Janko group, J1 | 175560 | 2×105 | 23 · 3 · 5 · 7 · 11 · 19 |
References
- Griess, Robert L. (February 1982), "The friendly giant" (PDF), Inventiones Mathematicae, 69 (1): 1–102, Bibcode:1982InMat..69....1G, doi:10.1007/BF01389186, hdl:2027.42/46608, ISSN 0020-9910, MR 0671653, S2CID 123597150
- Robert A. Wilson (1986). Is J1 a subgroup of the monster?, Bull. London Math. Soc. 18, no. 4 (1986), 349-350
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.