NAND logic

A NAND gate is an inverted AND gate. It has the following truth table:

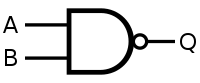Q = A NAND B Truth Table Input A Input B Output Q 0 0 1 0 1 1 1 0 1 1 1 0

A CMOS transistor NAND element. V_dd denotes positive voltage.

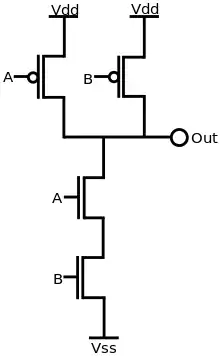
In CMOS logic, if both of the A and B inputs are high, then both the NMOS transistors (bottom half of the diagram) will conduct, neither of the PMOS transistors (top half) will conduct, and a conductive path will be established between the output and Vss (ground), bringing the output low. If both of the A and B inputs are low, then neither of the NMOS transistors will conduct, while both of the PMOS transistors will conduct, establishing a conductive path between the output and Vdd (voltage source), bringing the output high. If either of the A or B inputs is low, one of the NMOS transistors will not conduct, one of the PMOS transistors will, and a conductive path will be established between the output and Vdd (voltage source), bringing the output high. As the only configuration of the two inputs that results in a low output is when both are high, this circuit implements a NAND (NOT AND) logic gate.

A NAND gate is a universal gate, meaning that any other gate can be represented as a combination of NAND gates.

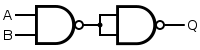
NOT

See also: NOT gate

A NOT gate is made by joining the inputs of a NAND gate together. Since a NAND gate is equivalent to an AND gate followed by a NOT gate, joining the inputs of a NAND gate leaves only the NOT gate.

Desired NOT Gate	NAND Construction
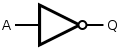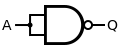Q = NOT( A )	= A NAND A
Truth Table Input A Output Q 0 1 1 0

AND

See also: AND gate

An AND gate is made by inverting the output of a NAND gate as shown below.

Desired AND Gate	NAND Construction
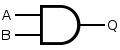Q = A AND B	= ( A NAND B ) NAND ( A NAND B )
Truth Table Input A Input B Output Q 0 0 0 0 1 0 1 0 0 1 1 1

OR

See also: OR gate

If the truth table for a NAND gate is examined or by applying De Morgan's Laws, it can be seen that if any of the inputs are 0, then the output will be 1. To be an OR gate, however, the output must be 1 if any input is 1. Therefore, if the inputs are inverted, any high input will trigger a high output.

Desired OR Gate	NAND Construction
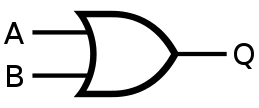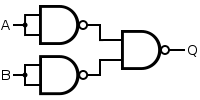Q = A OR B	= ( A NAND A ) NAND ( B NAND B )
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 1

NOR

See also: NOR gate

A NOR gate is an OR gate with an inverted output. Output is high when neither input A nor input B is high.

Desired NOR Gate	NAND Construction
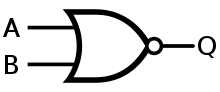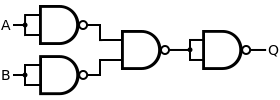Q = A NOR B	= [ ( A NAND A ) NAND ( B NAND B ) ] NAND [ ( A NAND A ) NAND ( B NAND B ) ]
Truth Table Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 0

XOR

See also: XOR gate

An XOR gate is made by connecting four NAND gates as shown below. This construction entails a propagation delay three times that of a single NAND gate.

Desired XOR Gate	NAND Construction
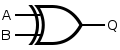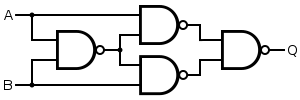Q = A XOR B	= [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ]
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 0

Alternatively, an XOR gate is made by considering the disjunctive normal form ${\displaystyle A\cdot {\overline {B}}+{\overline {A}}\cdot B}$, noting from de Morgan's Law that a NAND gate is an inverted-input OR gate. This construction uses five gates instead of four.

Desired Gate	NAND Construction
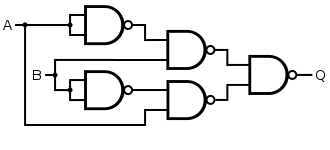Q = A XOR B	= [ B NAND ( A NAND A ) ] NAND [ A NAND ( B NAND B ) ]

XNOR

See also: XNOR gate

An XNOR gate is made by considering the disjunctive normal form ${\displaystyle A\cdot B+{\overline {A}}\cdot {\overline {B}}}$, noting from de Morgan's Law that a NAND gate is an inverted-input OR gate. This construction entails a propagation delay three times that of a single NAND gate and uses five gates.

Desired XNOR Gate	NAND Construction
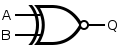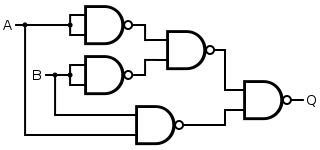Q = A XNOR B	= [ ( A NAND A ) NAND ( B NAND B ) ] NAND ( A NAND B )
Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 1

Alternatively, the 4-gate version of the XOR gate can be used with an inverter. This construction has a propagation delay four times (instead of three times) that of a single NAND gate.

Desired Gate	NAND Construction
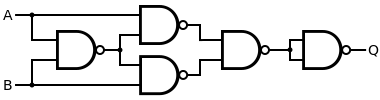Q = A XNOR B	= { [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ] } NAND { [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ] }

A multiplexer or a MUX gate is a three-input gate that uses one of the inputs, called the selector bit, to select one of the other two inputs, called data bits, and outputs only the selected data bit.[1]

A demultiplexer performs the opposite function of a multiplexer: It takes a single input and channels it to one of two possible outputs according to a selector bit that specifies which output to choose.[1]

• CMOS transistor structures and chip deposition geometries that produce NAND logic elements
• Sheffer stroke – other name
• NOR logic. Like NAND gates, NOR gates are also universal gates.
• Functional completeness

• TTL NAND and AND gates - All About Circuits
• Steps to Derive XOR from NAND gate.
• NandGame - a game about building a computer using only NAND gates

• Lancaster, Don (1974). TTL Cookbook (1st ed.). Indianapolis, IN: Howard W Sams. pp. 126–135. ISBN 0-672-21035-5.
• Sheffer, H. M. (1913), "A set of five independent postulates for Boolean algebras, with application to logical constants", Transactions of the American Mathematical Society, 14: 481–488, doi:10.2307/1988701, JSTOR 1988701