Majority judgment
Majority judgment (MJ) is a single-winner voting system proposed in 2010 by Michel Balinski and Rida Laraki.[1][2][3] It uses a highest median rule, i.e., a cardinal voting system that elects the candidate with the highest median rating.
| Part of the Politics series |
| Electoral systems |
|---|
.svg.png.webp) |
|
|
Unlike other voting methods, MJ guarantees that the winner between three or more candidates will be the candidate who had received an absolute majority of the highest grades given by all the voters.
Voting process
Voters grade as many of the candidates' as they wish with regard to their suitability for office as either Excellent (ideal), Very Good, Good, Acceptable, Poor, or Reject. Multiple candidates may be given the same grade by a voter. Any candidate not explicitly graded by a voter is counted as having been rejected by the voter. Therefore, each candidate receives the same total number of grades, but a different distribution of them.
The candidate with the highest median grade is the winner. This median-grade can be found as follows: Place all the grades, high to low, top to bottom, in side-by-side columns, the name of each candidate at the top of each of these columns. The median-grade for each candidate is the grade located halfway down each column, i.e. in the middle if there is an odd number of voters, the lower middle if the number is even. If more than one candidate has the same highest median-grade, the MJ winner is discovered by removing (one-by-one) any grades equal in value to the shared median grade from each tied candidate's column. This is repeated until only one of the previously tied candidates is currently found to have the highest median grade.[4] Equivalently, the candidates can be ranked according to a simple mathematical formula described on the page: highest median voting rules.
Discussion
As it is a highest median rule, MJ produces more informative results than the existing alternatives. It is true that if only one of two candidates is to be elected, and the winner has only a few votes more than the near winner, MJ and all the alternative voting methods would discover the same winner. However, unlike highest median rules, none of the alternative methods inform us whether the voters saw great merit in both, saw little merit in either, or saw merit in one but not the other. The published results of an MJ election reveal how many grades of each level were given to each candidate by all voters, including the median grade of each candidate.
This same educative benefit is also offered by evaluative proportional representation (EPR), an adaption of MJ to elect all the members of a legislature at the same time.[5] With EPR, each voter can also guarantee that their vote will proportionally add to the voting power of the elected member of the legislature to whom they had given their highest grade, highest remaining grade, or proxy vote. No vote is "wasted". Each voter and each self-identifying minority or majority is represented proportionately. EPR offers voters an even smaller incentive to vote tactically than does MJ (see below). Unlike MJ, each EPR voter is assured that their vote will equally increase the voting power in the legislature of the winner they give their highest grade, highest remaining grade, or proxy vote.)
Satisfied and failed criteria
Like other highest median rules, majority judgment satisfies the majority criterion for rated ballots, the monotonicity criterion, and the later-no-help criterion. By assuming that grades are given independently of other candidates, it satisfies the independence of clones criterion and the independence of irrelevant alternatives criterion, but the latter criterion is less compatible with the majority criterion if voters instead use their grades only to express preferences between the available candidates. MJ may also pass a rated ballot-analogue of the mutual majority criterion, but this is hard to understand or seems irrelevant given that this criterion asserts that if a majority of voters prefer a set of candidates above all others, then someone in this set will win so long as the majority gives everyone in the set a perfect rating and everyone not in the set a less-than-perfect rating. This is because the median voter will be someone in the majority, and they will give everyone in the set a perfect rating, and everyone not in the set a less-than-perfect rating.
Majority judgment fails reversal symmetry, e.g. a candidate whose grades are {Acceptable, Acceptable} will still beat a candidate whose ratings are {good, poor} in both directions.
Like any deterministic voting system without a dictator, MJ allows for tactical voting in case of three or more candidates. This is a consequence of Gibbard's theorem.
Majority judgment voting fails the Condorcet criterion,[note 1] later-no-harm,[note 2] consistency,[note 3] the Condorcet loser criterion,[note 4] and the participation criterion.[note 5] It also fails the ranked or preferential majority criterion, which is incompatible with the passed criterion independence of irrelevant alternatives. However, the importance of these failures are diminished by Balinski's response to the following article.
Felsenthal and Machover
In 2008, Felsenthal and Machover's article[6] discussed MJ as presented by Balinski and his associates in 2007. However, the last part of their discussion claims that MJ is "afflicted" most seriously by the fact that it can fail the tests of "participant-consistency". For example, the "no-show objection" refers to the paradox that a candidate who is given a higher grade than is needed to win can lose as a result.
In their 2010 book, Balinski and Laraki respond by explaining (pp. 285–295) that this theoretical possibility is inherent in any method which uses "medians" rather than any "point-summing" method to aggregate all citizens' votes. They go on to describe the following unlikely special circumstances that might allow such a "failure" to occur by chance when using MJ: 1) Initially, the total number of voters must be odd. 2) By these votes alone, candidate X would win and Y would lose (e.g. because X's median grade is "Very Good" and Y's is "Good"). 3) Both of the potential additional grades to be given to X and Y must either happen to be higher or lower than each competitor's current median grade. 4) The grade immediately below the current median grade of the current winner(X) must be at least two grades lower, e.g. "Acceptable" rather than "Very Good". At the same time, the grade immediately below the current median grade of the current loser, but potential winner (Y), must be higher than the grade immediately below the current median grade of the current winner(X).
For example, if the additional grades given to X were "Excellent", and "Very Good" to Y, Y would become the winner instead. Y's new median grade would be "Good" (given the above examples). X's new median grade would be "Acceptable". Balinski accepts that such paradoxes are not possible with "point-summing" counting methods, but are possible with MJ. At the same time, he argues that these are not very important. This is illustrated by the above example. The additional voter should not be very disappointed if, very rarely if ever, their "Very Good" candidate wins instead of their "Excellent" candidate. Consequently, such paradoxes are a very small price to pay for the clear advantages offered by MJ. Unlike MJ, they do not guarantee that the winner is supported by an absolute majority of all the voters, do not reveal all the grades given to all the candidates by all the voters, and do not remove, almost by "half", the opportunities and incentives to vote insincerely (tactical or strategically), and do not prompt voters as clearly—firstly to consider the qualities required by the office being sought.
Claimed resistance to tactical voting
In arguing for majority judgment, Balinski and Laraki (the system's inventors) logically and mathematically prove that highest median rule are the most "strategy-resistant" of any system that satisfies certain criteria considered desirable by the authors. They show that MJ provides only about "half" the opportunities and incentives to vote tactically (dishonestly, strategically) when compared with the alternative methods.[7]
Outcome in political environments
In 2010, J.-F. Laslier showed[8] that in "left-right" environments, majority judgment tends to favor the most homogeneous camp, instead of picking the middle-of-the-road, Condorcet winner candidate. The reason is that, by definition, finding the highest median is something like finding the best Rawlsian compromise (maximin criterion) when one allows disregarding almost half of the population.[9]
Here is a numerical example. Suppose there were seven ratings named "Excellent", "Very good", "Good", "Passable", "Inadequate", "Mediocre" and "Bad". Supposed voters belong to seven groups: Extreme Left, Left, Center Left, Center, Center Right, Right and Extreme Right, and the size of the groups are respectively: 101 voters for each of the three groups on the left, 99 for each of the three groups on the right and 50 for the centrist group. Suppose there are seven candidates, one from each group, and voters assigned their ratings to the seven candidates by giving the candidate closest to their own ideological position the rating "Excellent", and then decreasing the rating as candidates are politically further away from them:
Candidate | 101 voters Extreme left | 101 voters Left | 101 voters Center left | 50 voters Center | 99 voters Center right | 99 voters Right | 99 voters Extreme right | Median |
|---|---|---|---|---|---|---|---|---|
| Ext left | excellent | very good | good | passable | inadequate | mediocre | bad | passable |
| Left | very good | excellent | very good | good | passable | inadequate | mediocre | good |
| Center left | good | very good | excellent | very good | good | passable | inadequate | good |
| Center | passable | good | very good | excellent | very good | good | passable | good |
| Center right | inadequate | passable | good | very good | excellent | very good | good | good |
| Right | mediocre | inadequate | passable | good | very good | excellent | very good | good |
| Ext right | bad | mediocre | inadequate | passable | good | very good | excellent | passable |
The tie-breaking procedure of majority judgment elects the Left candidate, as this candidate is the one with the non-median rating closest to the median, and this non-median rating is above the median rating. In so doing, the majority judgment elects the best compromise for voters on the left side of the political axis (as they are slightly more numerous than those on the right) instead of choosing a more consensual candidate such as the center-left or the center. The reason is that the tie-breaking is based on the rating closest to the median, regardless of the other ratings.
Note that other highest median rules that take into account the ratings on either side of the median, such as the typical judgment or the usual judgment, would not elect the Left candidate as in the case of the majority judgment, but would elect the Center candidate. These other rules would in this case respect the Condorcet criterion. These methods, introduced more recently, thus verify the desirable properties of the majority judgment while avoiding its main pitfalls.[10]
| Candidate |
| |||||||||||||
| Left |
| |||||||||||||
| Center left |
| |||||||||||||
| Center |
| |||||||||||||
| Center right |
| |||||||||||||
| Right |
| |||||||||||||
|
Example application
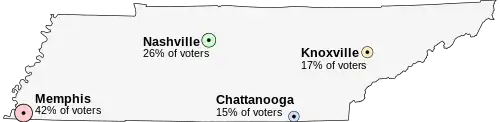
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.
The candidates for the capital are:
- Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
- Nashville, with 26% of the voters, near the center of the state
- Knoxville, with 17% of the voters
- Chattanooga, with 15% of the voters
The preferences of the voters would be divided like this:
| 42% of voters (close to Memphis) |
26% of voters (close to Nashville) |
15% of voters (close to Chattanooga) |
17% of voters (close to Knoxville) |
|---|---|---|---|
|
|
|
|
Suppose there were four ratings named "Excellent", "Good", "Fair", and "Poor", and voters assigned their ratings to the four cities by giving their own city the rating "Excellent", the farthest city the rating "Poor" and the other cities "Good", "Fair", or "Poor" depending on whether they are less than a hundred, less than two hundred, or over two hundred miles away:
City Choice | Memphis voters | Nashville voters | Chattanooga voters | Knoxville voters | Median rating[note 6] |
|---|---|---|---|---|---|
| Memphis | excellent | poor | poor | poor | poor+ |
| Nashville | fair | excellent | fair | fair | fair+ |
| Chattanooga | poor | fair | excellent | good | fair- |
| Knoxville | poor | fair | good | excellent | fair- |
Then the sorted scores would be as follows:
| City |
| |||||||||
| Nashville |
| |||||||||
| Knoxville |
| |||||||||
| Chattanooga |
| |||||||||
| Memphis |
| |||||||||
|
The median ratings for Nashville, Chattanooga, and Knoxville are all "Fair"; and for Memphis, "Poor". Since there is a tie between Nashville, Chattanooga, and Knoxville, "Fair" ratings are removed from all three, until their medians become different. After removing 16% "Fair" ratings from the votes of each, the sorted ratings are now:
| City |
| ||||||
| Nashville |
| ||||||
| Knoxville |
| ||||||
| Chattanooga |
|
Chattanooga and Knoxville now have the same number of "Poor" ratings as "Fair", "Good" and "Excellent" combined. As a result of subtracting one "Fair" from each of the tied cities, one-by-one until only one of these cities has the highest median-grade, the new and deciding median-grades of these originally tied cities are as follows: "Poor" for both Chattanooga and Knoxville, while Nashville's median remains at "Fair". So Nashville, the capital in real life, wins.
If voters were more strategic, those from Knoxville and Chattanooga might rate Nashville as "Poor" and Chattanooga as "Excellent", in an attempt to make their preferred candidate Chattanooga win. Also, Nashville voters might rate Knoxville as "poor" to distinguish it from Chattanooga. In spite of these attempts at strategy, the winner would still be Nashville. .
History
Voting theory has tended to focus more on ranked systems, so this still distinguishes MJ from most voting system proposals. Second, it uses words, not numbers, to assign a commonly understood meaning to each rating. Balinski and Laraki insist on the importance of the fact that ratings have a commonly understood absolute meaning. Firstly, MJ prompts voters to clarify in their own minds what qualities the office requires. These qualities are "absolute" in the sense that they are independent from any of the qualities any candidates might have or might not have in a future election. They are not purely relative or strategic. Again, this aspect is unusual but not unheard-of throughout the history of voting. Finally, it uses the median to aggregate ratings. This method was explicitly proposed to assign budgets by Francis Galton in 1907[11] and was implicitly used in Bucklin voting, a ranked or mixed ranked/rated system used soon thereafter in Progressive era reforms in the United States. Also, hybrid mean/median systems, which throw away a certain predefined number of outliers on each side and then average the remaining scores, have long been used to judge contests such as Olympic figure skating; such systems, like majority judgment, are intended to limit the impact of biased or strategic judges.
The full system of majority judgment was first proposed by Balinski and Laraki in 2007.[1] That same year, they used it in an exit poll of French voters in the presidential election. Although this regional poll was not intended to be representative of the national result, it agreed with other local or national experiments in showing that François Bayrou, rather than the eventual runoff winner, Nicolas Sarkozy, or two other candidates (Ségolène Royal or Jean-Marie Le Pen) would have won under most alternative rules, including majority judgment. They also note:
Everyone with some knowledge of French politics who was shown the results with the names of Sarkozy, Royal, Bayrou and Le Pen hidden invariably identified them: the grades contain meaningful information.[12]
It has since been used in judging wine competitions and in other political research polling in France and in the US.[13]
See also
Notes
- Strategically in the strong Nash equilibrium, MJ passes the Condorcet criterion.
- MJ provides a weaker guarantee similar to LNH: rating another candidate at or below your preferred winner's median rating (as opposed to one's own rating for the winner) cannot harm the winner.
- Majority judgment's inventors argue that meaning should be assigned to the absolute rating that the system assigns to a candidate; that if one electorate rates candidate X as "excellent" and Y as "good", while another one ranks X as "acceptable" and Y as "poor", these two electorates do not in fact agree. Therefore, they define a criterion they call "rating consistency", which majority judgment passes. Balinski and Laraki, "Judge, don't Vote", November 2010
- Nevertheless, it passes a slightly weakened version, the majority condorcet loser criterion, in which all defeats are by an absolute majority (if there are not equal rankings).
- It can fail the participation criterion only when, among other conditions, the new ballot rates both of the candidates in question on the same side of the winning median, and the prior distribution of ratings is more sharply peaked or irregular for one of the candidates.
- A "+" or "-" is added depending on whether the median would rise or fall if median ratings were removed, as in the tiebreaking procedure.
References
- Balinski M. and R. Laraki (2007) «A theory of measuring, electing and ranking». Proceedings of the National Academy of Sciences USA, vol. 104, no. 21, 8720-8725.
- M. Balinski & R. Laraki (2010). Majority Judgment. MIT. ISBN 978-0-262-01513-4.
- de Swart, Harrie (2021-11-16). "How to Choose a President, Mayor, Chair: Balinski and Laraki Unpacked". The Mathematical Intelligencer. 44 (2): 99–107. doi:10.1007/s00283-021-10124-3. ISSN 0343-6993. S2CID 244289281.
- Balinski and Laraki, Majority Judgment, pp.5 & 14
- Bosworth, S. et al., 2020. Electing Legislatures by Evaluative Proportional Representation (EPR): An Algorithm. https://www.jpolrisk.com/legislatures-elected-by-evaluative-proportional-representation-epr-an-algorithm-v3/ . 14 February 2023.
- Felsenthal, Dan S. and Machover, Moshé, "The Majority Judgement voting procedure: a critical evaluation", Homo oeconomicus, vol 25(3/4), pp. 319-334 (2008)
- Balinski and Laraki, Majority Judgment, pp. 15,17,19,187-198, and 374
- Jean-François Laslier (2010). "On choosing the alternative with the best median evaluation". Public Choice.
- Jean-François Laslier (2018). "The strange "Majority Judgment"". Hal.
- Fabre, Adrien (2020). "Tie-breaking the Highest Median: Alternatives to the Majority Judgment" (PDF). Social Choice and Welfare. 56: 101–124. doi:10.1007/s00355-020-01269-9. S2CID 253851085.
- Francis Galton, "One vote, one value," Letter to the editor, Nature vol. 75, Feb. 28, 1907, p. 414.
- Balinski M. and R. Laraki (2007) «Election by Majority Judgment: Experimental Evidence». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2007-28. Chapter in the book: «In Situ and Laboratory Experiments on Electoral Law Reform: French Presidential Elections», Edited by Bernard Dolez, Bernard Grofman and Annie Laurent. Springer, to appear in 2011.
- Balinski M. and R. Laraki (2010) «Judge: Don't vote». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2010-27.
Further reading
- Balinski, Michel, and Laraki, Rida (2010). Majority Judgment: Measuring, Ranking, and Electing, MIT Press