History of longitude
The history of longitude describes the centuries-long effort by astronomers, cartographers and navigators to discover a means of determining the longitude of any given place on Earth. The measurement of longitude is important to both cartography and navigation. In particular, for safe ocean navigation, knowledge of both latitude and longitude is required, however latitude can be determined with good accuracy with local astronomical observations.

Finding an accurate and practical method of determining longitude took centuries of study and invention by some of the greatest scientists and engineers. Determining longitude relative to the meridian through some fixed location requires that observations be tied to a time scale that is the same at both locations, so the longitude problem reduces to finding a way to coordinate clocks at distant places. Early approaches used astronomical events that could be predicted with great accuracy, such as eclipses, and building clocks, known as chronometers, that could keep time with sufficient accuracy while being transported great distances by ship. Later methods used the telegraph and then radio to synchronize clocks. Today the problem of longitude has been solved to centimeter accuracy through satellite navigation.
Longitude before the telescope
Eratosthenes in the 3rd century BCE first proposed a system of latitude and longitude for a map of the world. His prime meridian (line of longitude) passed through Alexandria and Rhodes, while his parallels (lines of latitude) were not regularly spaced, but passed through known locations, often at the expense of being straight lines.[1] By the 2nd century BCE Hipparchus was using a systematic coordinate system, based on dividing the circle into 360°, to uniquely specify places on Earth.[2]: 31 So longitudes could be expressed as degrees east or west of the primary meridian, as we do today (though the primary meridian is different). He also proposed a method of determining longitude by comparing the local time of a lunar eclipse at two different places, to obtain the difference in longitude between them.[2]: 11 This method was not very accurate, given the limitations of the available clocks, and it was seldom done – possibly only once, using the Arbela eclipse of 330 BCE.[3] But the method is sound, and this is the first recognition that longitude can be determined by accurate knowledge of time.
Ptolemy, in the 2nd century CE, based his mapping system on estimated distances and directions reported by travellers. Until then, all maps had used a rectangular grid with latitude and longitude as straight lines intersecting at right angles.[4]: 543 [5]: 90 For large area this leads to unacceptable distortion, and for his map of the inhabited world, Ptolemy used projections (to use the modern term) with curved parallels that reduced the distortion. No maps (or manuscripts of his work) exist that are older than the 13th century, but in his Geography he gave detailed instructions and latitude and longitude coordinates for hundreds of locations that are sufficient to re-create the maps. While Ptolemy's system is well-founded, the actual data used are of very variable quality, leading to many inaccuracies and distortions.[6][4]: 551–553 [7] Apart from the difficulties in estimating rectilinear distances and directions, the most important of these is a systematic over-estimation of differences in longitude. Thus from Ptolemy's tables, the difference in Longitude between Gibraltar and Sidon is 59° 40' 0', compared to the modern value of 40° 23'0', about 48% too high. Russo (2013) has analysed these discrepancies, and concludes that much of the error arises from Ptolemy's underestimate of the size of the earth, compared with the more accurate estimate of Eratosthenes – the equivalent of 500 stadia to the degree rather than 700. Given the difficulties of astronomical measures of longitude in classical times, most if not all of Ptolemy's values would have been obtained from distance measures and converted to longitude using the 500 value.[8]
Ancient Hindu astronomers were aware of the method of determining longitude from lunar eclipses, assuming a spherical earth. The method is described in the Sûrya Siddhânta, a Sanskrit treatise on Indian astronomy thought to date from the late 4th century or early 5th century CE.[9] Longitudes were referred to a prime meridian passing through Avantī, the modern Ujjain. Positions relative to this meridian were expressed in terms of length or time differences, but degrees were not used in India at this time. It is not clear whether this method was put into practice.
Islamic scholars knew the work of Ptolemy from at least the 9th century CE, when the first translation of his Geography into Arabic was made. He was held in high regard, although his errors were known.[10] One of their developments was to add more locations to Ptolemy's geographical tables with latitudes and longitudes, and in some cases improving the accuracy.[11] The methods used to determine most of the longitudes are not given, but a few accounts do give details. Simultaneous observations of two lunar eclipses at two locations were recorded by al-Battānī in 901, comparing Antakya with Raqqa, determining the difference in longitude between the two cities with an error less than 1°. This is considered the best that can be achieved with the methods then available – observation of the eclipse with the naked eye, and determination of local time using an astrolabe to measure the altitude of a suitable "clock star".[12][13] Al-Bīrūnī, early in the 11th century CE, also used eclipse data, but developed an alternative method involving an early form of triangulation. For two locations differing in both longitude and latitude, if the latitudes and the distance between them are known, as well as the size of the earth, it is possible to calculate the difference in longitude. With this method, al-Bīrūnī estimated the longitude difference between Baghdad and Ghazni using distance estimates from travellers over two different routes (and with a somewhat arbitrary adjustment for the crookedness of the roads). His result for the longitude difference between the two cities differs by about 1° from the modern value.[14] Mercier (1992) notes that this is a substantial improvement over Ptolemy, and that a comparable further improvement in accuracy would not occur until the 17th century in Europe.[14]: 188
While knowledge of Ptolemy (and more generally of Greek science and philosophy) was growing in the Islamic world, it was declining in Europe. John Kirtland Wright's (1925) summary is bleak: "We may pass over the mathematical geography of the Christian period [in Europe] before 1100; no discoveries were made, nor were there any attempts to apply the results of older discoveries. ... Ptolemy was forgotten and the labors of the Arabs in this field were as yet unknown".[15]: 65 Not all was lost or forgotten; Bede in his De naturum rerum affirms the sphericity of the earth. But his arguments are those of Aristotle, taken from Pliny. Bede adds nothing original.[16][17]
There is more of note in the later medieval period. Wright (1923) cites a description by Walcher of Malvern of a lunar eclipse in Italy (October 19, 1094), which occurred shortly before dawn. On his return to England, he compared notes with other monks to establish the time of their observation, which was before midnight. The comparison was too casual to allow a measurement of longitude differences, but the account shows that the principle was still understood.[18]: 81 In the 12th century, astronomical tables were prepared for a number of European cities, based on the work of al-Zarqālī in Toledo. These had to be adapted to the meridian of each city, and it is recorded that the lunar eclipse of September 12, 1178 was used to establish the longitude differences between Toledo, Marseilles, and Hereford.[18]: 85 The Hereford tables also added a list of over 70 locations, many in the Islamic world, with their longitudes and latitudes. These represent a great improvement on the similar tabulations of Ptolemy. For example, the longitudes of Ceuta and Tyre are given as 8° and 57° (east of the meridian of the Canary Islands), a difference of 49°, compared to the modern value of 40.5°, an overestimate of less than 20%.[18]: 87–88 In general, the later medieval period showed increasing interest in geography, and a willingness to make observations stimulated by an increase in travel (including pilgrimages and the Crusades) and by the availability of Islamic sources from Spain and North Africa[19][20] At the end of the medieval period, Ptolemy's work became directly available with the translations made in Florence at the end of the 14th and beginning of the 15th century.[21]
The 15th and 16th centuries were the time of Portuguese and Spanish voyages of discovery and conquest. In particular, the arrival of Europeans in the New World led to questions of where they actually were. Christopher Columbus made two attempts to discover his longitude by observing lunar eclipses. The first was on Saona Island, now in the Dominican Republic, during his second voyage. He wrote: "In the year 1494, when I was in Saona Island, which stands at the eastern tip of Española island [i.e. Hispaniola], there was a lunar eclipse on September the 14th, and we noticed that there was a difference of more than five hours and a half between there [Saona] and Cape S.Vincente, in Portugal".[22] He was unable to compare his observations with ones in Europe, and it is assumed that he used astronomical tables for reference. The second attempt was on the north coast of Jamaica on February 29, 1504, during his fourth voyage. His results were highly inaccurate, with longitude errors of 13 and 38° W respectively.[23] Randles (1985) documents longitude measurement by the Portuguese and Spanish between 1514 and 1627 both in the Americas and Asia, with errors ranging from 2° to 25°.[24]
Telescopes and clocks
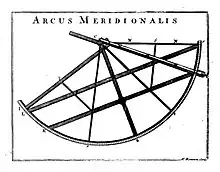
In 1608 a patent was submitted to the government in the Netherlands for a refracting telescope. The idea was picked up by, among others, Galileo who made his first telescope the following year, and began his series of astronomical discoveries that included the satellites of Jupiter, the phases of Venus, and the resolution of the Milky Way into individual stars. Over the next half century, improvements in optics and the use of calibrated mountings, optical grids, and micrometers to adjust positions transformed the telescope from an observation device to an accurate measurement tool.[26][27][28][29] It also greatly increased the range of events that could be observed to determine longitude.
The second important technical development for longitude determination was the pendulum clock, patented by Christiaan Huygens in 1657.[30] This gave an increase in accuracy of about 30-fold over previous mechanical clocks – the best pendulum clocks were accurate to about 10 seconds per day.[31] From the start, Huygens intended his clocks to be used for determination of longitude at sea.[32][33] However, pendulum clocks did not tolerate the motion of a ship sufficiently well, and after a series of trials it was concluded that other approaches would be needed. The future of pendulum clocks would be on land. Together with telescopic instruments, they would revolutionise observational astronomy and cartography in the coming years.[34] Huygens was also the first to use a balance spring as oscillator in a working clock, and this allowed accurate portable timepieces to be made. But it was not until the work of John Harrison that such clocks became accurate enough to be used as marine chronometers.[35]
Methods of determining longitude
The development of the telescope and accurate clocks increased the range of methods that could be used to determine longitude. With one exception (magnetic declination) they all depend on a common principle, which was to determine an absolute time from an event or measurement and to compare the corresponding local time at two different locations. (Absolute here refers to a time that is the same for an observer anywhere on Earth.) Each hour of difference of local time corresponds to a 15 degrees change of longitude (360 degrees divided by 24 hours).
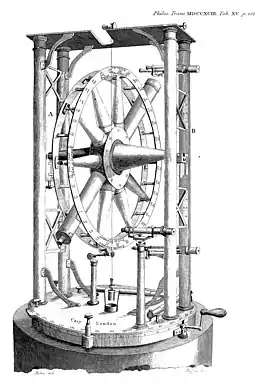
Local noon is defined as the time at which the Sun is at the highest point in the sky. This is hard to determine directly, as the apparent motion of the Sun is nearly horizontal at noon. The usual approach was to take the mid-point between two times at which the Sun was at the same altitude. With an unobstructed horizon, the mid-point between sunrise and sunset could be used.[36] At night local time could be obtained from the apparent rotation of the stars around the celestial pole, either measuring the altitude of a suitable star with a sextant, or the transit of a star across the meridian using a transit instrument.[37]
To determine the measure of absolute time, lunar eclipses continued to be used. Other proposed methods included:
Lunar distances
This is the earliest proposal, having been first suggested in a letter by Amerigo Vespucci referring to observations he made in 1499.[38][39] The method was published by Johannes Werner in 1514,[40] and discussed in detail by Petrus Apianus in 1524.[41] The method depends on the motion of the Moon relative to the "fixed" stars, which completes a 360° circuit in 27.3 days on average (a lunar month), giving an observed movement of just over 0.5°/hour. Thus an accurate measurement of the angle is required, since 2 minute of arc (1/30°) difference in the angle between the Moon and the selected star corresponds to a 1°.0' difference in the longitude: 60 nautical miles (110 km) at the equator.[42] The method also required accurate tables, which were complex to construct, since they had to take into account parallax and the various sources of irregularity in the orbit of the Moon. Neither measuring instruments nor astronomical tables were accurate enough in the early 16th century. Vespucci's attempt to use the method placed him at 82° West of Cadiz, when he was actually less than 40° West of Cadiz, on the north coast of Brazil.[38]
Satellites of Jupiter
Galileo discovered the four brightest moon of Jupiter, Io, Europa, Ganymede and Callisto in 1610. Having determined their orbital periods, he proposed in 1612 that with sufficiently accurate knowledge of their orbits one could use their positions as a universal clock, which would make possible the determination of longitude. Galileo applied for Spain's lucrative prize for solutions to the longitude problem in 1616. He worked on this problem from time to time, but was unable to convince the Spanish court. He later applied to Holland for their prize, but by then he had been tried for heresy by the Roman Inquisition and sentenced to house arrest for the rest of his life.[43]: 15–16

Galileo's method required a telescope, as the moons are not visible to the naked eye. For use in marine navigation, Galileo proposed the celatone, a device in the form of a helmet with a telescope mounted so as to accommodate the motion of the observer on the ship.[44] This was later replaced with the idea of a pair of nested hemispheric shells separated by a bath of oil. This would provide a platform that would allow the observer to remain stationary as the ship rolled beneath him, in the manner of a gimballed platform. To provide for the determination of time from the observed moons' positions, a jovilabe was offered; this was an analogue computer that calculated time from the positions and that got its name from its similarities to an astrolabe.[45] The practical problems were severe and the method was never used at sea.
On land, this method proved useful and accurate. In 1668, Giovanni Domenico Cassini published detailed tables of Jupiter's moons.[43]: 21 An early use was the measurement of the longitude of the site of Tycho Brahe's former observatory on the island of Hven. Jean Picard on Hven and Cassini in Paris made observations during 1671 and 1672, and obtained a value of 42 minutes 10 seconds (time) east of Paris, corresponding to 10° 32' 30", about 12 minute of arc (1/5°) higher than the modern value.[46]
Jupiter's moons provided time information for the French Académie des Sciences' project to survey France that produced a new map in 1744 which showed the coastline was significantly further east than on previous maps.[47]
Appulses and occultations
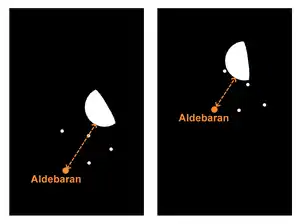
Two proposed methods depend on the relative motions of the Moon and a star or planet. An appulse is the least apparent distance between the two objects, an occultation occurs when the star or planet passes behind the Moon – essentially a type of eclipse. The times of either of these events can be used as the measure of absolute time in the same way as with a lunar eclipse. Edmond Halley described the use of this method to determine the longitude of Balasore in India, using observations of the star Aldebaran (the "Bull's Eye", being the brightest star in the constellation Taurus) in 1680, with an error of just over half a degree.[48] He published a more detailed account of the method in 1717.[49] A longitude determination using the occultation of a planet, Jupiter, was described by James Pound in 1714.[50] The 1769 transit of Venus provided an opportunity for determining accurate longitude of over 100 seaports around the world.[43]: 73
Chronometers
The first to suggest travelling with a clock to determine longitude, in 1530, was Gemma Frisius, a physician, mathematician, cartographer, philosopher, and instrument maker from the Netherlands. The clock would be set to the local time of a starting point whose longitude was known, and the longitude of any other place could be determined by comparing its local time with the clock time.[51][52]: 259 While the method is perfectly sound, and was partly stimulated by recent improvements in the accuracy of mechanical clocks, it still requires far more accurate time-keeping than was available in Frisius's day. The term chronometer was not used until the following century,[53] and it would be over two centuries before this became the standard method for determining longitude at sea.[54]
Magnetic declination
This method is based on the observation that a compass needle does not in general point exactly north. The angle between true north and the direction of the compass needle (magnetic north) is called the magnetic declination or variation, and its value varies from place to place. Several writers proposed that the size of magnetic declination could be used to determine longitude. Mercator suggested that the magnetic north pole was an island in the longitude of the Azores, where magnetic declination was, at that time, close to zero. These ideas were supported by Michiel Coignet in his Nautical Instruction.[52]
Halley made extensive studies of magnetic variation during his voyages on the pink Paramour. He published the first chart showing isogonic lines – lines of equal magnetic declination – in 1701.[55] One of the purposes of the chart was to aid in determining longitude, but the method was eventually to fail as changes in magnetic declination over time proved too large and too unreliable to provide a basis for navigation.
Land and sea

Measurements of longitude on land and sea complemented one another. As Edmond Halley pointed out in 1717, "But since it would be needless to enquire exactly what longitude a ship is in, when that of the port to which she is bound is still unknown it were to be wisht that the princes of the earth would cause such observations to be made, in the ports and on the principal head-lands of their dominions, each for his own, as might once for all settle truly the limits of the land and sea."[49] But determinations of longitude on land and sea did not develop in parallel.
On land, the period from the development of telescopes and pendulum clocks until the mid-18th century saw a steady increase in the number of places whose longitude had been determined with reasonable accuracy, often with errors of less than a degree, and nearly always within 2–3°. By the 1720s errors were consistently less than 1°.[56]
At sea during the same period, the situation was very different. Two problems proved intractable. The first was the need for immediate results. On land, an astronomer at, say, Cambridge Massachusetts could wait for the next lunar eclipse that would be visible both at Cambridge and in London; set a pendulum clock to local time in the few days before the eclipse; time the events of the eclipse; send the details across the Atlantic and wait weeks or months to compare the results with a London colleague who had made similar observations; calculate the longitude of Cambridge; then send the results for publication, which might be a year or two after the eclipse.[57] And if either Cambridge or London had no visibility because of cloud, wait for the next eclipse. The marine navigator needed the results quickly. The second problem was the marine environment. Making accurate observations in an ocean swell is much harder than on land, and pendulum clocks do not work well in these conditions. Thus longitude at sea could only be estimated from dead reckoning (DR) – by using estimations of speed and course from a known starting position – at a time when longitude determination on land was becoming increasingly accurate.
To compensate for longitude uncertaintly, navigators have sometimes relied on their accurate knowledge of latitude. They would sail to the latitude of their destination, then sail toward it along a line of constant latitude, known as running down a westing (if westbound, easting otherwise).[58] However, the latitude line was usually slower than the most direct or most favorable route, extending the voyage by days or weeks and increasing the risk of short rations, scurvy, and starvation.[59]
A famous longitude-error disaster occurred in April 1741. George Anson, commanding HMS Centurion, was rounding Cape Horn east to west. Believing himself past the Cape, he turned to the north but soon found himself headed straight towards land. A particularly strong easterly current had put him well to the east of his dead-reckoning position, and he had to resume his westerly course for several days. When finally past the Horn, he headed north for the Juan Fernández Islands to take on supplies for his crew, many of whom were sick with scurvy. On reaching the latitude of Juan Fernández, he did not know whether the islands were to the east or west, and spent 10 days sailing first eastwards and then westwards before finally reaching the islands. During this time over half of the ship's company died of scurvy.[35][60]
Government initiatives
In response to the problems of navigation, a number of European maritime powers offered prizes for a method to determine longitude at sea. Philip II of Spain was the first, offering a reward for a solution in 1567; his son, Philip III, increased the reward in 1598 to 6000 gold ducats plus a permanent pension of 2,000 gold ducats a year.[43]: 15 Holland offered 30,000 florins in the early 17th century. Neither of these prizes produced a solution,[61]: 9 though Galileo applied for both.[43]: 16

The second half of the 17th century saw the foundation of official observatories in Paris and London. The Paris Observatory was founded in 1667 under the auspices of the French Académie des Sciences. The Observatory building south of Paris was completed in 1672.[62] Early astronomers included Jean Picard, Christiaan Huygens, and Dominique Cassini.[63]: 165–177 It was not intended for any specific project, but soon became involved in the survey of France that led (after many delays due to wars and unsympathetic ministries) to the Academy's first map of France in 1744. The survey used a combination of triangulation and astronomical observations, with the satellites of Jupiter used to determine longitude. By 1684, sufficient data had been obtained to show that previous maps of France had a major longitude error, showing the Atlantic coast too far to the west. In fact France was found to be substantially smaller than previously thought.[64][65] (Louis XIV commented that they had taken more territory from France than he had gained in all his wars.)
The Royal Observatory in Greenwich east of London, founded in 1675, a few years after the Paris Observatory, was established explicitly to address the longitude problem.[66] John Flamsteed, the first Astronomer Royal, was instructed to "apply himself with the utmost care and diligence to the rectifying the tables of the motions of the heavens and the places of the fixed stars, so as to find out the so-much-desired longitude of places for the perfecting the art of navigation".[67]: 268 [29] The initial work was in cataloguing stars and their position, and Flamsteed created a catalogue of 3,310 stars, which formed the basis for future work.[67]: 277
While Flamsteed's catalogue was important, it did not in itself provide a solution. In 1714, the British Parliament passed "An Act for providing a public Reward for such Person or Persons as shall discover the Longitude at Sea" (13 Ann. c. 14), and set up a board to administer the award. The payout depended on the accuracy of the method: from £10,000 (equivalent to £1,538,000 in 2021)[68] for an accuracy within one degree of longitude (60 nautical miles (110 km) at the equator) to £20,000 (equivalent to £3,076,000 in 2021)[68] for accuracy within one half degree.[61]: 9
This prize in due course produced two workable solutions. The first was lunar distances, which required careful observation, accurate tables, and rather lengthy calculations. Tobias Mayer had produced tables based on his own observations of the moon, and submitted these to the Board in 1755. These observations were found to give the required accuracy, although the lengthy calculations required (up to four hours) were a barrier to routine use. Mayer's widow in due course received an award from the Board.[69] Nevil Maskelyne, the newly appointed Astronomer Royal who was on the Board of Longitude, started with Mayer's tables and after his own experiments at sea trying out the lunar distance method, proposed annual publication of pre-calculated lunar distance predictions in an official nautical almanac for the purpose of finding longitude at sea. Being very enthusiastic for the lunar distance method, Maskelyne and his team of computers worked feverishly through the year 1766, preparing tables for the new Nautical Almanac and Astronomical Ephemeris. Published first with data for the year 1767, it included daily tables of the positions of the Sun, Moon, and planets and other astronomical data, as well as tables of lunar distances giving the distance of the Moon from the Sun and nine stars suitable for lunar observations (ten stars for the first few years).[70][71][72] This publication later became the standard almanac for mariners worldwide. Since it was based on the Royal Observatory, it helped lead to the international adoption a century later of the Greenwich Meridian as an international standard.
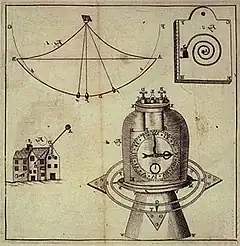
The second method was the use of a chronometer. Many, including Isaac Newton, were pessimistic that a clock of the required accuracy could ever be developed. The Earth turns by one degree of longitude in four minutes,[73] so the maximum acceptable timekeeping error is a few seconds per day. At that time, there were no clocks that could come close to such accuracy under the conditions of a moving ship. John Harrison, a Yorkshire carpenter and clock-maker, spent over three decades in proving it could be done.[61]: 14–27
Harrison built five chronometers, two of which were tested at sea. His first, H-1, was sent on a preliminary test by the Admiralty, a voyage to Lisbon and back. It lost considerable time on the outward voyage but performed excellently on the return leg, which was not part of the official trial. The perfectionist in Harrison prevented him from sending it on the Board of Longitude's official test voyage to the West Indies (and in any case it was regarded as too large and impractical for service use). He instead embarked on the construction of H-2, immediately followed by H-3. During construction of H-3, Harrison realised that the loss of time of the H-1 on the Lisbon outward voyage was due to the mechanism losing time whenever the ship came about to tack down the English Channel. Inspired by this realisation, Harrison produced H-4 with a completely different mechanism. The H-4 sea trial in 1762 satisfied all the requirements for the Longitude Prize. However, the board withheld the prize, and Harrison was forced to fight for his reward, finally receiving payment in 1773 after the intervention of Parliament.[61]: 26
The French were also very interested in the problem of longitude, and the French Academy examined proposals and also offered prize money, particularly after 1748.[74]: 160 Initially the assessors were dominated by the astronomer Pierre Bouguer who was opposed to the idea of chronometers, but after his death in 1758 both astronomical and mechanical approaches were considered. Two clock-makers dominated, Ferdinand Berthoud and Pierre Le Roy. Four sea trials took place between 1767 and 1772, evaluating lunar distances as well as a variety of time-keepers. Results for both approaches steadily improved as the trials proceeded, and both methods were deemed suitable for use in navigation.[74]: 163–174
Lunar distances versus chronometers
Although both chronometers and lunar distances had been shown to be practicable methods for determining longitude, it was some while before either became widely used. In the early years, chronometers were very expensive, and the calculations required for lunar distances were still complex and time-consuming, in spite of Maskelyne's work to simplify them. Both methods were initially used mainly in specialist scientific and surveying voyages. On the evidence of ships' logbooks and nautical manuals, lunar distances started to be used by ordinary navigators in the 1780s, and became common after 1790.[75]
While chronometers could deal with the conditions of a ship at sea, they could be vulnerable to the harsher outdoor conditions of land-based exploration and surveying, for example in the American North-West, and lunar distances were the main method used by surveyors such as David Thompson.[76] Between January and May 1793 he took 34 observations at Cumberland House, Saskatchewan, obtaining a mean value of 102° 12' W, about 2' (2.2 km) east of the modern value.[77] Each of the 34 observations would have required about 3 hours of calculation. These lunar distance calculations became substantially simpler in 1805, with the publication of tables using the Haversine formula by Josef de Mendoza y Ríos.[78]
The advantage of using chronometers was that though astronomical observations were still needed to establish local time, the observations were simpler and less demanding of accuracy. Once local time had been established, and any necessary corrections made to the chronometer time, the calculation to obtain longitude was straightforward. A contemporary guide to the method was published by William Wales in 1794.[79] The disadvantage of cost gradually became less as chronometers began to be made in quantity. The chronometers used were not those of Harrison. Other makers such as Thomas Earnshaw, who developed the spring detent escapement,[80] simplified chronometer design and production. From 1800 to 1850, as chronometers became more affordable and reliable, they increasingly displaced the lunar distance method.

Chronometers needed to be checked and reset at intervals. On short voyages between places of known longitude this was not a problem. For longer journeys, particularly of survey and exploration, astronomical methods continued to be important. An example of the way chronometers and lunars complemented one another in surveying work is Matthew Flinders' circumnavigation of Australia in 1801–3. Surveying the south coast, Flinders started at King George Sound, a known location from George Vancouver's earlier survey. He proceeded along the south coast, using chronometers to determine longitude of the features along the way. Arriving at the bay he named Port Lincoln, he set up a shore observatory, and determined the longitude from thirty sets of lunar distances. He then determined the chronometer error, and recalculated all the longitudes of the intervening locations.[81]
Ships often carried more than one chronometer. Two would give dual modular redundancy, allowing a backup if one should cease to work, but not allowing any error correction if the two displayed a different time, since it would be impossible to know which one was wrong: the error detection obtained would be the same as having only one chronometer and checking it periodically: every day at noon against dead reckoning. Three chronometers provided triple modular redundancy, allowing error correction if one of the three was wrong, so the pilot would take the average of the two with closer readings (average precision vote). This inspired the adage: "Never go to sea with two chronometers; take one or three."[82] Some vessels carried more than three chronometers – for example, HMS Beagle carried 22 chronometers.[83]
By 1850, the vast majority of ocean-going navigators worldwide had abandoned the method of lunar distances. Nonetheless, expert navigators continued to learn lunars as late as 1905, though for most this was only a textbook exercise required for certain licenses. Littlehales noted in 1909: "The lunar-distance tables were omitted from the Connaissance des Temps for the year 1905, after having retained their place in the French official ephemeris for 131 years; and from the British Nautical Almanac for 1907, after having been presented annually since the year 1767, when Maskelyne's tables were published."[84]
Land surveying and telegraphy
Surveying on land continued to use a mixture of triangulation and astronomical methods, to which was added the use of chronometers once they became readily available. An early use of chronometers in land surveying was reported by Simeon Borden in his survey of Massachusetts in 1846. Having checked Nathaniel Bowditch's value for the longitude of the State House in Boston he determined the longitude of the First Congregational Church at Pittsfield, transporting 38 chronometers on 13 excursions between the two locations.[85] Chronometers were also transported much longer distances. For example, the US Coast Survey organised expeditions in 1849 and 1855 in which a total of over 200 chronometers were shipped between Liverpool and Boston, not for navigation, but to obtain a more accurate determination of the longitude of the Observatory at Cambridge, Massachusetts, and thus to anchor the US Survey to the Greenwich meridian.[86]: 5
The first working telegraphs were established in Britain by Wheatstone and Cooke in 1839, and in the US by Morse in 1844. The idea of using the telegraph to transmit a time signal for longitude determination was suggested by François Arago to Morse in 1837,[87] and the first test of this idea was made by Capt. Wilkes of the U.S. Navy in 1844, over Morse's line between Washington and Baltimore. Two chronometers were synchronized, and taken to the two telegraph offices to check that time was accurately transmitted.[88]
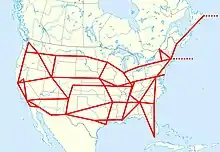
The method was soon in practical use for longitude determination, in particular by the U.S. Coast Survey, and over longer and longer distances as the telegraph network spread across North America. Many technical challenges were dealt with. Initially operators sent signals manually and listened for clicks on the line and compared them with clock ticks, estimating fractions of a second. Circuit breaking clocks and pen recorders were introduced in 1849 to automate these process, leading to great improvements in both accuracy and productivity.[90]: 318–330 [91]: 98–107 With the establishment of an observatory in Quebec in 1850 under the direction of Edward David Ashe, a network of telegraphic longitude determinations was carried out for eastern Canada, and linked to that of Harvard and Chicago.[92][93]
.jpeg.webp)
A big expansion to the "telegraphic net of longitude" was due to the successful completion of the transatlantic telegraph cable between S.W. Ireland and Nova Scotia in 1866.[86] A cable from Brest in France to Duxbury Massachusetts was completed in 1870, and gave the opportunity to check results by a different route. In the interval, the land-based parts of the network had improved, including the elimination of repeaters. Comparisons of the difference between Greenwich and Cambridge Massachusetts showed differences between measurement of 0.01 second of time, with a probable error of ±0.04 seconds, equivalent to 45 feet.[91]: 175 Summing up the net in 1897, Charles Schott presented a table of the major locations throughout the United States whose locations had been determined by telegraphy, with the dates and pairings, and the probable error.[89][94] The net was expanded into the American North-West with telegraphic connection to Alaska and western Canada. Telegraphic links between Dawson City, Yukon, Fort Egbert, Alaska, and Seattle and Vancouver were used to provide a double determination of the position of the 141st meridian where it crossed the Yukon River, and thus provide a starting point for a survey of the border between the US and Canada to north and south during 1906–1908[95][96] William Bowie has given a detailed description of the telegraphic method as used by the U.S.Coast and Geodetic Survey.[97]
The U.S. Navy expanded the web into the West Indies and Central and South America in four expeditions in the years 1874–90. One series of observations linked Key West, Florida with the West Indies and Panama City.[99] A second covered locations in Brazil and Argentina, and also linked to Greenwich via Lisbon.[100] The third ran from Galveston, Texas, through Mexico and Central America, including Panama, and on to Peru and Chile, connecting to Argentina via Cordoba.[98] The fourth added locations in Mexico, Central America and the West Indies, and extended the chain to Curaçao and Venezuela.[101]
East of Greenwich, telegraphic determinations of longitude were made of locations in Egypt, including Suez, as part of the observations of the 1874 transit of Venus directed by Sir George Airy, the British Astronomer Royal.[102][103] Telegraphic observations made as part of the Great Trigonometrical Survey of India, including Madras, were linked to Aden and Suez in 1877.[104][103] In 1875, the longitude of Vladivostok in eastern Siberia was determined by telegraphic connection with Saint Petersburg. The US Navy used Suez, Madras and Vladivostok as the anchor-points for a chain of determinations made in 1881–1882, which extended through Japan, China, the Philippines, and Singapore.[105]
The telegraphic web circled the globe in 1902 with the connection of Australia and New Zealand to Canada via the All Red Line. This allowed a double determination of longitudes from east and west, which agreed within one second of arc (1/15 second of time).[106]
The telegraphic net of longitude was less important in Western Europe, which had already mostly been surveyed in detail using triangulation and astronomical observations. But the "American Method" was used in Europe, for example in a series of measurements to determine the longitude difference between the observatories of Greenwich and Paris with greater accuracy than previously available.[107]
Wireless methods
Marconi was granted his patent for wireless telegraphy in 1897.[108] The potential for using wireless time signals for determining longitude was soon apparent.[109]
Wireless telegraphy was used to extend and refine the telegraphic web of longitude, giving potentially greater accuracy, and reaching locations that were not connected to the wired telegraph network. An early determination was that between Potsdam and The Brocken in Germany, a distance of about 100 miles (160 km), in 1906.[110] In 1911 the French determined the difference of longitude between Paris and Bizerte in Tunisia, a distance of 920 miles (1,480 km), and in 1913–14 a transatlantic determination was made between Paris and Washington.[111]
The first wireless time signals for the use of ships at sea started in 1907, from Halifax, Nova Scotia.[112] Time signals were transmitted from the Eiffel Tower in Paris starting in 1910.[113] These signals allowed navigators to check and adjust their chronometers on a frequent basis.[114][115] An international conference in 1912 allocated times for various wireless stations around the world to transmit their signals, allowing for near-worldwide coverage without interference between stations.[113] Wireless time-signals were also used by land-based observers in the field, in particular surveyors and explorers.[116]
Radio navigation systems came into general use after World War II. Several systems were developed including the Decca Navigator System, the US coastguard LORAN-C, the international Omega system, and the Soviet Alpha and CHAYKA. The systems all depended on transmissions from fixed navigational beacons. A ship-board receiver calculated the vessel's position from these transmissions.[117] These systems were the first to allow accurate navigation when astronomical observations could not be made because of poor visibility, and became the established method for commercial shipping until the introduction of satellite-based navigation systems in the early 1990s.
In 1908, Nikola Tesla had predicted:
In the densest fog or darkness of night, without a compass or other instruments of orientation, or a timepiece, it will be possible to guide a vessel along the shortest or orthodromic path, to instantly read the latitude and longitude, the hour, the distance from any point, and the true speed and direction of movement.[118]
His prediction was fulfilled partially with radio navigation systems, and completely with computer geopositioning systems based on GPS satellite beacons.
References
- Roller, Duane W. (2010). Eratosthenes' Geography. Princeton, N.J.: Princeton University Press. pp. 25–26. ISBN 978-1400832217. Retrieved April 17, 2020.
- Dicks, D.R. (1953). Hipparchus : a critical edition of the extant material for his life and works (PhD). Birkbeck College, University of London.
- Hoffman, Susanne M. (2016). "How time served to measure the geographical position since Hellenism". In Arias, Elisa Felicitas; Combrinck, Ludwig; Gabor, Pavel; Hohenkerk, Catherine; Seidelmann, P.Kenneth (eds.). The Science of Time. Astrophysics and Space Science Proceedings. Vol. 50. Springer International. pp. 25–36. doi:10.1007/978-3-319-59909-0_4. ISBN 978-3-319-59908-3.
- Bunbury, E.H. (1879). A History of Ancient Geography. Vol. 2. London: John Murray.
- Snyder, John P (1987). Map Projections – A working manual. Washington, D.C.: US Geological Survey.
- Mittenhuber, Florian (2010). "The Tradition of Texts and Maps in Ptolemy's Geography". In Jones, Alexander (ed.). Ptolemy in Perspective: Use and Criticism of his Work from Antiquity to the Nineteenth Century. Archimedes. Vol. 23. Dordrecht: Springer. pp. 95-119. doi:10.1007/978-90-481-2788-7_4. ISBN 978-90-481-2787-0.
- Shcheglov, Dmitry A. (2016). "The Error in Longitude in Ptolemy's Geography Revisited". The Cartographic Journal. 53 (1): 3–14. doi:10.1179/1743277414Y.0000000098. S2CID 129864284.
- Russo, Lucio (2013). "Ptolemy's longitudes and Eratosthenes' measurement of the earth's circumference". Mathematics and Mechanics of Complex Systems. 1 (1): 67–79. doi:10.2140/memocs.2013.1.67.
- Burgess, Ebenezer (1935). Translation of the Surya Siddhanta a text-book of Hindu astronomy with notes and appendix. University of Calcutta. pp. 45–48.
- Ragep, F.Jamil (2010). "Islamic reactions to Ptolemy's imprecisions". In Jones, A. (ed.). Ptolemy in Perspective. Archimedes. Vol. 23. Dordrecht: Springer. doi:10.1007/978-90-481-2788-7. ISBN 978-90-481-2788-7.
- Tibbetts, Gerald R. (1992). "The Beginnings of a Cartographic Tradition" (PDF). In Harley, J.B.; Woodward, David (eds.). The History of Cartography Vol. 2 Cartography in the Traditional Islamic and South Asian Societies. University of Chicago Press.
- Said, S.S.; Stevenson, F.R. (1997). "Solar and Lunar Eclipse Measurements by Medieval Muslim Astronomers, II: Observations". Journal for the History of Astronomy. 28 (1): 29–48. Bibcode:1997JHA....28...29S. doi:10.1177/002182869702800103. S2CID 117100760.
- Steele, John Michael (1998). Observations and predictions of eclipse times by astronomers in the pre-telescopic period (PhD). University of Durham (United Kingdom).
- Mercier, Raymond P. (1992). "Geodesy" (PDF). In Harley, J.B.; Woodward, David (eds.). The History of Cartography Vol. 2 Cartography in the Traditional Islamic and South Asian Societies. University of Chicago Press.
- Wright, John Kirtland (1925). The geographical lore of the time of the Crusades: A study in the history of medieval science and tradition in Western Europe. New York: American geographical society.
- Darby, H.C. (1935). "The geographical ideas of the Venerable Bede". Scottish Geographical Magazine. 51 (2): 84–89. doi:10.1080/00369223508734963.
- Friedman, John Block (2000). Trade, Travel and Exploration in the Middle Ages: An Encyclopedia. Taylor & Francis Ltd. p. 495. ISBN 0-8153-2003-5.
- Wright, John Kirtland (1923). "Notes on the Knowledge of Latitudes and Longitudes in the Middle Ages". Isis. 5 (1). Bibcode:1922nkll.book.....W.
- Beazley, C.Raymond (1901). The Dawn of Modern Geography, vol. I, London, 1897; A History of Exploration and Geographical Science from the Close of the Ninth to the Middle of the Thirteenth Century (c. AD 900–1260). London: John Murray.
- Lilley, Keith D. (2011). "Geography's medieval history: A neglected enterprise?". Dialogues in Human Geography. 1 (2): 147–162. doi:10.1177/2043820611404459. S2CID 128715649.
- Gautier Dalché, P. (2007). "The reception of Ptolemy's Geography (end of the fourteenth to beginning of the sixteenth century)". In Woodward, D. (ed.). The History of Cartography, Volume 3. Cartography in the European Renaissance, Part 1 (PDF). Chicago: University of Chicago Press. pp. 285–364.
- de Navarrete, Martín Fernández (1825). Coleccion de los viages y descubrimientos que hicieron por mar los Españoles, desde fines del siglo XV...: con varias documentos inéditos concernientes a la historia de la marina castellana y de los establecimientos españoles en Indias, Tomo II. Madrid: En la Imprenta Nacional. p. 272.
- Pickering, Keith (1996). "Columbus's Method of Determining Longitude: An Analytical View". The Journal of Navigation. 49 (1): 96–111. Bibcode:1996JNav...49...95P. doi:10.1017/S037346330001314X. S2CID 129232861.
- Randles, W.G.L. (1985). "Portuguese and Spanish attempts to measure longitude in the 16th century". Vistas in Astronomy. 28 (1): 235–241. Bibcode:1985VA.....28..235R. doi:10.1016/0083-6656(85)90031-5.
- Chapman, Allan (1976). "Astronomia practica: The principal instruments and their uses at the Royal Observatory". Vistas in Astronomy. 20: 141–156. Bibcode:1976VA.....20..141C. doi:10.1016/0083-6656(76)90025-8.
- Pannekoek, Anton (1989). A history of astronomy. Courier Corporation. pp. 259–276.
- Van Helden, Albert (1974). "The Telescope in the Seventeenth Century". Isis. 65 (1): 38–58. doi:10.1086/351216. JSTOR 228880. S2CID 224838258.
- Høg, Erik (2009). "400 years of astrometry: from Tycho Brahe to Hipparcos". Experimental Astronomy. 25 (1): 225–240. Bibcode:2009ExA....25..225H. doi:10.1007/s10686-009-9156-7. S2CID 121722096.
- Perryman, Michael (2012). "The history of astrometry". The European Physical Journal H. 37 (5): 745–792. arXiv:1209.3563. Bibcode:2012EPJH...37..745P. doi:10.1140/epjh/e2012-30039-4. S2CID 119111979.
- Grimbergen, Kees (2004). Fletcher, Karen (ed.). Huygens and the advancement of time measurements. Titan – From Discovery to Encounter. Titan – from Discovery to Encounter. Vol. 1278. ESTEC, Noordwijk, Netherlands: ESA Publications Division. pp. 91–102. Bibcode:2004ESASP1278...91G. ISBN 92-9092-997-9.
- Blumenthal, Aaron S.; Nosonovsky, Michael (2020). "Friction and Dynamics of Verge and Foliot: How the Invention of the Pendulum Made Clocks Much More Accurate". Applied Mechanics. 1 (2): 111–122. doi:10.3390/applmech1020008.
- Huygens, Christiaan (1669). "Instructions concerning the use of pendulum-watches for finding the longitude at sea". Philosophical Transactions. 4 (47): 937–953. Bibcode:1669RSPT....4..937.
- Howard, Nicole (2008). "Marketing Longitude: Clocks, Kings, Courtiers, and Christiaan Huygens". Book History. 11: 59–88. doi:10.1353/bh.0.0011. S2CID 161827238.
- Olmsted, J.W. (1960). "The Voyage of Jean Richer to Acadia in 1670: A Study in the Relations of Science and Navigation under Colbert". Proceedings of the American Philosophical Society. 104 (6): 612–634. JSTOR 985537.
- Gould, R.T. (1935). "John Harrison and his timekeepers". The Mariner's Mirror. 21 (2): 115–139. Bibcode:1935jhht.book.....G. doi:10.1080/00253359.1935.10658708.
- Norie, John William (1805). A New and Complete Epitome of Practical Navigation. William Heather: William Heather. p. 219.
- Wollaston, Francis (1793). "A description of a transit circle, for determining the place of celestial objects as they pass the meridian". Philosophical Transactions. 83: 133–153.
- Cited in: Arciniegas, German (1955). Amerigo And The New World The Life & Times Of Amerigo Vespucci. New York: Alfred A. Knopf. p. 192.
- Pohl, Frederick Julius (1966). Amerigo Vespucci : pilot major. New York: Octagon Books. p. 80.
- Werner, Johann (1514). In hoc opere haec continentur Noua translatio primi libri Geographiae Cl. Ptolomaei (in Latin). Nurembergae: Ioanne Stuchs.
- Apianus, Petrus (1533). Cosmographicus liber Petri Apiani mathematici, iam denuo integritati restitutus per Gemmam Phrysium (in Latin). Landshut: vaeneunt in pingui gallina per Arnoldum Birckman.
- Halley, Edmund (1731). "A Proposal of a Method for Finding the Longitude at Sea within a Degree, or Twenty Leagues". Philosophical Transactions. 37 (417–426): 185–195.
- Edwin Danson (2006). Weighing the World. Qxford University Press. ISBN 0-19-518169-7.
- Celatone
- Jovilabe
- Picard, Jean (1729). "Voyage D'Uranibourg ou Observations Astronomiques faites en Dannemarck". Mémoires de l'Académie Royale des Sciences (in French). 7 (1): 223–264.
- "Solving Longitude: Jupiter's Moons". Royal Museums Greenwich. October 16, 2014.
- Halley, Edmund (1682). "An account of some very considerable observations made at Ballasore in India, serving to find the longitude of that place, and rectifying very great errours in some famous modern geographers". Philosophical Collections of the Royal Society of London. 5 (1): 124–126. doi:10.1098/rscl.1682.0012.
- Halley, Edmund (1717). "An advertisement to astronomers, of the advantages that may accrue from the observation of the moon's frequent appulses to the Hyades, during the next three ensuing years". Philosophical Transactions. 30 (354): 692–694.
- Pound, James (1714). "Some late curious astronomical observations communicated by the Reverend and learned Mr. James Pound, Rector of Wansted". Philosophical Transactions of the Royal Society of London. 29 (347): 401–405.
- Pogo, A (1935). "Gemma Frisius, His Method of Determining Differences of Longitude by Transporting Timepieces (1530), and His Treatise on Triangulation (1533)". Isis. 22 (2): 469–506. doi:10.1086/346920. S2CID 143585356.
- Meskens, Ad (1992). "Michiel Coignet's Nautical Instruction". The Mariner's Mirror. 78 (3): 257–276. doi:10.1080/00253359.1992.10656406.
- Koberer, Wolfgang (2016). "On the First Use of the Term "Chronometer"". The Mariner's Mirror. 102 (2): 203–206. doi:10.1080/00253359.2016.1167400. S2CID 164165009.
- Gould, Rupert T (1921). "The History of the Chronometer". The Geographical Journal. 57 (4): 253–268. doi:10.2307/1780557. JSTOR 1780557.
- Halley, Edm. (1701). A New and Correct Chart Shewing the Variations of the Compass in the Western & Southern Oceans as Observed in ye Year 1700 by his Ma[jes]ties Command. London: Mount and Page.
- See, for example, Port Royal, Jamaica: Halley, Edmond (1722). "Observations on the Eclipse of the Moon, June 18, 1722. and the Longitude of Port Royal in Jamaica". Philosophical Transactions. 32 (370–380): 235–236.; Buenos Aires: Halley, Edm. (1722). "The Longitude of Buenos Aires, Determin'd from an Observation Made There by Père Feuillée". Philosophical Transactions. 32 (370–380): 2–4.Santa Catarina, Brazil: Legge, Edward; Atwell, Joseph (1743). "Extract of a letter from the Honble Edward Legge, Esq; F. R. S. Captain of his Majesty's ship the Severn, containing an observation of the eclipse of the moon, Dec. 21. 1740. at the Island of St. Catharine on the Coast of Brasil". Philosophical Transactions. 42 (462): 18–19.
- Brattle, Tho.; Hodgson, J. (1704). "An Account of Some Eclipses of the Sun and Moon, Observed by Mr Tho. Brattle, at Cambridge, about Four Miles from Boston in New-England, Whence the Difference of Longitude between Cambridge and London is Determin'd, from an Observation Made of One of Them at London". Philosophical Transactions. 24: 1630–1638.
- Dutton's Navigation and Piloting, 12th edition. G.D. Dunlap and H.H. Shufeldt, eds. Naval Institute Press 1972, ISBN 0-87021-163-3
- As food stores ran low, the crew would be put on rations to extend the time with food This was referred to as giving the crew short rations, short allowance or petty warrant.
- Somerville, Boyle (1934). Commander Anson's World Voyage. London: Heinemann. pp. 46–56.
- Siegel, Jonathan R. (2009). "Law and Longitude". Tulane Law Review. 84: 1–66.
- Wolf, Charles (1902). Histoire de l'Observatoire de Paris de sa fondation à 1793 (in French). Paris: Gauthier-Villars.
- Wolf, A. (1935). History Of Science, Technology And Philosophy: In The 16th And 17th Centuries Volume.1. London: George Allen & Unwin.
- Gallois, L. (1909). "L'Académie des Sciences et les Origines de la Carte de Cassini: Premier article". Annales de Géographie (in French). 18 (99): 193–204. doi:10.3406/geo.1909.6695. JSTOR 23436957.
- Picard, Jean; de la Hire, Philippe (1729). "Pour la Carte de France corrigée sur les Observations de MM. Picard & de la Hire". Mémoires de l'Académie des Sciences (in French). 7 (7).
- Major, F. G. (2014). "The Longitude Problem". Quo Vadis: Evolution of Modern Navigation: The Rise of Quantum Techniques. New York: Springer. pp. 113–129. doi:10.1007/978-1-4614-8672-5_6. ISBN 978-1-4614-8671-8.
- Carpenter, James (1872). "Greenwich Observatory". The Popular Science Review. 11 (42): 267–282.
- UK Retail Price Index inflation figures are based on data from Clark, Gregory (2017). "The Annual RPI and Average Earnings for Britain, 1209 to Present (New Series)". MeasuringWorth. Retrieved June 11, 2022.
- Forbes, Eric Gray (2006). "Tobias Mayer's lunar tables". Annals of Science. 22 (2): 105–116. doi:10.1080/00033796600203075. ISSN 0003-3790.
- The Nautical Almanac and Astronomical Ephemeris, for the year 1767
- "The History of HM Nautical Almanac Office". HM Nautical Almanac Office. Archived from the original on June 30, 2007. Retrieved July 31, 2007.
- "Nautical Almanac History". US Naval Observatory. Archived from the original on April 5, 2007. Retrieved July 31, 2007.
- Bronowski, Jacob (1990) [1973]. The Ascent of Man. London: BBC Books. p. 243. ISBN 978-0-563-20900-3.
- Fauque, Danielle M. E. (2015). "Testing Longitude Methods in Mid-Eighteenth Century France". In Dunn, Richard; Higgitt, Rebekah (eds.). Navigational Enterprises in Europe and its Empires, 1730–1850. London: Palgrave Macmillan UK. pp. 159–179. doi:10.1057/9781137520647_9. ISBN 978-1-349-56744-7.
- Wess, Jane (2015). "Navigation and Mathematics: A Match Made in the Heavens?". In Dunn, Richard; Higgitt, Rebekah (eds.). Navigational Enterprises in Europe and its Empires, 1730–1850. London: Palgrave Macmillan UK. pp. 201–222. doi:10.1057/9781137520647_11. ISBN 978-1-349-56744-7.
- Bown, Stephen R. (2001). "The astonishing astronomer of the great northwest". Mercator's World. 6 (2): 42.
- Sebert, L.M. (1971). The Determination of Longitude in Western Canada. Technical Report No: 71-3. Ottawa: Surveys and Mapping Branch, Department of Energy, Mines and Resources. Sebert gives 102° 16' as the longitude of Cumberland House, but Old Cumberland House, still in use at that time, was 2km to the east, see: "Cumberland House Provincial Park". Canada's Historic Places. Parks Canada. Retrieved August 21, 2020.
- de Mendoza Rios, Joseph (1805). A complete Collection of Tables for Navigation and nautical Astronomy. T Bensley.
- Wales, William (1794). The Method of Finding the Longitude at Sea, By Time-keepers. London: C. Buckton.
- Britten, Frederick James (1894). Former Clock & Watchmakers and Their Work. London: E. & F.N. Spon. pp. 271–274.
- Ritchie, G.S. (1967). The Admiralty Chart. London: Hollis & Carter. pp. 76–79.
- Brooks, Frederick J. (1995) [1975]. The Mythical Man-Month. Addison-Wesley. p. 64. ISBN 0-201-83595-9.
- R. Fitzroy. "Volume II: Proceedings of the Second Expedition". p. 18.
- Littlehales, G.W. (1909). "The Decline of the Lunar Distance for the Determination of the Time and Longitude at". Bulletin of the American Geographical Society. 41 (2): 83–86. doi:10.2307/200792. JSTOR 200792.
- Paine, Robert Treat; Borden, Simeon (1846). "Account of a Trigonometrical Survey of Massachusetts, by Simeon Borden, Esq., with a Comparison of Its Results with Those Obtained from Astronomical Observations, by Robert Treat Paine, Esq., Communicated by Mr. Borden". Transactions of the American Philosophical Society. 9 (1): 33–91. doi:10.2307/1005341. JSTOR 1005341.
- Gould, Benjamin Apthorp (1869). The Transatlantic Longitude, as Determined by the Coast Survey Expedition in 1866: A Report to the Superintendent of the US Coast Survey. Washington, D.C.: Smithsonian Institution.
- Walker, Sears C (1850). "Report on the experience of the Coast Survey in regard to telegraph operations, for determination of longitude &c". American Journal of Science and Arts. 10 (28): 151–160.
- Briggs, Charles Frederick; Maverick, Augustus (1858). The Story of the Telegraph, and a History of the Great Atlantic Cable: A Complete Record of the Inception, Progress, and Final Success of that Undertaking: a General History of Land and Oceanic Telegraphs: Descriptions of Telegraphic Apparatus, and Biographical Sketches of the Principal Persons Connected with the Great Work. New York: Rudd & Carleton.
- Schott, Charles A. (1897). "The telegraphic longitude net of the United States and its connection with that of Europe, as developed by the Coast and Geodetic Survey between 1866 and 1896". The Astronomical Journal. 18: 25–28. Bibcode:1897AJ.....18...25S. doi:10.1086/102749.
- Loomis, Elias (1856). The recent progress of astronomy, especially in the United States. Third Edition. New York: Harper and Brothers.
- Stachurski, Richard (2009). Longitude by Wire: Finding North America. Columbia: University of South Carolina Press. ISBN 978-1-57003-801-3.
- Ashe, E.D. (1860). "Longitudes of some of the principal places in Canada by electric telegraph". The Nautical Magazine. 29: 1–11.
- Jarrell, Richard (1988). The Cold Light of Dawn. A History of Canadian Astronomy. University of Toronto Press. pp. 37–39. doi:10.3138/9781487599935-004. ISBN 9781487599935.
- "The Telegraphic Longitude Net of the United States". Publications of the Astronomical Society of the Pacific. 9 (59): 242–244. 1897. JSTOR 40671094.
- Nelles, Douglas H. (1913). "The Exploration and Survey of the 141st Meridian, Alaska". The Geographical Journal. 41 (1): 48–56. doi:10.2307/1778488. JSTOR 1778488. Note: the author's name is incorrectly given as Nellas on the article, but correcty as Nelles on the map.
- Nesham, E.W. (1927). "The Alaska Boundary Demarcation". The Geographical Journal. 69 (1): 49–59. doi:10.2307/1782859. JSTOR 1782859.
- Bowie, William (1913). Astronomy: Determination of Time, Longitude, Latitude, and Azimuth, Volume 4 (5 ed.). U.S. Government Printing Office. pp. 78–102.
- Davis, Chales Henry; Norris, John Alexander (1885). Telegraphic Determination of Longitudes in Mexico and Central America and on the West Coast of South America: Embracing the Meridians of Vera Cruz; Guatemala; La Libertad; Salvador; Paita; Lima; Arica; Valparaiso; and the Argentine National Observatory at Cordoba; with the Latitudes of the Several Sea-coast Stations. Washington: US Hydrographic Office.
- Green, Francis Matthews (1877). Report on the telegraphic determination of differences of longitude in the West Indies and Central America. Washington: US Hydrographic Office.
- Green, Francis Matthews (1880). Telegraphic determination of longitudes on the east coast of South America embracing the meridians of Lisbon, Madeira, St. Vincent, Pernambuco, Bahia, Rio de Janeiro, Montevideo, Buenos Ayres, and Para, with the latitude of the several stations. Washington: US Hydrographic Office.
- Norris, John Alexander; Laird, Charles; Holcombe, John H.L.; Garrett, Le Roy M. (1891). Telegraphic determination of longitudes in Mexico, Central America, the West Indies, and on the north coast of South America, embracing the meridians of Coatzacoalcos; Salina Cruz; La Libertad; San Juan del Sur; St. Nicolas Mole; Port Plata; Santo Domingo; Curacao; and La Guayra, with the latitudes of the several stations. Washington: US Hydrographic Office.
- Airy, George Biddell (1881). Account of observations of the transit of Venus, 1874, December 8 : made under the authority of the British government : and of the reduction of the observations. London: Her Majesty's Stationery Office. pp. 257–346.
- Strahan, C. (1902). "The Survey of India". Professional Papers of the Corps of Royal Engineers. 28: 141–171.
- Walker, J.T. (1878). General Report on the Operations of the Great Trigonometrical Survey of India During 1876–77. Calcutta: Office of the Superintendent of Government Printing.
- Green, Francis Mathews; Davis, Charles Henry; Norris, John Alexander (1883). Telegraphic Determination of Longitudes in Japan, China, and the East Indies: Embracing the Meridians of Yokohama, Nagasaki, Wladiwostok, Shanghai, Amoy, Hong-Kong, Manila, Cape St. James, Singapore, Batavia, and Madras, with the Latitude of the Several Stations. Washington: US Hydrographic Office.
- Stewart, R.Meldrum (1924). "Dr. Otto Klotz". Journal of the Royal Astronomical Society of Canada. 18: 1–8. Bibcode:1924JRASC..18....1S.
- Kershaw, Michael (2014). "'A thorn in the side of European geodesy': measuring Paris–Greenwich longitude by electric telegraph". The British Journal for the History of Science. 47 (4): 637–660. doi:10.1017/S0007087413000988. ISSN 0007-0874. JSTOR 43820533. PMID 25546999.
- Fahie, John Joseph (1899). A History of Wireless Telegraphy, 1838–1899: Including Some Bare-wire Proposals for Subaqueous Telegraphs. Edinburgh and London: Willaim Blackwood and Sons. pp. 296–320.
- Munro, John (1902). "Time-Signals by Wireless Telegraphy". Nature. 66 (1713): 416. Bibcode:1902Natur..66..416M. doi:10.1038/066416d0. ISSN 0028-0836. S2CID 4021629.
- Cited in: Baracchi, P. (1914). Hall, T.S. (ed.). Australian Longitudes. Fourteenth Meeting of the Australian Association for the Advancement of Science, Melbourne, 1913. pp. 48–58. See page 56
- Cowie, George D.; Eckhardt, Engelhardt August (1924). Wireless longitude. Washington: US Government Printing Office. p. 1.
- Hutchinson, D.L. (1908). "Wireless Time Signals from the St. John Observatory of the Canadian Meteorological Service". Proceedings and Transactions of the Royal Society of Canada. Ser. 3 Vol. 2: 153–154.
- Lockyer, William J. S. (1913). "International Time and Weather Radio-Telegraphic Signals". Nature. 91 (2263): 33–36. Bibcode:1913Natur..91...33L. doi:10.1038/091033b0. ISSN 0028-0836. S2CID 3977506.
- Zimmerman, Arthur E. "The first wireless time signals to ships at sea" (PDF). antiquewireless.org. Antique Wireless Association. Retrieved July 9, 2020.
- Lombardi, Michael A., "Radio Controlled Clocks" (PDF). Archived from the original (PDF) on February 7, 2012. Retrieved October 30, 2007. (983 KB), Proceedings of the 2003 National Conference of Standards Laboratories International, August 17, 2003
- Boulnois, P.K.; Aston, C.J. (1924). "Field-Longitudes by Wireless". The Geographical Journal. 63 (4): 318–331. doi:10.2307/1781410. JSTOR 1781410.
- Pierce, J.A. (1946). "An introduction to Loran". Proceedings of the IRE. 34 (5): 216–234. doi:10.1109/JRPROC.1946.234564. S2CID 20739091.
- Tesla, Nicolas (1908). "The Future Of The Wireless Art". In Massie, Walter W.; Underhill, Charles R. (eds.). Wireless Telegraphy & Telephony. Van Norstrand. pp. 67–71.

.jpg.webp)

.png.webp)