Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre (1834–1886), are nontrivial solutions of Laguerre's differential equation:
_with_n_as_-1_divided_by_9_and_x_as_z_to_the_power_of_4_from_-2-2i_to_2%252B2i.svg.png.webp)
which is a second-order linear differential equation. This equation has nonsingular solutions only if n is a non-negative integer.
Sometimes the name Laguerre polynomials is used for solutions of
where n is still a non-negative integer. Then they are also named generalized Laguerre polynomials, as will be done here (alternatively associated Laguerre polynomials or, rarely, Sonine polynomials, after their inventor[1] Nikolay Yakovlevich Sonin).
More generally, a Laguerre function is a solution when n is not necessarily a non-negative integer.
The Laguerre polynomials are also used for Gauss–Laguerre quadrature to numerically compute integrals of the form
These polynomials, usually denoted L0, L1, …, are a polynomial sequence which may be defined by the Rodrigues formula,
reducing to the closed form of a following section.
They are orthogonal polynomials with respect to an inner product
The rook polynomials in combinatorics are more or less the same as Laguerre polynomials, up to elementary changes of variables. Further see the Tricomi–Carlitz polynomials.
The Laguerre polynomials arise in quantum mechanics, in the radial part of the solution of the Schrödinger equation for a one-electron atom. They also describe the static Wigner functions of oscillator systems in quantum mechanics in phase space. They further enter in the quantum mechanics of the Morse potential and of the 3D isotropic harmonic oscillator.
Physicists sometimes use a definition for the Laguerre polynomials that is larger by a factor of n! than the definition used here. (Likewise, some physicists may use somewhat different definitions of the so-called associated Laguerre polynomials.)
The first few polynomials
These are the first few Laguerre polynomials:
| n | |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| n |
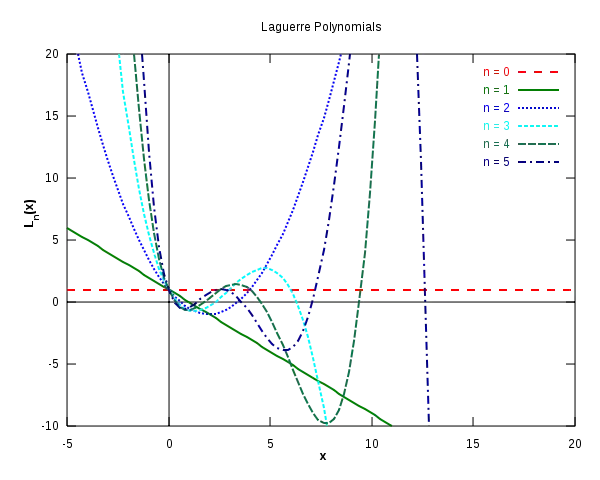
Recursive definition, closed form, and generating function
One can also define the Laguerre polynomials recursively, defining the first two polynomials as
and then using the following recurrence relation for any k ≥ 1:
Furthermore,
In solution of some boundary value problems, the characteristic values can be useful:
The closed form is
The generating function for them likewise follows,
Polynomials of negative index can be expressed using the ones with positive index:
Generalized Laguerre polynomials
For arbitrary real α the polynomial solutions of the differential equation[2]
are called generalized Laguerre polynomials, or associated Laguerre polynomials.
One can also define the generalized Laguerre polynomials recursively, defining the first two polynomials as
and then using the following recurrence relation for any k ≥ 1:
The simple Laguerre polynomials are the special case α = 0 of the generalized Laguerre polynomials:
The Rodrigues formula for them is
The generating function for them is
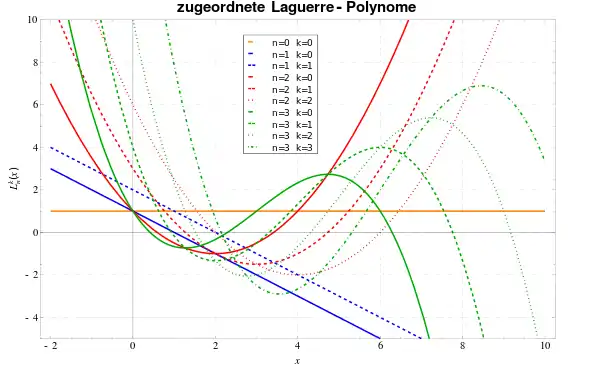
Explicit examples and properties of the generalized Laguerre polynomials
- Laguerre functions are defined by confluent hypergeometric functions and Kummer's transformation as[3] where is a generalized binomial coefficient. When n is an integer the function reduces to a polynomial of degree n. It has the alternative expression[4]in terms of Kummer's function of the second kind.
- The closed form for these generalized Laguerre polynomials of degree n is[5] derived by applying Leibniz's theorem for differentiation of a product to Rodrigues' formula.
- Laguerre polynomials have a differential operator representation, much like the closely related Hermite polynomials. Namely, let and consider the differential operator . Then .
- The first few generalized Laguerre polynomials are:
- The coefficient of the leading term is (−1)n/n!;
- The constant term, which is the value at 0, is
- If α is non-negative, then Ln(α) has n real, strictly positive roots (notice that is a Sturm chain), which are all in the interval
- The polynomials' asymptotic behaviour for large n, but fixed α and x > 0, is given by[6][7] and summarizing bywhere is the Bessel function.
As a contour integral
Given the generating function specified above, the polynomials may be expressed in terms of a contour integral
where the contour circles the origin once in a counterclockwise direction without enclosing the essential singularity at 1
Recurrence relations
The addition formula for Laguerre polynomials:[8]
Laguerre's polynomials satisfy the recurrence relations
in particular
and
or
moreover
They can be used to derive the four 3-point-rules
combined they give this additional, useful recurrence relations
Since is a monic polynomial of degree in , there is the partial fraction decomposition
The second equality follows by the following identity, valid for integer i and n and immediate from the expression of in terms of Charlier polynomials:
For the third equality apply the fourth and fifth identities of this section.
Derivatives of generalized Laguerre polynomials
Differentiating the power series representation of a generalized Laguerre polynomial k times leads to
This points to a special case (α = 0) of the formula above: for integer α = k the generalized polynomial may be written
the shift by k sometimes causing confusion with the usual parenthesis notation for a derivative.
Moreover, the following equation holds:
which generalizes with Cauchy's formula to
The derivative with respect to the second variable α has the form,[9]
This is evident from the contour integral representation below.
The generalized Laguerre polynomials obey the differential equation
which may be compared with the equation obeyed by the kth derivative of the ordinary Laguerre polynomial,
where for this equation only.
In Sturm–Liouville form the differential equation is
which shows that L(α)
n is an eigenvector for the eigenvalue n.
Orthogonality
The generalized Laguerre polynomials are orthogonal over [0, ∞) with respect to the measure with weighting function xα e−x:[10]
which follows from
If denotes the gamma distribution then the orthogonality relation can be written as
The associated, symmetric kernel polynomial has the representations (Christoffel–Darboux formula)
recursively
Moreover,
Turán's inequalities can be derived here, which is
The following integral is needed in the quantum mechanical treatment of the hydrogen atom,
Series expansions
Let a function have the (formal) series expansion
Then
The series converges in the associated Hilbert space L2[0, ∞) if and only if
Further examples of expansions
Monomials are represented as
while binomials have the parametrization
This leads directly to
for the exponential function. The incomplete gamma function has the representation
In quantum mechanics
In quantum mechanics the Schrödinger equation for the hydrogen-like atom is exactly solvable by separation of variables in spherical coordinates. The radial part of the wave function is a (generalized) Laguerre polynomial.[11]
Vibronic transitions in the Franck-Condon approximation can also be described using Laguerre polynomials.[12]
Relation to Hermite polynomials
The generalized Laguerre polynomials are related to the Hermite polynomials:
where the Hn(x) are the Hermite polynomials based on the weighting function exp(−x2), the so-called "physicist's version."
Because of this, the generalized Laguerre polynomials arise in the treatment of the quantum harmonic oscillator.
Relation to hypergeometric functions
The Laguerre polynomials may be defined in terms of hypergeometric functions, specifically the confluent hypergeometric functions, as
where is the Pochhammer symbol (which in this case represents the rising factorial).
Hardy–Hille formula
The generalized Laguerre polynomials satisfy the Hardy–Hille formula[14][15]
where the series on the left converges for and . Using the identity
(see generalized hypergeometric function), this can also be written as
This formula is a generalization of the Mehler kernel for Hermite polynomials, which can be recovered from it by using the relations between Laguerre and Hermite polynomials given above.
Physicist Scaling Convention
The generalized Laguerre polynomials are used to describe the quantum wavefunction for hydrogen atom orbitals. In the introductory literature on this topic,[16][17][18] a different scaling is used for the generalized Laguerre polynomials than the scaling presented in this article. In the convention taken here, the generalized Laguerre polynomials can be expressed as [19]
where is the confluent hypergeometric function. In the physicist literature, such as [18], the generalized Laguerre polynomials are instead defined as
The physicist version is related to the standard version by
There is yet another convention in use, though less frequently, in the physics literature. Under this convention the Laguerre polynomials are given by [20][21][22]
Umbral Calculus Convention
Generalized Laguerre polynomials are linked to Umbral calculus by being Sheffer sequences for when multiplied by . In Umbral Calculus convention,[23] the default Laguerre polynomials are defined to be
where are the signless Lah numbers. is a sequence of polynomials of binomial type, ie they satisfy
See also
- Orthogonal polynomials
- Rodrigues' formula
- Angelescu polynomials
- Bessel polynomials
- Denisyuk polynomials
- Transverse mode, an important application of Laguerre polynomials to describe the field intensity within a waveguide or laser beam profile.
Notes
- N. Sonine (1880). "Recherches sur les fonctions cylindriques et le développement des fonctions continues en séries". Math. Ann. 16 (1): 1–80. doi:10.1007/BF01459227. S2CID 121602983.
- A&S p. 781
- A&S p. 509
- A&S p. 510
- A&S p. 775
- Szegő, p. 198.
- D. Borwein, J. M. Borwein, R. E. Crandall, "Effective Laguerre asymptotics", SIAM J. Numer. Anal., vol. 46 (2008), no. 6, pp. 3285–3312 doi:10.1137/07068031X
- A&S equation (22.12.6), p. 785
- Koepf, Wolfram (1997). "Identities for families of orthogonal polynomials and special functions". Integral Transforms and Special Functions. 5 (1–2): 69–102. CiteSeerX 10.1.1.298.7657. doi:10.1080/10652469708819127.
- "Associated Laguerre Polynomial".
- Ratner, Schatz, Mark A., George C. (2001). Quantum Mechanics in Chemistry. 0-13-895491-7: Prentice Hall. pp. 90–91.
{{cite book}}: CS1 maint: location (link) CS1 maint: multiple names: authors list (link) - Jong, Mathijs de; Seijo, Luis; Meijerink, Andries; Rabouw, Freddy T. (2015-06-24). "Resolving the ambiguity in the relation between Stokes shift and Huang–Rhys parameter". Physical Chemistry Chemical Physics. 17 (26): 16959–16969. Bibcode:2015PCCP...1716959D. doi:10.1039/C5CP02093J. hdl:1874/321453. ISSN 1463-9084. PMID 26062123. S2CID 34490576.
- C. Truesdell, "On the Addition and Multiplication Theorems for the Special Functions", Proceedings of the National Academy of Sciences, Mathematics, (1950) pp. 752–757.
- Szegő, p. 102.
- W. A. Al-Salam (1964), "Operational representations for Laguerre and other polynomials", Duke Math J. 31 (1): 127–142.
- Griffiths, David J. (2005). Introduction to quantum mechanics (2nd ed.). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 0131118927.
- Sakurai, J. J. (2011). Modern quantum mechanics (2nd ed.). Boston: Addison-Wesley. ISBN 978-0805382914.
- Merzbacher, Eugen (1998). Quantum mechanics (3rd ed.). New York: Wiley. ISBN 0471887021.
- Abramowitz, Milton (1965). Handbook of mathematical functions, with formulas, graphs, and mathematical tables. New York: Dover Publications. ISBN 978-0-486-61272-0.
- Schiff, Leonard I. (1968). Quantum mechanics (3d ed.). New York: McGraw-Hill. ISBN 0070856435.
- Messiah, Albert (2014). Quantum Mechanics. Dover Publications. ISBN 9780486784557.
- Boas, Mary L. (2006). Mathematical methods in the physical sciences (3rd ed.). Hoboken, NJ: Wiley. ISBN 9780471198260.
- Rota, Gian-Carlo; Kahaner, D; Odlyzko, A (1973-06-01). "On the foundations of combinatorial theory. VIII. Finite operator calculus". Journal of Mathematical Analysis and Applications. 42 (3): 684–760. doi:10.1016/0022-247X(73)90172-8. ISSN 0022-247X.
References
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- G. Szegő, Orthogonal polynomials, 4th edition, Amer. Math. Soc. Colloq. Publ., vol. 23, Amer. Math. Soc., Providence, RI, 1975.
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- B. Spain, M.G. Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 10 deals with Laguerre polynomials.
- "Laguerre polynomials", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Eric W. Weisstein, "Laguerre Polynomial", From MathWorld—A Wolfram Web Resource.
- George Arfken and Hans Weber (2000). Mathematical Methods for Physicists. Academic Press. ISBN 978-0-12-059825-0.