Kolmogorov structure function
In 1973, Andrey Kolmogorov proposed a non-probabilistic approach to statistics and model selection. Let each datum be a finite binary string and a model be a finite set of binary strings. Consider model classes consisting of models of given maximal Kolmogorov complexity. The Kolmogorov structure function of an individual data string expresses the relation between the complexity level constraint on a model class and the least log-cardinality of a model in the class containing the data. The structure function determines all stochastic properties of the individual data string: for every constrained model class it determines the individual best-fitting model in the class irrespective of whether the true model is in the model class considered or not. In the classical case we talk about a set of data with a probability distribution, and the properties are those of the expectations. In contrast, here we deal with individual data strings and the properties of the individual string focused on. In this setting, a property holds with certainty rather than with high probability as in the classical case. The Kolmogorov structure function precisely quantifies the goodness-of-fit of an individual model with respect to individual data.
The Kolmogorov structure function is used in the algorithmic information theory, also known as the theory of Kolmogorov complexity, for describing the structure of a string by use of models of increasing complexity.
Kolmogorov's definition

The structure function was originally proposed by Kolmogorov in 1973 at a Soviet Information Theory symposium in Tallinn, but these results were not published[1] p. 182. But the results were announced in[2] in 1974, the only written record by Kolmogorov himself. One of his last scientific statements is (translated from the original Russian by L.A. Levin):
To each constructive object corresponds a function of a natural number k—the log of minimal cardinality of x-containing sets that allow definitions of complexity at most k. If the element x itself allows a simple definition, then the function drops to 0 even for small k. Lacking such definition, the element is "random" in a negative sense. But it is positively "probabilistically random" only when function having taken the value at a relatively small , then changes approximately as .
— Kolmogorov, announcement cited above
Contemporary definition
It is discussed in Cover and Thomas.[1] It is extensively studied in Vereshchagin and Vitányi[3] where also the main properties are resolved. The Kolmogorov structure function can be written as
where is a binary string of length with where is a contemplated model (set of n-length strings) for , is the Kolmogorov complexity of and is a nonnegative integer value bounding the complexity of the contemplated 's. Clearly, this function is nonincreasing and reaches for where is the required number of bits to change into and is the Kolmogorov complexity of .
The algorithmic sufficient statistic
We define a set containing such that
- .
The function never decreases more than a fixed independent constant below the diagonal called sufficiency line L defined by
- .
It is approached to within a constant distance by the graph of for certain arguments (for instance, for ). For these 's we have and the associated model (witness for ) is called an optimal set for , and its description of bits is therefore an algorithmic sufficient statistic. We write `algorithmic' for `Kolmogorov complexity' by convention. The main properties of an algorithmic sufficient statistic are the following: If is an algorithmic sufficient statistic for , then
- .
That is, the two-part description of using the model and as data-to-model code the index of in the enumeration of in bits, is as concise as the shortest one-part code of in bits. This can be easily seen as follows:
- ,
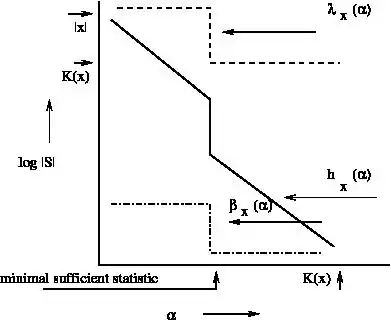
using straightforward inequalities and the sufficiency property, we find that . (For example, given , we can describe self-delimitingly (you can determine its end) in bits.) Therefore, the randomness deficiency of in is a constant, which means that is a typical (random) element of S. However, there can be models containing that are not sufficient statistics. An algorithmic sufficient statistic for has the additional property, apart from being a model of best fit, that and therefore by the Kolmogorov complexity symmetry of information (the information about in is about the same as the information about in x) we have : the algorithmic sufficient statistic is a model of best fit that is almost completely determined by . ( is a shortest program for .) The algorithmic sufficient statistic associated with the least such is called the algorithmic minimal sufficient statistic.
With respect to the picture: The MDL structure function is explained below. The Goodness-of-fit structure function is the least randomness deficiency (see above) of any model for such that . This structure function gives the goodness-of-fit of a model (containing x) for the string x. When it is low the model fits well, and when it is high the model doesn't fit well. If for some then there is a typical model for such that and is typical (random) for S. That is, is the best-fitting model for x. For more details see[1] and especially[3] and.[4]
Selection of properties
Within the constraints that the graph goes down at an angle of at least 45 degrees, that it starts at n and ends approximately at , every graph (up to a additive term in argument and value) is realized by the structure function of some data x and vice versa. Where the graph hits the diagonal first the argument (complexity) is that of the minimum sufficient statistic. It is incomputable to determine this place. See.[3]
Main property
It is proved that at each level of complexity the structure function allows us to select the best model for the individual string x within a strip of with certainty, not with great probability.[3]
The MDL variant
The Minimum description length (MDL) function: The length of the minimal two-part code for x consisting of the model cost K(S) and the length of the index of x in S, in the model class of sets of given maximal Kolmogorov complexity , the complexity of S upper bounded by , is given by the MDL function or constrained MDL estimator:
where is the total length of two-part code of x with help of model S.
Main property
It is proved that at each level of complexity the structure function allows us to select the best model S for the individual string x within a strip of with certainty, not with great probability.[3]
Application in statistics
The mathematics developed above were taken as the foundation of MDL by its inventor Jorma Rissanen.[5]
Probability models
For every computable probability distribution it can be proved[6] that
- .
For example, if is some computable distribution on the set of strings of length , then each has probability . Kolmogorov's structure function becomes
where x is a binary string of length n with where is a contemplated model (computable probability of -length strings) for , is the Kolmogorov complexity of and is an integer value bounding the complexity of the contemplated 's. Clearly, this function is non-increasing and reaches for where c is the required number of bits to change into and is the Kolmogorov complexity of . Then . For every complexity level the function is the Kolmogorov complexity version of the maximum likelihood (ML).
Main property
It is proved that at each level of complexity the structure function allows us to select the best model for the individual string within a strip of with certainty, not with great probability.[3]
The MDL variant and probability models
The MDL function: The length of the minimal two-part code for x consisting of the model cost K(P) and the length of , in the model class of computable probability mass functions of given maximal Kolmogorov complexity , the complexity of P upper bounded by , is given by the MDL function or constrained MDL estimator:
where is the total length of two-part code of x with help of model P.
Main property
It is proved that at each level of complexity the MDL function allows us to select the best model P for the individual string x within a strip of with certainty, not with great probability.[3]
Extension to rate distortion and denoising
It turns out that the approach can be extended to a theory of rate distortion of individual finite sequences and denoising of individual finite sequences[7] using Kolmogorov complexity. Experiments using real compressor programs have been carried out with success.[8] Here the assumption is that for natural data the Kolmogorov complexity is not far from the length of a compressed version using a good compressor.
References
- Cover, Thomas M.; Thomas, Joy A. (1991). Elements of information theory. New York: Wiley. pp. 175–178. ISBN 978-0471062592.
- Abstract of a talk for the Moscow Mathematical Society in Uspekhi Mat. Nauk Volume 29, Issue 4(178) in the Communications of the Moscow Mathematical Society page 155 (in the Russian edition, not translated into English)
- Vereshchagin, N.K.; Vitanyi, P.M.B. (1 December 2004). "Kolmogorov's Structure Functions and Model Selection". IEEE Transactions on Information Theory. 50 (12): 3265–3290. arXiv:cs/0204037. doi:10.1109/TIT.2004.838346.
- Gacs, P.; Tromp, J.T.; Vitanyi, P.M.B. (2001). "Algorithmic statistics". IEEE Transactions on Information Theory. 47 (6): 2443–2463. arXiv:math/0006233. doi:10.1109/18.945257.
- Rissanen, Jorma (2007). Information and complexity in statistical modeling (Online-Ausg. ed.). New York: Springer. ISBN 978-0-387-36610-4.
- A.Kh. Shen, The concept of (α, β)-stochasticity in the Kolmogorov sense, and its properties, Soviet Math. Dokl., 28:1(1983), 295--299
- Vereshchagin, Nikolai K.; Vitanyi, Paul M.B. (1 July 2010). "Rate Distortion and Denoising of Individual Data Using Kolmogorov Complexity". IEEE Transactions on Information Theory. 56 (7): 3438–3454. arXiv:cs/0411014. doi:10.1109/TIT.2010.2048491.
- de Rooij, Steven; Vitanyi, Paul (1 March 2012). "Approximating Rate-Distortion Graphs of Individual Data: Experiments in Lossy Compression and Denoising". IEEE Transactions on Computers. 61 (3): 395–407. arXiv:cs/0609121. doi:10.1109/TC.2011.25.
Literature
- Cover, T.M.; P. Gacs; R.M. Gray (1989). "Kolmogorov's contributions to Information Theory and Algorithmic Complexity". Annals of Probability. 17 (3): 840–865. doi:10.1214/aop/1176991250. JSTOR 2244387.
- Kolmogorov, A. N.; Uspenskii, V. A. (1 January 1987). "Algorithms and Randomness". Theory of Probability and Its Applications. 32 (3): 389–412. doi:10.1137/1132060.
- Li, M., Vitányi, P.M.B. (2008). An introduction to Kolmogorov complexity and its applications (3rd ed.). New York: Springer. ISBN 978-0387339986.
{{cite book}}: CS1 maint: multiple names: authors list (link), Especially pp. 401–431 about the Kolmogorov structure function, and pp. 613–629 about rate distortion and denoising of individual sequences. - Shen, A. (1 April 1999). "Discussion on Kolmogorov Complexity and Statistical Analysis". The Computer Journal. 42 (4): 340–342. doi:10.1093/comjnl/42.4.340.
- V'yugin, V.V. (1987). "On Randomness Defect of a Finite Object Relative to Measures with Given Complexity Bounds". Theory of Probability and Its Applications. 32 (3): 508–512. doi:10.1137/1132071.
- V'yugin, V. V. (1 April 1999). "Algorithmic Complexity and Stochastic Properties of Finite Binary Sequences". The Computer Journal. 42 (4): 294–317. doi:10.1093/comjnl/42.4.294.