Jacobi's theorem (geometry)
In plane geometry, a Jacobi point is a point in the Euclidean plane determined by a triangle △ABC and a triple of angles α, β, γ. This information is sufficient to determine three points X, Y, Z such that
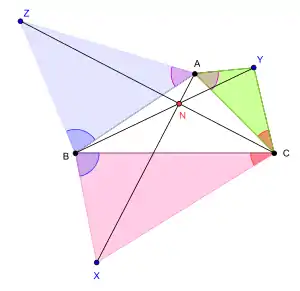
Adjacent colored angles are equal in measure. The point N is the Jacobi point for triangle △ABC and these angles.
Then, by a theorem of Karl Friedrich Andreas Jacobi, the lines AX, BY, CZ are concurrent,[1][2][3] at a point N called the Jacobi point.[3]
The Jacobi point is a generalization of the Fermat point, which is obtained by letting α = β = γ = 60° and △ABC having no angle being greater or equal to 120°.
If the three angles above are equal, then N lies on the rectangular hyperbola given in areal coordinates by
which is Kiepert's hyperbola. Each choice of three equal angles determines a triangle center.
References
- de Villiers, Michael (2009). Some Adventures in Euclidean Geometry. Dynamic Mathematics Learning. pp. 138–140. ISBN 9780557102952.
- Glenn T. Vickers, "Reciprocal Jacobi Triangles and the McCay Cubic", Forum Geometricorum 15, 2015, 179–183. http://forumgeom.fau.edu/FG2015volume15/FG201518.pdf
- Glenn T. Vickers, "The 19 Congruent Jacobi Triangles", Forum Geometricorum 16, 2016, 339–344. http://forumgeom.fau.edu/FG2016volume16/FG201642.pdf
Weblinks
- A simple proof of Jacobi's theorem written by Kostas Vittas
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.