Intersymbol interference
In telecommunication, intersymbol interference (ISI) is a form of distortion of a signal in which one symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have a similar effect as noise, thus making the communication less reliable. The spreading of the pulse beyond its allotted time interval causes it to interfere with neighboring pulses.[1] ISI is usually caused by multipath propagation or the inherent linear or non-linear frequency response of a communication channel causing successive symbols to blur together.
The presence of ISI in the system introduces errors in the decision device at the receiver output. Therefore, in the design of the transmitting and receiving filters, the objective is to minimize the effects of ISI, and thereby deliver the digital data to its destination with the smallest error rate possible.
Ways to alleviate intersymbol interference include adaptive equalization and error correcting codes.[2]
Causes
Multipath propagation
One of the causes of intersymbol interference is multipath propagation in which a wireless signal from a transmitter reaches the receiver via multiple paths. The causes of this include reflection (for instance, the signal may bounce off buildings), refraction (such as through the foliage of a tree) and atmospheric effects such as atmospheric ducting and ionospheric reflection. Since the various paths can be of different lengths, this results in the different versions of the signal arriving at the receiver at different times. These delays mean that part or all of a given symbol will be spread into the subsequent symbols, thereby interfering with the correct detection of those symbols. Additionally, the various paths often distort the amplitude and/or phase of the signal, thereby causing further interference with the received signal.
Bandlimited channels
Another cause of intersymbol interference is the transmission of a signal through a bandlimited channel, i.e., one where the frequency response is zero above a certain frequency (the cutoff frequency). Passing a signal through such a channel results in the removal of frequency components above this cutoff frequency. In addition, components of the frequency below the cutoff frequency may also be attenuated by the channel.
This filtering of the transmitted signal affects the shape of the pulse that arrives at the receiver. The effects of filtering a rectangular pulse not only change the shape of the pulse within the first symbol period, but it is also spread out over the subsequent symbol periods. When a message is transmitted through such a channel, the spread pulse of each individual symbol will interfere with following symbols.
Bandlimited channels are present in both wired and wireless communications. The limitation is often imposed by the desire to operate multiple independent signals through the same area/cable; due to this, each system is typically allocated a piece of the total bandwidth available. For wireless systems, they may be allocated a slice of the electromagnetic spectrum to transmit in (for example, FM radio is often broadcast in the 87.5–108 MHz range). This allocation is usually administered by a government agency; in the case of the United States this is the Federal Communications Commission (FCC). In a wired system, such as an optical fiber cable, the allocation will be decided by the owner of the cable.
The bandlimiting can also be due to the physical properties of the medium - for instance, the cable being used in a wired system may have a cutoff frequency above which practically none of the transmitted signal will propagate.
Communication systems that transmit data over bandlimited channels usually implement pulse shaping to avoid interference caused by the bandwidth limitation. If the channel frequency response is flat and the shaping filter has a finite bandwidth, it is possible to communicate with no ISI at all. Often the channel response is not known beforehand, and an adaptive equalizer is used to compensate the frequency response.
Effects on eye patterns
One way to study ISI in a PCM or data transmission system experimentally is to apply the received wave to the vertical deflection plates of an oscilloscope and to apply a sawtooth wave at the transmitted symbol rate R (R = 1/T) to the horizontal deflection plates. The resulting display is called an eye pattern because of its resemblance to the human eye for binary waves. The interior region of the eye pattern is called the eye opening. An eye pattern provides a great deal of information about the performance of the pertinent system.
- The width of the eye opening defines the time interval over which the received wave can be sampled without error from ISI. It is apparent that the preferred time for sampling is the instant of time at which the eye is open widest.
- The sensitivity of the system to timing error is determined by the rate of closure of the eye as the sampling time is varied.
- The height of the eye opening, at a specified sampling time, defines the margin over noise.
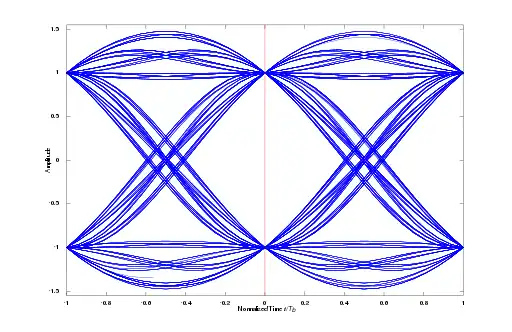The eye diagram of a binary PSK system
The eye diagram of the same system with multipath effects added
An eye pattern, which overlays many samples of a signal, can give a graphical representation of the signal characteristics. The first image above is the eye pattern for a binary phase-shift keying (PSK) system in which a one is represented by an amplitude of −1 and a zero by an amplitude of +1. The current sampling time is at the center of the image and the previous and next sampling times are at the edges of the image. The various transitions from one sampling time to another (such as one-to-zero, one-to-one and so forth) can clearly be seen on the diagram.
The noise margin - the amount of noise required to cause the receiver to get an error - is given by the distance between the signal and the zero amplitude point at the sampling time; in other words, the further from zero at the sampling time the signal is the better. For the signal to be correctly interpreted, it must be sampled somewhere between the two points where the zero-to-one and one-to-zero transitions cross. Again, the further apart these points are the better, as this means the signal will be less sensitive to errors in the timing of the samples at the receiver.
The effects of ISI are shown in the second image which is an eye pattern of the same system when operating over a multipath channel. The effects of receiving delayed and distorted versions of the signal can be seen in the loss of definition of the signal transitions. It also reduces both the noise margin and the window in which the signal can be sampled, which shows that the performance of the system will be worse (i.e. it will have a greater bit error ratio).
Countering ISI
There are several techniques in telecommunication and data storage that try to work around the problem of intersymbol interference.
- Design systems such that the impulse response is short enough that very little energy from one symbol smears into the next symbol.
- Separate symbols in time with guard periods.
- Apply an equalizer at the receiver, that, broadly speaking, attempts to undo the effect of the channel by applying an inverse filter.
- Apply a sequence detector at the receiver, that attempts to estimate the sequence of transmitted symbols using the Viterbi algorithm.
Intentional intersymbol interference
Coded modulation systems also exist that intentionally build a controlled amount of ISI into the system at the transmitter side, known as faster-than-Nyquist signaling. Such a design trades a computational complexity penalty at the receiver against a Shannon capacity gain of the overall transceiver system.[3]
See also
References
- Lathi, B.P.; Ding, Zhi (2009). Modern Digital and Analog Communication Systems (Fourth ed.). Oxford University Press, Inc. p. 95. ISBN 9780195331455.
- Digital Communications by Simon Haykin, McMaster University
- Faster than Nyquist Signaling, by J.B. Anderson, F. Rusek, and V. Owall, Proceedings of the IEEE, Aug. 2013
Further reading
- William J. Dally and John W. Poulton (1998). Digital Systems Engineering. Cambridge University Press. pp. 280–285. ISBN 9780521592925.
- Hervé Benoit (2002). Digital Television. Focal Press. pp. 90–91. ISBN 9780240516950.