Holditch's theorem
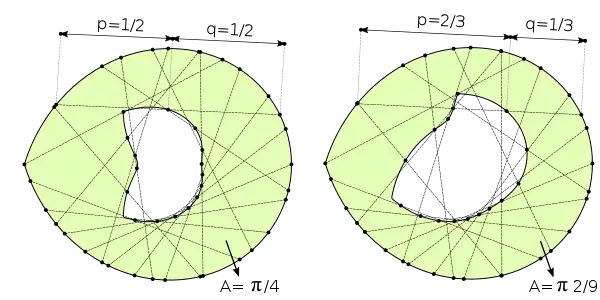
In plane geometry, Holditch's theorem states that if a chord of fixed length is allowed to rotate inside a convex closed curve, then the locus of a point on the chord a distance p from one end and a distance q from the other is a closed curve whose enclosed area is less than that of the original curve by . The theorem was published in 1858 by Rev. Hamnet Holditch.[1][2] While not mentioned by Holditch, the proof of the theorem requires an assumption that the chord be short enough that the traced locus is a simple closed curve.[3]
Observations
The theorem is included as one of Clifford Pickover's 250 milestones in the history of mathematics.[1] Some peculiarities of the theorem include that the area formula is independent of both the shape and the size of the original curve, and that the area formula is the same as for that of the area of an ellipse with semi-axes p and q. The theorem's author was a president of Caius College, Cambridge.
Extensions
Broman[3] gives a more precise statement of the theorem, along with a generalization. The generalization allows, for example, consideration of the case in which the outer curve is a triangle, so that the conditions of the precise statement of Holditch's theorem do not hold because the paths of the endpoints of the chord have retrograde portions (portions that retrace themselves) whenever an acute angle is traversed. Nevertheless, the generalization shows that if the chord is shorter than any of the triangle's altitudes, and is short enough that the traced locus is a simple curve, Holditch's formula for the in-between area is still correct (and remains so if the triangle is replaced by any convex polygon with a short enough chord). However, other cases result in different formulas.
References
- Pickover, Clifford (1 September 2009), "Holditch's Theorem", The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, Sterling, p. 250, ISBN 978-1-4027-5796-9
- Holditch, Rev. Hamnet (1858), "Geometrical theorem", The Quarterly Journal of Pure and Applied Mathematics, 2: 38
- Broman, Arne (1981), "Holditch's theorem: A fresh look at a long-forgotten theorem", Mathematics Magazine, 54 (3): 99–108, doi:10.2307/2689793, JSTOR 2689793, MR 0618595
Further reading
- B. Williamson, FRS, An elementary treatise on the integral calculus : containing applications to plane curves and surfaces, with numerous examples (Longmans, Green, London, 1875; 2nd 1877; 3rd 1880; 4th 1884; 5th 1888; 6th 1891; 7th 1896; 8th 1906; 1912, 1916, 1918, 1926); Ist 1875, pp. 192–193, with citation of Holditch's Prize Question set in The Lady's and Gentleman's Diary for 1857 (appearing in late 1856), with extension by Woolhouse in the issue for 1858; 5th 1888; 8th 1906 pp. 206–211
- J. Edwards, A Treatise on the Integral Calculus with Applications, Examples and Problems, Vol. 1 (Macmillan, London, 1921), Chap. XV, esp. Sections 478, 481–491, 496 (see also Chap. XIX for instantaneous centers, roulettes and glisettes); expounds and references extensions due to Woolhouse, Elliott, Leudesdorf, Kempe, drawing on the earlier book of Williamson.
- Kılıç, Erol; Keleş, Sadık (1994), "On Holditch's theorem and polar inertia momentum", Communications Faculty of Sciences University of Ankara, Series A1: Mathematics and Statistics, 43 (1–2): 41–47 (1996), MR 1404786
- Cooker, Mark J. (July 1998), "An extension of Holditch's theorem on the area within a closed curve", The Mathematical Gazette, 82 (494): 183–188, doi:10.2307/3620400, JSTOR 3620400, S2CID 123443685
- Cooker, Mark J. (March 1999), "On sweeping out an area", The Mathematical Gazette, 83 (496): 69–73, doi:10.2307/3618685, JSTOR 3618685, S2CID 125103358
- Apostol, Tom M.; Mnatsakanian, Mamikon A. (2012), "9.13 Remarks concerning Holditch's theorem", New Horizons in Geometry, The Dolciani Mathematical Expositions, vol. 47, Washington, DC: Mathematical Association of America, pp. 291–294, ISBN 978-0-88385-354-2, MR 3024916