Hendecagrammic prism

In geometry, a hendecagrammic prism is a star polyhedron made from two identical regular hendecagrams connected by squares. The related hendecagrammic antiprisms are made from two identical regular hendecagrams connected by equilateral triangles.

The four regular hendecagrams
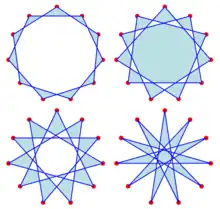
{11/2}, {11/3}, {11/4}, and {11/5}

Hendecagrammic prisms and bipyramids

There are 4 hendecagrammic uniform prisms, and 6 hendecagrammic uniform antiprisms. The prisms are constructed by 4.4.11/q vertex figures, Coxeter diagram. The hendecagrammic bipyramids, duals to the hendecagrammic prisms are also given.

Symmetry Prisms
D11h
[2,11]
(*2.2.11)
4.4.11/2
4.4.11/3
4.4.11/4
4.4.11/5
D11h
[2,11]
(*2.2.11)



Hendecagrammic antiprisms

The antiprisms with 3.3.3.3.11/q vertex figures, . Uniform antiprisms exist for p/q>3/2,[1] and are called crossed for p/q<2. For hendecagonal antiprism, two crossed antiprisms can not be constructed as uniform (with equilateral triangles): 11/8, and 11/9.

Symmetry Antiprisms Crossed- antiprisms
D11h
[2,11]
(*2.2.11)
3.3.3.11/2
 
3.3.3.11/4
 
3.3.3.11/6
3.3.3.-11/5
 Nonuniform
3.3.3.11/8
3.3.3.-11/3
D11d
[2+,11]
(2*11)
3.3.3.11/3
 
3.3.3.11/5
 
3.3.3.11/7
3.3.3.-11/4
 Nonuniform
3.3.3.11/9
3.3.3.-11/2

Hendecagrammic trapezohedra

The hendecagrammic trapezohedra are duals to the hendecagrammic antiprisms.

Symmetry Trapezohedra
D11h
[2,11]
(*2.2.11)


D11d
[2+,11]
(2*11)


See also

References
  1. Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.