Hammett equation

In organic chemistry, the Hammett equation describes a linear free-energy relationship relating reaction rates and equilibrium constants for many reactions involving benzoic acid derivatives with meta- and para-substituents to each other with just two parameters: a substituent constant and a reaction constant.[1][2] This equation was developed and published by Louis Plack Hammett in 1937[3] as a follow-up to qualitative observations in his 1935 publication.[4]

The basic idea is that for any two reactions with two aromatic reactants only differing in the type of substituent, the change in free energy of activation is proportional to the change in Gibbs free energy.[5] This notion does not follow from elemental thermochemistry or chemical kinetics and was introduced by Hammett intuitively.[lower-alpha 1]

The basic equation is:

\log {\frac {K}{K_{0}}}=\sigma \rho

where

{K}_{0}

= Reference constant

\sigma

= Substituent constant

\rho

= Reaction rate constant

relating the equilibrium constant, ${K}$ , for a given equilibrium reaction with substituent R and the reference constant ${K}_{0}$ when R is a hydrogen atom to the substituent constant $σ$ which depends only on the specific substituent R and the reaction rate constant ρ which depends only on the type of reaction but not on the substituent used.[4][3]

The equation also holds for reaction rates k of a series of reactions with substituted benzene derivatives:

\log {\frac {k}{k_{0}}}=\sigma \rho

In this equation ${k}_{0}$ is the reference reaction rate of the unsubstituted reactant, and k that of a substituted reactant.

A plot of $\log {\frac {K}{K_{0}}}$ for a given equilibrium versus $\log {\frac {k}{k_{0}}}$ for a given reaction rate with many differently substituted reactants will give a straight line.

Substituent constants

The starting point for the collection of the substituent constants is a chemical equilibrium for which the substituent constant is arbitrarily set to 0 and the reaction constant is set to 1: the deprotonation of benzoic acid or benzene carboxylic acid (R and R' both H) in water at 25 °C.

Scheme 1. Dissociation of benzoic acids

Substituent constants: *para* and *meta* substituted benzene rings.[3][6]
Substituent	para- effect	meta- effect
Dimethylamino	−0.83	−0.211
Amino	−0.66	−0.161
Butylamino	−0.51	−0.34
Hydroxy	−0.37	+0.12
Methoxy	−0.268	+0.115
Ethoxy	−0.25	+0.015
Methyl	−0.170	−0.069
Trimethylsilyl	−0.07	−0.04
None	0.000	0.000
Fluoro	+0.062	+0.337
Chloro	+0.227	+0.373
Bromo	+0.232	+0.393
Iodo	+0.276	+0.353
Ethoxycarbonyl	+0.45	+0.37
Trifluoromethyl	+0.54	+0.43
Cyano	+0.66	+0.56
Nitro	+0.778	+0.710

Having obtained a value for K₀, a series of equilibrium constants (K) are now determined based on the same process, but now with variation of the para substituent—for instance, {{{1}}} or {{{1}}}. These values, combined in the Hammett equation with K₀ and remembering that ρ = 1, give the para substituent constants compiled in table 1 for amine, methoxy, ethoxy, dimethylamino, methyl, fluorine, bromine, chlorine, iodine, nitro and cyano substituents. Repeating the process with meta-substituents afford the meta substituent constants. This treatment does not include ortho-substituents, which would introduce steric effects.

The σ values displayed in the Table above reveal certain substituent effects. With ρ = 1, the group of substituents with increasing positive values—notably cyano and nitro—cause the equilibrium constant to increase compared to the hydrogen reference, meaning that the acidity of the carboxylic acid (depicted on the left of the equation) has increased. These substituents stabilize the negative charge on the carboxylate oxygen atom by an electron-withdrawing inductive effect (-I) and also by a negative mesomeric effect (-M).

The next set of substituents are the halogens, for which the substituent effect is still positive but much more modest. The reason for this is that while the inductive effect is still negative, the mesomeric effect is positive, causing partial cancellation. The data also show that for these substituents, the meta effect is much larger than the para effect, due to the fact that the mesomeric effect is greatly reduced in a meta substituent. With meta substituents a carbon atom bearing the negative charge is further away from the carboxylic acid group (structure 2b).

This effect is depicted in scheme 3, where, in a para substituted arene 1a, one resonance structure 1b is a quinoid with positive charge on the X substituent, releasing electrons and thus destabilizing the Y substituent. This destabilizing effect is not possible when X has a meta orientation.

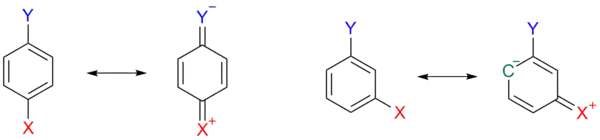
Scheme 3. Hammett Inductive Mesomeric Effects

Other substituents, like methoxy and ethoxy, can even have opposite signs for the substituent constant as a result of opposing inductive and mesomeric effect. Only alkyl and aryl substituents like methyl are electron-releasing in both respects.

Of course, when the sign for the reaction constant is negative (next section), only substituents with a likewise negative substituent constant will increase equilibrium constants.

The σ_p^– and σ_p⁺ constants

Because the carbonyl group is unable to serve a source of electrons for -M groups (in contrast to lone pair donors like OH), for reactions involving phenol and aniline starting materials, the σ_p values for electron-withdrawing groups will appear too small. For reactions where resonance effects are expected to have a major impact, a modified parameter, and a modified set of σ_p^– constants may give a better fit. This parameter is defined using the ionization constants of para substituted phenols, via a scaling factor to match up the values of σ_p^– with those of σ_p for "non-anomalous" substituents, so as to maintain comparable ρ values: for ArOH ⇄ ArO^– + H⁺, we define $\sigma _{p}^{-}={\frac {1}{2.11}}\log _{10}\left({\frac {K_{{\ce {X}}}}{K_{{\ce {H}}}}}\right)$ .

Likewise, the carbonyl carbon of a benzoic acid is at a nodal position and unable to serve as a sink for +M groups (in contrast to a carbocation at the benzylic position). Thus for reactions involving carbocations at the α-position, the σ_p values for electron-donating groups will appear insufficiently negative. Based on similar considerations, a set of σ_p⁺ constants give better fit for reactions involving electron-donating groups at the para position and the formation of a carbocation at the benzylic site. The σ_p⁺ are based on the rate constants of the S_N1 reaction of cumyl chlorides in 90% acetone/water: for ArCMe₂Cl + H₂O → ArCMe₂OH + HCl, we define $\sigma _{p}^{+}=-{\frac {1}{4.54}}\log _{10}\left({\frac {k_{{\ce {X}}}}{k_{{\ce {H}}}}}\right)$ . Note that the scaling factor is negative, since an electron-donating group speeds up the reaction. For a reaction whose Hammett plot is being constructed, these alternative Hammett constants may need to be tested to see if a better linearity could be obtained.

Rho value

With knowledge of substituent constants it is now possible to obtain reaction constants for a wide range of organic reactions. The archetypal reaction is the alkaline hydrolysis of ethyl benzoate (R=R'=H) in a water/ethanol mixture at 30 °C. Measurement of the reaction rate k₀ combined with that of many substituted ethyl benzoates ultimately result in a reaction constant of +2.498.[3]

Scheme 2. Hydrolysis of benzoic acid esters

Reaction constants are known for many other reactions and equilibria. Here is a selection of those provided by Hammett himself (with their values in parentheses):

the hydrolysis of substituted cinnamic acid ester in ethanol/water (+1.267)
the ionization of substituted phenols in water (+2.008)
the acid catalyzed esterification of substituted benzoic esters in ethanol (-0.085)
the acid catalyzed bromination of substituted acetophenones (Ketone halogenation) in an acetic acid/water/hydrochloric acid (+0.417)
the hydrolysis of substituted benzyl chlorides in acetone-water at 69.8 °C (-1.875).

The reaction constant, or sensitivity constant, ρ, describes the susceptibility of the reaction to substituents, compared to the ionization of benzoic acid. It is equivalent to the slope of the Hammett plot. Information on the reaction and the associated mechanism can be obtained based on the value obtained for ρ. If the value of:

ρ>1, the reaction is more sensitive to substituents than benzoic acid and negative charge is built during the reaction (or positive charge is lost).
0<ρ<1, the reaction is less sensitive to substituents than benzoic acid and negative charge is built (or positive charge is lost).
ρ=0, no sensitivity to substituents, and no charge is built or lost.
ρ<0, the reaction builds positive charge (or loses negative charge).

These relations can be exploited to elucidate the mechanism of a reaction. As the value of ρ is related to the charge during the rate determining step, mechanisms can be devised based on this information. If the mechanism for the reaction of an aromatic compound is thought to occur through one of two mechanisms, the compound can be modified with substituents with different σ values and kinetic measurements taken. Once these measurements have been made, a Hammett plot can be constructed to determine the value of ρ. If one of these mechanisms involves the formation of charge, this can be verified based on the ρ value. Conversely, if the Hammett plot shows that no charge is developed, i.e. a zero slope, the mechanism involving the building of charge can be discarded.

Hammett plots may not always be perfectly linear. For instance, a curve may show a sudden change in slope, or ρ value. In such a case, it is likely that the mechanism of the reaction changes upon adding a different substituent. Other deviations from linearity may be due to a change in the position of the transition state. In such a situation, certain substituents may cause the transition state to appear earlier (or later) in the reaction mechanism.[7]

Dominating electronic effects

3 kinds of ground state or static electrical influences predominate:

Resonance (mesomeric) effect
Inductive effect: electrical influence of a group which is transmitted primarily by polarization of the bonding electrons from one atom to the next
Direct electrostatic (field) effect: electrical influence of a polar or dipolar substituent which is transmitted primarily to the reactive group through space (including solvent, if any) according to the laws of classical electrostatics

The latter two influences are often treated together as a composite effect, but are treated here separately. Westheimer demonstrated that the electrical effects of π-substituted dipolar groups on the acidities of benzoic and phenylacetic acids can be quantitatively correlated, by assuming only direct electrostatic action of the substituent on the ionizable proton of the carboxyl group. Westheimer's treatment worked well except for those acids with substituents that have unshared electron pairs such as –OH and –OCH3, as these substituents interact strongly with the benzene ring.[8][9]

4-substituted bicyclo-2.2.2.-octane-1-carboxylic acid

Roberts and Moreland studied the reactivities of 4-substituted bicyclo[2.2.2]octane-1-carboxylic acids and esters. In such a molecule, transmission of electrical effects of substituents through the ring by resonance is not possible. Hence, this hints on the role of the π-electrons in the transmission of substituent effects through aromatic systems.[10]

Reactivity of 4-substituted bicyclo[2.2.2]octane-1-carboxylic acids and esters were measured in 3 different processes, each of which had been previously used with the benzoic acid derivatives. A plot of log(k) against log(K_A) showed a linear relationship. Such linear relationships correspond to linear free energy relationships, which strongly imply that the effect of the substituents are exerted through changes of potential energy and that the steric and entropy terms remain almost constant through the series. The linear relationship fit well in the Hammett Equation. For the 4-substituted bicyclo[2.2.2.]octane-1-carboxylic acid derivatives, the substituent and reaction constants are designated σ’ and ρ’.

Comparison of ρ and ρ’

Reaction	ρ'	ρ	D^e
Ionization of acids	1.464	1.464	54
Alkaline hydrolysis of ethyl esters	2.24	2.494	28
Acids with diphenyldiazomethane	0.698	0.937	24

Reactivity data indicate that the effects of substituent groups in determining the reactivities of substituted benzoic and bicyclo[2.2.2.]-octane-1-carboxylic acids are comparable. This implies that the aromatic π-electrons do not play a dominant role in the transmission of electrical effects of dipolar groups to the ionizable carboxyl group Difference between ρ and ρ’ for the reactions of the acids with diphenylazomethane is probably due to an inverse relation to the solvent dielectric constant D^e

Comparison of σ and σ’

Substituent	σ’	σ_para^c	σ_meta^c	σ_para − σ’	σ_meta − σ’
H	0	0	0	0	0
OH	0.283	−0.341	0.014	−0.624	−0.269
CO₂C₂H₅	0.297	0.402	0.334	0.105	0.037
Br	0.454	0.232	0.391	−0.222	−0.063
CN	0.579	0.656	0.608	0.077	0.029

For meta-directing groups (electron withdrawing group or EWG), σ_meta and σ_para are more positive than σ’. (The superscript, c, in table denotes data from Hammett, 1940.[11]) For ortho-para directing groups (electron donating group or EDG), σ’ more positive than σ_meta and σ_para. The difference between σ_para and σ’ (σ_para – σ’) is greater than that between σ_meta and σ’(σ_meta − σ’). This is expected as electron resonance effects are felt more strongly at the p-positions. The (σ – σ’) values can be taken as a reasonable measurement of the resonance effects.

Nonlinearity

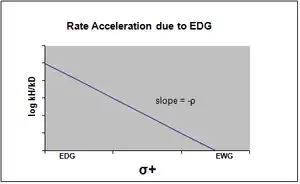
Rate acceleration EDG

The plot of the Hammett equation is typically seen as being linear, with either a positive or negative slope correlating to the value of rho. However, nonlinearity emerges in the Hammett plot when a substituent affects the rate of reaction or changes the rate-determining step or reaction mechanism of the reaction. For the reason of the former case, new sigma constants have been introduced to accommodate the deviation from linearity otherwise seen resulting from the effect of the substituent. σ+ takes into account positive charge buildup occurring in the transition state of the reaction. Therefore, an electron donating group (EDG) will accelerate the rate of the reaction by resonance stabilization and will give the following sigma plot with a negative rho value.[12]

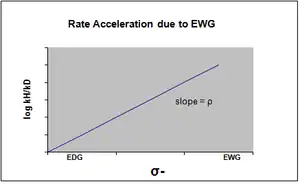
Rate acceleration EWG

σ- is designated in the case where negative charge buildup in the transition state occurs, and the rate of the reaction is consequently accelerated by electron withdrawing groups (EWG). The EWG withdraws electron density by resonance and effectively stabilizes the negative charge that is generated. The corresponding plot will show a positive rho value.

In the case of a nucleophilic acyl substitution the effect of the substituent, X, of the non-leaving group can in fact accelerate the rate of the nucleophilic addition reaction when X is an EWG. This is attributed to the resonance contribution of the EWG to withdraw electron density thereby increasing the susceptibility for nucleophilic attack on the carbonyl carbon. A change in rate occurs when X is EDG, as is evidenced when comparing the rates between X = Me and X = OMe, and nonlinearity is observed in the Hammett plot.[13]

The effect of the substituent may change the rate-determining step (rds) in the mechanism of the reaction. A certain electronic effect may accelerate a certain step so that it is no longer the rds.[14]

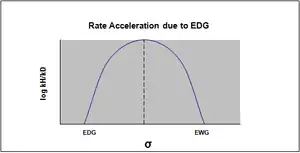
change in rate determining step

A change in the mechanism of a reaction also results in nonlinearity in the Hammett plot. Typically, the model used for measuring the changes in rate in this instance is that of the SN2 reaction.[15] However, it has been observed that in some cases of an SN2 reaction that an EWG does not accelerate the reaction as would be expected[16] and that the rate varies with the substituent. In fact, the sign of the charge and degree to which it develops will be affected by the substituent in the case of the benzylic system.[15]

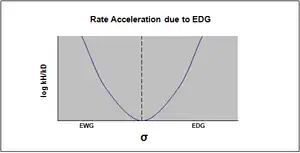
Change in emchanism

For example, the substituent may determine the mechanism to be an SN1 type reaction over a SN2 type reaction, in which case the resulting Hammett plot will indicate a rate acceleration due to an EDG, thus elucidating the mechanism of the reaction.

Another deviation from the regular Hammett equation is explained by the charge of nucleophile.[15] Despite nonlinearity in benzylic SN2 reactions, electron withdrawing groups could either accelerate or retard the reaction. If the nucleophile is negatively charged (e.g. cyanide) the electron withdrawing group will increase the rate due to stabilization of the extra charge which is put on the carbon in the transition state. On the other hand, if the nucleophile is not charged (e.g. triphenylphosphine), electron withdrawing group is going to slow down the reaction by decreasing the electron density in the anti bonding orbital of leaving group in the transition state.

Hammett modifications

Other equations now exist that refine the original Hammett equation: the Swain–Lupton equation, the Taft equation, the Grunwald–Winstein equation, and the Yukawa–Tsuno equation. An equation that addresses stereochemistry in aliphatic systems has also been developed.[17]

Estimation of Hammett sigma constants

Core-electron binding energy (CEBE) shifts correlate linearly with the Hammett substituent constants (σ) in substituted benzene derivatives.[18]

ΔCEBE \approx κσ p

(1)

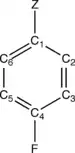
Consider para-disubstituted benzene p-F-C₆H₄-Z, where Z is a substituent such as NH₂, NO₂, etc. The fluorine atom is para with respect to the substituent Z in the benzene ring. The image on the right shows four distinguished ring carbon atoms, C1(ipso), C2(ortho), C3(meta), C4(para) in p-F-C₆H₄-Z molecule. The carbon with Z is defined as C1(ipso) and fluorinated carbon as C4(para). This definition is followed even for Z = H. The left-hand side of (1) is called CEBE shift or ΔCEBE, and is defined as the difference between the CEBE of the fluorinated carbon atom in p-F-C₆H₄-Z and that of the fluorinated carbon in the reference molecule FC₆H₅.

ΔCEBE ≡ CEBE(C4 in p-F-C₆H₄-Z) – CEBE(C4 in p-F-C₆H₅)

(2)

The right-hand side of Eq. 1 is a product of a parameter κ and a Hammett substituent constant at the para position, σp. The parameter $κ$ is defined by eq. 3:

κ = 2.3 kT (ρ - ρ *)

(3)

where $ρ$ and $ρ *$ are the Hammett reaction constants for the reaction of the neutral molecule and core ionized molecule, respectively. ΔCEBEs of ring carbons in p-F-C₆H₄-Z were calculated with density functional theory to see how they correlate with Hammett σ-constants. Linear plots were obtained when the calculated CEBE shifts at the ortho, meta and para carbon were plotted against Hammett σ_o, σ_m and σ_p constants respectively.

$κ$ value calculated ≈ 1.

Hence the approximate agreement in numerical value and in sign between the CEBE shifts and their corresponding Hammett σ constant.[19]

Plot of calculated CEBE shift (eV) against sigma-para
Table of CEBE shifts (eV) and sigma-para
Plot of calculated CEBE shift (eV) against sigma-meta
Table of CEBE shifts (eV) and sigma-meta
Plot of calculated CEBE shift (eV) against sigma-o
Table of CEBE shifts (eV) and sigma-ortho

Notes

The opening line in his 1935 publication reads: "The idea that there is some sort of relationship between the rate of a reaction and the equilibrium constant is one of the most persistently held and at the same time most emphatically denied concepts in chemical theory".[4]

References

IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Hammett equation (Hammett relation)". doi:10.1351/goldbook.H02732
Keenan, Sheue L.; Peterson, Karl P.; Peterson, Kelly; Jacobson, Kyle (2008). "Determination of Hammett Equation Rho Constant for the Hydrolysis of p-Nitrophenyl Benzoate Esters". J. Chem. Educ. 85 (4): 558. Bibcode:2008JChEd..85..558K. doi:10.1021/ed085p558.
Hammett, Louis P. (1937). "The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives". J. Am. Chem. Soc. 59 (1): 96–103. doi:10.1021/ja01280a022.
Louis P. Hammett (1935). "Some relations between Reaction Rates and Equilibrium Constants". Chem. Rev. 17 (1): 125–136. doi:10.1021/cr60056a010.
Carey, Francis A.; Sundberg, Richard J. (1983). Advanced Organic Chemistry Part A, 2nd edition. Plenum Press. ISBN 9780306410871. OCLC 1064985344.
Table values are this original 1937 publication, and differ from values appearing in subsequent publications. For more standard values, see: C. Hansch; A. Leo; R. W. Taft (1991). "A survey of Hammett substituent constants and resonance and field parameters". Chem. Rev. 91 (2): 165–195. doi:10.1021/cr00002a004. S2CID 97583278.
E.V. Anslyn & D.A. Dougherty, Modern Physical Organic Chemistry, pp. TBD, Sausalito, CA, US: University Science Books, ISBN 1891389319.
Westheimer F.H. (1939). "The Electrostatic effect of substituents on the dissociation constants of organic acids. IV. Aromatic acids". J. Am. Chem. Soc. 61 (8): 1977–1980. doi:10.1021/ja01877a012.
Kirkwood J.G.; Westheimer F.H. (1938). "The electrostatic influence of substituents on the dissociation constants of organic acids. I [Missing Subtitle]". J. Chem. Phys. 6 (9): 506. Bibcode:1938JChPh...6..506K. doi:10.1063/1.1750302.
Roberts J.D.; Moreland Jr. W.T. (1953). "Electrical Effects of Substituent Groups in Saturated Systems. Reactivities of 4-Substituted Bicyclo [2.2.2] octane-1-carboxylic acids". J. Am. Chem. Soc. 75 (9): 2167–2173. doi:10.1021/ja01105a045.
L.P.Hammett, 1940, "Chapter III," "Chapter IV," and "Chapter VII," in Physical Organic Chemistry, New York, NY, US: McGraw-Hill.
Y. Yukawa & Y. Tsuno, 1959, "Resonance Effect in Hammett Relationship. II. Sigma Constants in Electrophilic Reactions and their Intercorrelation," Bull. Chem. Soc. Jpn. 32:965-971, see , accessed 22 June 2015.
Um, Ik-Hwan; Lee, Ji-Youn; Kim, Han-Tae; Bae, Sun-Kun (2004). "Curved Hammett plot in alkaline hydrolysis of O-aryl thionobenzoates: Change in rate-determining step versus ground-state stabilization". J. Org. Chem. 69 (7): 2436–2441. doi:10.1021/jo035854r. PMID 15049643.
Hart, H.; Sedor, Edward A. (1967). "Mechanism of cyclodehydration of 2-phenyltriarylcarbinols". J. Am. Chem. Soc. 89 (10): 2342. doi:10.1021/ja00986a018.
Stein, Allan R.; Tencer, Michal; Moffatt, Elizabeth A.; Dawe, Robert; Sweet, James (1980). "Nonlinearity of Hammett .sigma..rho. correlations for benzylic systems: activation parameters and their mechanistic implications". J. Org. Chem. 45 (17): 3539–3540. doi:10.1021/jo01305a045.
Young, P. R.; Jencks, W. P. (1979). "Separation of polar and resonance substituent effects in the reactions of acetophenones with bisulfite and of benzyl halides with nucleophiles". J. Am. Chem. Soc. 101 (12): 3288. doi:10.1021/ja00506a025.
Bols, Mikael; Liang, Xifu; Jensen, Henrik H. (2002). "Equatorial contra axial polar substituents. The relation of a chemical reaction to stereochemical substituent constants". J. Org. Chem. 67 (25): 8970–4. doi:10.1021/jo0205356. PMID 12467416.
Linderberg, B.; Svensson, S.; Malmquist, P.A.; Basilier, E.; Gelius, U.; Siegbahn, K. (1976). "Correlation of ESCA shifts and Hammett substituent constants in substituted benzene derivatives". Chem. Phys. Lett. 40 (2): 175. Bibcode:1976CPL....40..175L. doi:10.1016/0009-2614(76)85053-1.
Takahata Y.; Chong D.P. (2005). "Estimation of Hammett sigma constants of substituted benzenes through accurate density-functional calculation of core-electron binding energy shifts". International Journal of Quantum Chemistry. 103 (5): 509–515. Bibcode:2005IJQC..103..509T. doi:10.1002/qua.20533.

Hammett equation