Guderley–Landau–Stanyukovich problem

The governing equations are

${\displaystyle {\begin{aligned}{\frac {\partial \rho }{\partial t}}+v{\frac {\partial \rho }{\partial r}}&=-\rho \left({\frac {\partial v}{\partial r}}+{\frac {2v}{r}}\right),\\{\frac {\partial v}{\partial t}}+v{\frac {\partial v}{\partial r}}&=-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}},\\{\frac {\partial s}{\partial t}}+v{\frac {\partial s}{\partial r}}&=0\end{aligned}}}$

where ${\displaystyle \rho }$ is the density, ${\displaystyle p}$ is the pressure, ${\displaystyle s}$ is the entropy and ${\displaystyle v}$ is the radial velocity. In place of the pressure ${\displaystyle p(r,t)}$, we can use the sound speed ${\displaystyle c(r,t)}$ using the relation ${\displaystyle c^{2}=\gamma p/\rho }$.

To obtain the self-similar equations, we introduce[3][4][5]

${\displaystyle \xi ={\frac {r}{R(t)}},\quad V(\xi )={\frac {vt}{\alpha r}},\quad G(\xi )={\frac {\rho }{\rho _{0}}},\quad Z(\xi )={\frac {c^{2}t^{2}}{\alpha ^{2}r^{2}}}.}$

Note that since both ${\displaystyle t}$ and ${\displaystyle v}$ are negative, ${\displaystyle V>0}$. Formally the solution has to be found for the range ${\displaystyle 1<\xi <\infty }$. The boundary conditions at ${\displaystyle \xi =1}$ are given by

${\displaystyle V(1)={\frac {2}{\gamma +1}},\quad G(1)={\frac {\gamma +1}{\gamma -1}},\quad Z(1)={\frac {2\gamma (\gamma -1)}{(\gamma +1)^{2}}}.}$

The boundary conditions at ${\displaystyle \xi =\infty }$ can be derived from the observation at the time of collapse ${\displaystyle t=0}$, wherein ${\displaystyle \xi }$ becomes infinite. At the moment of collapse, the flow variables at any distance from the origin must be finite, that is to say, ${\displaystyle v}$ and ${\displaystyle c^{2}}$ must be finite for ${\displaystyle t=0,\,r\neq 0}$. This is possible only if

${\displaystyle V(\infty )=0,\quad Z(\infty )=0.}$

Substituting the self-similar variables into the governing equations lead to

${\displaystyle {\begin{aligned}(1-V){\frac {dV}{d\ln \xi }}-{\frac {Z}{\gamma }}{\frac {d\ln G}{d\ln \xi }}-{\frac {1}{\gamma }}{\frac {dZ}{d\ln \xi }}&={\frac {2}{\gamma }}Z-V\left({\frac {1}{\alpha }}-V\right),\\{\frac {dV}{d\ln \xi }}-(1-V){\frac {d\ln G}{d\ln \xi }}&=-3V,\\(\gamma -1)Z{\frac {d\ln G}{d\ln \xi }}-{\frac {dZ}{d\ln \xi }}&={\frac {2Z}{1-Z}}\left({\frac {1}{\alpha }}-V\right).\end{aligned}}}$

From here, we can easily solve for ${\displaystyle d\ln G/d\ln \xi }$ and ${\displaystyle d\ln V/d\ln \xi }$ (or, ${\displaystyle d\ln Z/d\ln \xi }$) to find two equations. As a third equation, we could two of the equations by eliminating the variable ${\displaystyle \xi }$. The resultant equations are

${\displaystyle {\begin{aligned}{\frac {d\ln \xi }{dV}}&=-{\frac {\Delta }{\Delta _{1}}},\\(1-V){\frac {d\ln G}{d\ln \xi }}&=3V-{\frac {\Delta _{1}}{\Delta }},\\{\frac {dZ}{dV}}&={\frac {Z}{1-V}}\left\{{\frac {\Delta [2/\alpha -(3\gamma -1)V]}{\Delta _{1}}}+\gamma -1\right\}\end{aligned}}}$

where ${\displaystyle \Delta =Z-(1-V)^{2}}$ and ${\displaystyle \Delta _{1}=[3V-2(1-\alpha )/\alpha \gamma ]Z-V(1-V)(1/\alpha -V)}$. It can be easily seen once the third equation is solved for ${\displaystyle Z=Z(V)}$, the first two equations can be integrated using simple quadratures.

Guderley-Landau-Stanyukovich integral curve for ${\displaystyle \gamma =7/5}$

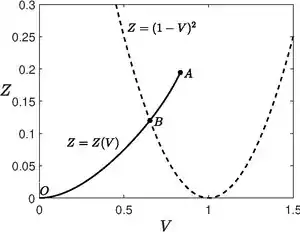
The third equation is first-order differential equation for the function ${\displaystyle Z(V)}$ with the boundary condition ${\displaystyle Z(2/(\gamma +1))=2\gamma (\gamma -1)/(\gamma +1)^{2}}$ pertaining to the condition behind the shock front. But there is another boundary condition that needs to be satisfied, i.e., ${\displaystyle Z(0)=0}$ pertaining to the condition found at ${\displaystyle \xi =\infty }$. This additional condition can be satisfied not for any arbitrary value of ${\displaystyle \alpha }$, but there exists only one value of ${\displaystyle \alpha }$ for which the second condition can be satisfied. Thus ${\displaystyle \alpha }$ is obtained as an eigenvalue. This eigenvalue can be obtained numerically.

The condition that determines ${\displaystyle \alpha }$ can be explained by plotting the integral curve ${\displaystyle Z=Z(V)}$ as shown in the figure as a solid curve. The point ${\displaystyle A}$ is the initial condition for the differential equation, i.e., ${\displaystyle A:(V,Z)=(2/(\gamma +1),2\gamma (\gamma -1)/(\gamma +1)^{2})}$. The integral curve must end at the point ${\displaystyle O:(V,Z)=(0,0)}$. In the same figure, the parabola ${\displaystyle Z=(1-V)^{2}}$ corresponding to the condition ${\displaystyle \Delta =0}$ is also plotted as a dotted curve. It can be easily shown than the point ${\displaystyle A}$ always lies above this parabola. This means that the integral curve ${\displaystyle Z=Z(V)}$ must intersect the parabola to reach the point ${\displaystyle O}$. In all the three differential equation, the ratio ${\displaystyle \Delta /\Delta _{1}}$ appears implying that this ratio vanishes at point ${\displaystyle B}$ where the integral curve intersects the parabola. The physical requirement for the functions ${\displaystyle V,\,G}$ and ${\displaystyle Z}$ is that they must be single-valued functions of ${\displaystyle \xi }$ to get a unique solution. This means that the functions ${\displaystyle \xi (V),\,\xi (G)}$ and ${\displaystyle \xi (Z)}$ cannot have extrema anywhere inside the domain. But at the point ${\displaystyle B}$, ${\displaystyle \Delta /\Delta _{1}}$ can vanish, indicating that the aforementioned functions have extrema. The only way to avoid this situation is to make the ratio ${\displaystyle \Delta /\Delta _{1}}$ at ${\displaystyle B}$ finite. That is to say, as ${\displaystyle \Delta }$ becomes zero, we require ${\displaystyle \Delta _{1}}$ also to be zero in such a manner to obtain ${\displaystyle \Delta /\Delta _{1}=0/0={\text{finite}}}$. At ${\displaystyle B}$,

${\displaystyle Z=(1-V)^{2},\quad (3V-2(1-\alpha )/\alpha \gamma )Z=V(1-V)(1/\alpha -V).}$

Numerical integrations of the third equation provide ${\displaystyle \alpha =0.6883740859}$ for ${\displaystyle \gamma =5/3}$ and ${\displaystyle \alpha =0.7171745015}$ for ${\displaystyle \gamma =7/5}$. These values for ${\displaystyle \alpha }$ may be compared with an approximate formula ${\displaystyle \alpha =[1+2\gamma /({\sqrt {\gamma }}+{\sqrt {2}})^{2}]^{-1}}$, derived by Landau and Stanyukovich. It can be established that as ${\displaystyle \gamma \rightarrow 1}$, ${\displaystyle \alpha \rightarrow 1}$. In general, the similarity index ${\displaystyle \alpha }$ is an irrational number.