Glissette
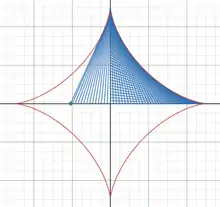
In geometry, a glissette is a curve determined by either the locus of any point, or the envelope of any line or curve, that is attached to a curve that slides against or along two other fixed curves.
Examples
Ellipse
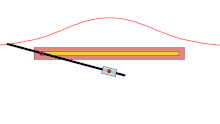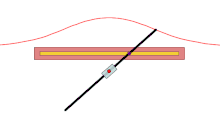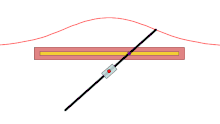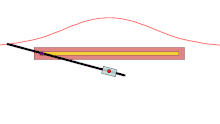
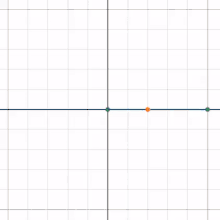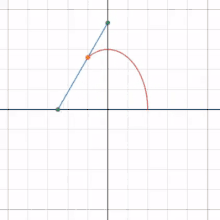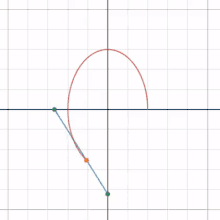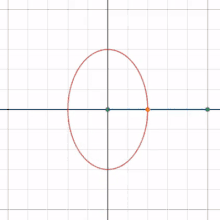
A basic example is that of a line segment of which the endpoints slide along two perpendicular lines. The glissette of any point on the line forms an ellipse.[1]
References
- Besant, William (1890). Notes on Roulettes and Glissettes. Deighton, Bell. p. 51. Retrieved 6 April 2017.
- Yates, Robert C. (1947). A Handbook on Curves and their Properties. Ann Arbor, MI: Edwards Bros. p. 109. Retrieved 6 April 2017.
- Lockwood, E. H. (1961). A Book of Curves (PDF). Cambridge University Press. p. 162. Retrieved 6 April 2017.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.