Geiringer–Laman theorem
The Geiringer–Laman theorem gives a combinatorial characterization of generically rigid graphs in -dimensional Euclidean space, with respect to bar-joint frameworks. This theorem was first proved by Hilda Pollaczek-Geiringer in 1927,[1] and later by Gerard Laman in 1970.[2] An efficient algorithm called the Pebble Game is used to identify this class of graphs.[3] This theorem has been the inspiration for many Geiringer-Laman type results for other types of frameworks with generalized Pebble games.[4]
Statement of the theorem
This theorem relies on definitions of genericity that can be found on the structural rigidity page. Let denote the vertex set of a set of edges .
Geiringer-Laman Theorem. [1][2] A graph is generically rigid in -dimensions with respect to bar-joint frameworks if and only if has a spanning subgraph such that
- for all subsets , .
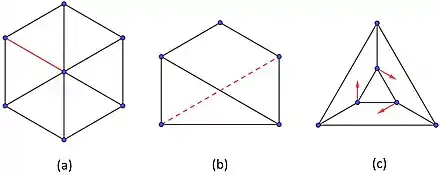
The spanning subgraph satisfying the conditions of the theorem is called a Geiringer-Laman, or minimally rigid, graph. Graphs satisfying the second condition form the independent sets of a sparsity matroid, and are called -sparse. A graph satisfying both conditions is also called a -tight graph. The direction of the theorem which states that a generically rigid graph is -tight is called the Maxwell direction, because James Clerk Maxwell gave an analogous necessary condition of -sparsity for a graph to be independent in the -dimensional generic rigidity matroid.[5] The other direction of the theorem is the more difficult direction to prove. For dimensions , a graph that is -tight is not necessarily generically minimally rigid, i.e., the converse of the Maxwell Direction is not true.
Example. Consider the graphs in Figure 1. The graph in (c) is generically minimally rigid, but it is not infinitesimally rigid. The red velocity vectors depict a non-trivial infinitesimal flex. Removing the red edge in (a) yields a generically minimally rigid spanning graph. Adding the dashed red edge in (b) makes the graph generically minimally rigid.
Theorem. Let be a graph. The following statements are equivalent:
- is a generically minimally rigid;
- is -tight; and
- contains three edge-disjoint spanning trees and such that (i) each vertex of is contained in exactly two of these spanning trees and (ii) distinct subtrees of these spanning trees do not have the same vertex set.
The equivalence of the first and second statements is the Geiringer-Laman theorem. The equivalence of the first and third statements was first proved by,[6] via the Geiringer-Laman theorem , and later in,[7] via a more direct approach.
Outline of proof
The proof of the Geiringer-Laman theorem given below is based on Laman's proof.[2] Furthermore, the details of the proofs below are based on lecture notes found here [8]
Consider a bar-joint system and a framework of this system, where is a map that places the vertices of in the plane such that the distance constraints are satisfied. For convenience, we refer to as a framework of . The proof of the Geiringer-Laman theorem follows the outline below.
- A graph is generically rigid if and only if it is generically infinitesimally rigid.
- Infinitesimal rigidity is a generic property of graphs.
- Rigidity is a generic property of graphs.
- If a framework is infinitesimally rigid, then it is rigid.
- If a framework is generic with respect to infinitesimally rigidity and rigid, then it is infinitesimally rigid.
- If a graph has a generic infinitesimally rigid framework, then is a Geiringer-Laman graph.
- A graph is a Geiringer-Laman graph if and only if has a Henneberg construction.
- If a graph has a Henneberg construction, then has a generic infinitesimally rigid framework.
Step 1 sets up the generic setting of rigidity so that we can focus on generic infinitesimal rigidity rather than generic rigidity. This is an easier approach, because infinitesimal rigidity involves a system of linear equations, rather than quadratic in the case of regular rigidity. In particular, we can prove structural properties about the rigidity matrix of a generic framework. These results were first proved by Asimow and Roth,[9][10] see Combinatorial characterizations of generically rigid graphs. Note that in Step 1.4 the framework must be generic with respect to infinitesimal rigidity. In particular, a framework that is rigid and generic with respect to rigidity is not necessarily infinitesimally rigid. Step 2 is the Maxwell Direction of the proof, which follows from simple counting arguments on the rigidity matrix. Step 3 shows that generically minimally rigid graphs are exactly the graphs that can be constructed starting from a single edge using two simple operations, which are defined below. Step 4 shows that graphs with this type of construction are generically infinitesimally rigid. Finally, once Step 1 is proved, Steps 2-3 prove the Geiringer-Laman theorem.
Equivalence of generic rigidity and generic infinitesimal rigidity
Let be a graph. First, we show that generic frameworks with respect to infinitesimal rigidity form an open and dense set in . One necessary and sufficient condition for a framework of to be infinitesimally rigid is for its rigidity matrix to have max rank over all frameworks of .
Proposition 1. For any framework of and any neighborhood , there exists a framework in such that the rigidity matrix has max rank.
Proof. If the rigidity matrix does not have max rank, then it has a set of dependent rows corresponding to a subset of edges such that for some other rigidity matrix , the rows corresponding to are independent. Let be the set of frameworks such that the rows corresponding to in their rigidity matrices are dependent. In other words, is the set of frameworks such that the minor of the rows corresponding to in is . Hence, is a curve in , because a minor is a polynomial in the entries of a matrix. Let be the union of these curves over all subsets of edges of . If a framework does not have max rank for some framework , then is contained in . Finally, since is a finite set of curves, the proposition is proved.
Proposition 2. Infinitesimal rigidity is a generic property of graphs.
Proof. We show that if one generic framework with respect to infinitesimal rigidity is infinitesimally rigid, then all generic frameworks are infinitesimally rigid. If a framework of a graph is infinitesimally rigid, then has max rank. Note that the kernel of the rigidity matrix is the space of infinitesimal motions of a framework, which has dimension for infinitesimally rigid frameworks. Hence, by the Rank–nullity theorem, if one generic framework is infinitesimally rigid then all generic frameworks are infinitesimal rigidity have rigid.
Proposition 3. If a framework of a graph is infinitesimally rigid, then it is rigid.
Proof. Assume that is not rigid, so there exists a framework in a neighborhood such that and is cannot be obtained via a trivial motion of . Since is in , there exists a and such that . Applying some algebra yields:
Hence,
We can choose a sequence of such that and . This causes and . Hence,
The first and last expressions in the equations above state that is an infinitesimal motion of the framework . Since there is no trivial motion between and , is not a trivial infinitesimal motion. Thus, is not infinitesimally rigid.
Proposition 4. If a framework of a graph is rigid and generic with respect to infinitesimal rigidity, then is infinitesimally rigid.
Proof. This follows from the implicit function theorem. First, we will factor out all trivial motions of . Since has max rank, no points of are colinear. Hence, we can pin points of to factor out trivial motions: one point at the origin and another along the -axis at a distance from the origin consistent with all constraints. This yields a pinned framework that lives in . This can be done for all frameworks in a neighborhood of to obtain a neighborhood of of pinned frameworks. The set of such frameworks is still a smooth manifold, so the rigidity map and rigidity matrix can be redefined on the new domain. Specifically, the rigidity matrix of a pinned framework has columns and rank equal to , where is the unpinned framework corresponding to . In this pinned setting, a framework is rigid if it is the only nearby solution to the rigidity map.
Now, assume an unpinned framework is not infinitesimally rigid, so that . Then the , where is the pinned version of . We now set up to apply the implicit function theorem. Our continuously differentiable function is the rigidity map . The Jacobian of is the rigidity matrix. Consider the subset of edges corresponding to the independent rows of , yielding the submatrix . We can find independent columns of . Denote the entries in these columns by the vectors . Denote the entries of the remaining columns by the vectors . The submatrix of induced the is invertible, so by the implicit function theorem, there exists a continuously differentiable function such that and . Hence, the framework of the subgraph is not rigid, and since the rows of span the row space of , is also not rigid. This contradicts our assumption, so is infinitesimally rigid.
Proposition 5. Rigidity is a generic property of graphs.
Proof. Let be a rigid framework of that is generic with respect to rigidity. By definition, there is a neighborhood of rigid frameworks of . By Proposition 1, there is a framework in that is generic with respect to infinitesimal rigidity, so by Proposition 4, is infinitesimally rigid. Hence, by Proposition 2, all frameworks that are generic with respect to infinitesimal rigidity are infinitesimally rigid, and by Proposition 3 they are also rigid. Finally, every neighborhood of every framework that is generic with respect to rigidity contains a framework that is generic with respect to infinitesimal rigidity, by Proposition 1. Thus, if is rigid then is rigid.
Theorem 1. A graph is generically rigid if and only if it is generically infinitesimally rigid.
Proof. The proof follows a similar argument to the proof of Proposition 5. If is generically rigid, then there exists a generic framework with respect to rigidity that is rigid by definition. By Propositions 1 and 4, in any neighborhood of there is a framework that is generic with respect to infinitesimal rigidity and infinitesimally rigid. Hence, by Proposition 2, is generically infinitesimally rigid.
For the other direction, assume to the contrary that is generically infinitesimally rigid, but not generically rigid. Then there exists a generic framework with respect to rigidity that is not rigid by definition. By Proposition 1, in any neighborhood of there is a framework that is generic with respect to infinitesimal rigidity. By assumption is infinitesimally rigid, and by Proposition 3, is also rigid. Thus, must be rigid and, by Proposition 5, all frameworks that are generic with respect to rigidity are rigid. This contradicts our assumption that is not generically rigid.
Maxwell direction
The Maxwell Direction of the Geiringer-Laman theorem follows from a simple counting argument on the rigidity matrix.
Maxwell Direction. If a graph has a generic infinitesimally rigid framework, then has a Geiringer-Laman subgraph.
Proof. Let be a generic infinitesimally rigid framework of . By definition, has max rank, i.e., . In particular, has independent rows. Each row of corresponds to an edge of , so the submatrix with just the independent rows corresponds to a subgraph such that . Furthermore, any subgraph of corresponds to a submatrix of . Since the rows of are independent, so are the rows of . Hence, , which clearly satisfies .
Equivalence of generic infinitesimal rigidity and Henneberg constructions
Now we begin the proof of the other direction of the Geiringer-Laman theorem by first showing that a generically minimally rigid graph has a Henneberg construction. A Henneberg graph has the following recursive definition:
- is a single edge or
- can be obtained from a Henneberg graph via one of the following operations
- add a vertex to and connect it to distinct vertices of
- For an edge and a vertex of , add a vertex to , connect it to and , and then remove .
The two operations above are called a -extension and a -extension respectively.
The following propositions are proved in:[2]
Proposition 6. A generically minimally rigid graph has no vertex with degree and at least one vertex with degree less than
Proposition 7. If is a generically minimally rigid graph with a vertex of degree , connected to vertices and , then for at least one pair of the neighbors of , without loss of generality say , there is no subgraph of that contains and and satisfies .
Theorem 2. A generically minimally rigid graph with at least vertices has a Henneberg construction.
Proof. We proceed by induction on the number of vertices . The base case of is the base case Henneberg graph. Assume has a Henneberg construction when and we will prove it for . When , has a vertex with degree or , by Proposition 6.
Case 1: has degree 2.
Let be the subgraph of obtained by removing , so and . Since is minimally rigid, we have
Furthermore, any subgraph of is also a subgraph of , so by assumption. Hence, is minimally rigid, by the Maxwell Direction, and has a Henneberg construction by the inductive hypothesis. Now simply notice that can be obtained from via a -extension.
Case 2: has degree 3.
Let the edges incident to be and . By Proposition 7, for one pair of the neighbors of , without loss of generality say , there is no subgraph of that contains and and satisfies . Note that cannot be an edge, or else the subgraph on just that edge satisfies the previous equality. Consider the graph obtained by removing from and adding the edge . We have
.
Furthermore, as with Case 1, any subgraph of that does not contain satisfies the second condition for minimal rigidity by assumption. For a subgraph of that does contain , removing this edge yields a subgraph of . By Proposition 7, , so . Hence, is minimally rigid, and has a Henneberg construction by the inductive hypothesis. Finally, notice that can be obtained from via a -extension.
Combining Cases 1 and 2 proves the theorem by induction.
It is also easy to the converse of Theorem 2 by induction.
Proposition 8. A graph with a Henneberg construction is generically minimally rigid.
Henneberg constructible graphs are generically infinitesimally rigid
To complete the proof of the Geringer-Laman theorem, we show that if a graph has a Henneberg construction then it is generically infinitesimmaly rigid. The proof of this result relies on the following proposition from.[2]
Proposition 9. If are three non-colinear -dimensional points and are three -dimensional vectors, then the following statements are equivalent:
- for all
- The function
vanishes at every point .
Theorem 3. If a graph with at least vertices has a Henneberg construction, then is generically infinitesimally rigid.
Proof. We proceed by induction on the number of vertices . The graph in the base case is a triangle, which is generically infinitesimally rigid. Assume that when is generically infinitesimally rigid and we will prove it for . For , consider the graph that was obtained from via - or -extension. By the inductive hypothesis, is generically infinitesimally rigid. Hence, has a generic infinitesimally rigid framework such that the kernel of has dimension . Let be the vertex added to to obtain . We must choose a placement in -dimensions such that is a generic infinitesimally rigid framework of .
Case 1: is obtained from via a -extension.
Choosing such a placement for is equivalent to adding rows corresponding to the equations
to the rigidity matrix , where and are the neighbors of after the -extension and is the velocity assigned to by an infinitesimal motion. Our goal is to choose such the dimension of the space of infinitesimal motions of is the same as that of . We can choose such that it is not colinear to and , which ensures that there is only one solution to these equations. Hence, the kernel of has dimension , so is a generic infinitesimally rigid framework of .
Case 2: is obtained from via a -extension.
Let the neighbors of after the -extension be the edges , and , and let be the edge that was removed. Removing the edge from yields the subgraph . Let be the framework of that is equivalent to , except for the removed edge. The rigidity matrix can be obtained from by removing the row corresponding to the removed edge. By Proposition 8, is generically minimally rigid, so the rows of are independent. Hence, the rows of are independent and its kernel has dimension . Let be a basis vector for the space of infinitesimal motions of such that is a basis for the space of trivial infinitesimal motions. Then, any infinitesimal motion of can be written as a linear combination of these basis vectors. Choosing a placement for that results in a generic infinitesimally rigid framework of is equivalent to adding rows corresponding to the equations
to the rigidity matrix . Our goal is to choose such the dimension of the space of infinitesimal motions of is less than that of . After rearranging, these equations have a solution if and only if
Note that can be written as , for constants . Furthermore, we can move the summation outside of the determinant to obtain
Since form a basis for the trivial infinitesimal motions, the first three terms in the summation are , leaving only
Solutions to this equation form a curve in -dimensions. We can choose not along this curve so that , which ensures that there is only one solution to this equation. Hence, by Proposition 9, the kernel of has dimension , so is a generic infinitesimally rigid framework of .
Combining Cases 1 and 2 proves the theorem by induction.
See also
References
- Pollaczek‐Geiringer, H. (1927). "Über die Gliederung ebener Fachwerke". ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik. 7 (1): 58–72. Bibcode:1927ZaMM....7...58P. doi:10.1002/zamm.19270070107. ISSN 1521-4001.
- Laman, G. (1970-10-01). "On graphs and rigidity of plane skeletal structures". Journal of Engineering Mathematics. 4 (4): 331–340. Bibcode:1970JEnMa...4..331L. doi:10.1007/BF01534980. ISSN 1573-2703. S2CID 122631794.
- Jacobs, Donald J.; Hendrickson, Bruce (1997-11-01). "An Algorithm for Two-Dimensional Rigidity Percolation: The Pebble Game". Journal of Computational Physics. 137 (2): 346–365. Bibcode:1997JCoPh.137..346J. doi:10.1006/jcph.1997.5809. ISSN 0021-9991.
- Lee, Audrey; Streinu, Ileana (2008-04-28). "Pebble game algorithms and sparse graphs". Discrete Mathematics. 308 (8): 1425–1437. arXiv:math/0702129. doi:10.1016/j.disc.2007.07.104. ISSN 0012-365X. S2CID 2826.
- F.R.S, J. Clerk Maxwell (1864-04-01). "XLV. On reciprocal figures and diagrams of forces". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 27 (182): 250–261. doi:10.1080/14786446408643663. ISSN 1941-5982.
- Crapo, Henry (1990). "On the generic rigidity of plane frameworks". Preprint.
- Tay, Tiong-Seng (1993-06-01). "A new proof of laman's theorem". Graphs and Combinatorics. 9 (2): 365–370. doi:10.1007/BF02988323. ISSN 1435-5914. S2CID 40384855.
- Sitharam, Meera; Cheng, Jialong; Wang, Menghan (2011). "Notes 7 to 12". Lecture Notes – via University of Florida.
- Asimow, L.; Roth, B. (1978). "The rigidity of graphs". Transactions of the American Mathematical Society. 245: 279–289. doi:10.1090/S0002-9947-1978-0511410-9. ISSN 0002-9947.
- Asimow, L; Roth, B (1979-03-01). "The rigidity of graphs, II". Journal of Mathematical Analysis and Applications. 68 (1): 171–190. doi:10.1016/0022-247X(79)90108-2. ISSN 0022-247X.