Rank–nullity theorem
The rank–nullity theorem is a theorem in linear algebra, which asserts:
- the number of columns of a matrix M is the sum of the rank of M and the nullity of M; and
- the dimension of the domain of a linear transformation f is the sum of the rank of f (the dimension of the image of f) and the nullity of f (the dimension of the kernel of f).[1][2][3][4]
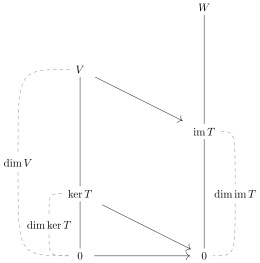
It follows that for linear transformations of vector spaces of equal finite dimension, either injectivity or surjectivity implies bijectivity.
Stating the theorem
Linear transformations
Let be a linear transformation between two vector spaces where 's domain is finite dimensional. Then
where is the rank of (the dimension of its image) and is the nullity of (the dimension of its kernel). In other words,
This theorem can be refined via the splitting lemma to be a statement about an isomorphism of spaces, not just dimensions. Explicitly, since induces an isomorphism from to the existence of a basis for that extends any given basis of implies, via the splitting lemma, that Taking dimensions, the rank–nullity theorem follows.
Proofs
Here we provide two proofs. The first[2] operates in the general case, using linear maps. The second proof[6] looks at the homogeneous system where is a with rank and shows explicitly that there exists a set of linearly independent solutions that span the null space of .
While the theorem requires that the domain of the linear map be finite-dimensional, there is no such assumption on the codomain. This means that there are linear maps not given by matrices for which the theorem applies. Despite this, the first proof is not actually more general than the second: since the image of the linear map is finite-dimensional, we can represent the map from its domain to its image by a matrix, prove the theorem for that matrix, then compose with the inclusion of the image into the full codomain.
First proof
Let be vector spaces over some field and defined as in the statement of the theorem with .
As is a subspace, there exists a basis for it. Suppose and let
be such a basis.
We may now, by the Steinitz exchange lemma, extend with linearly independent vectors to form a full basis of .
Let
such that
is a basis for . From this, we know that
We now claim that is a basis for . The above equality already states that is a generating set for ; it remains to be shown that it is also linearly independent to conclude that it is a basis.
Suppose is not linearly independent, and let
for some .
Thus, owing to the linearity of , it follows that
This is a contradiction to being a basis, unless all are equal to zero. This shows that is linearly independent, and more specifically that it is a basis for .
To summarize, we have , a basis for , and , a basis for .
Finally we may state that
This concludes our proof.
Second proof
Let be an matrix with linearly independent columns (i.e. ). We will show that:
- There exists a set of linearly independent solutions to the homogeneous system .
- That every other solution is a linear combination of these solutions.
To do this, we will produce an matrix whose columns form a basis of the null space of .
Without loss of generality, assume that the first columns of are linearly independent. So, we can write
where
- is an matrix with linearly independent column vectors, and
- is an matrix such that each of its columns is linear combinations of the columns of .
This means that for some matrix (see rank factorization) and, hence,
Let
where is the identity matrix. So, is an matrix such that
Therefore, each of the columns of are particular solutions of .
Furthermore, the columns of are linearly independent because will imply for :
Therefore, the column vectors of constitute a set of linearly independent solutions for .
We next prove that any solution of must be a linear combination of the columns of .
For this, let
be any vector such that . Since the columns of are linearly independent, implies .
Therefore,
This proves that any vector that is a solution of must be a linear combination of the special solutions given by the columns of . And we have already seen that the columns of are linearly independent. Hence, the columns of constitute a basis for the null space of . Therefore, the nullity of is . Since equals rank of , it follows that . This concludes our proof.
A third fundamental subspace
When is a linear transformation between two finite-dimensional subspaces, with and (so can be represented by an matrix ), the rank–nullity theorem asserts that if has rank , then is the dimension of the null space of , which represents the kernel of . In some texts, a third fundamental subspace associated to is considered alongside its image and kernel: the cokernel of is the quotient space , and its dimension is . This dimension formula (which might also be rendered ) together with the rank–nullity theorem is sometimes called the fundamental theorem of linear algebra.[7][8]
Reformulations and generalizations
This theorem is a statement of the first isomorphism theorem of algebra for the case of vector spaces; it generalizes to the splitting lemma.
In more modern language, the theorem can also be phrased as saying that each short exact sequence of vector spaces splits. Explicitly, given that
is a short exact sequence of vector spaces, then , hence
Here plays the role of and is , i.e.
In the finite-dimensional case, this formulation is susceptible to a generalization: if
is an exact sequence of finite-dimensional vector spaces, then[9]
The rank–nullity theorem for finite-dimensional vector spaces may also be formulated in terms of the index of a linear map. The index of a linear map , where and are finite-dimensional, is defined by
Intuitively, is the number of independent solutions of the equation , and is the number of independent restrictions that have to be put on to make solvable. The rank–nullity theorem for finite-dimensional vector spaces is equivalent to the statement
We see that we can easily read off the index of the linear map from the involved spaces, without any need to analyze in detail. This effect also occurs in a much deeper result: the Atiyah–Singer index theorem states that the index of certain differential operators can be read off the geometry of the involved spaces.
Citations
- Axler (2015) p. 63, §3.22
- Friedberg, Insel & Spence (2014) p. 70, §2.1, Theorem 2.3
- Katznelson & Katznelson (2008) p. 52, §2.5.1
- Valenza (1993) p. 71, §4.3
- Friedberg, Insel & Spence (2014) pp. 103-104, §2.4, Theorem 2.20
- Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388
-
- Strang, Gilbert. Linear Algebra and Its Applications. 3rd ed. Orlando: Saunders, 1988.
- Strang, Gilbert (1993), "The fundamental theorem of linear algebra" (PDF), American Mathematical Monthly, 100 (9): 848–855, CiteSeerX 10.1.1.384.2309, doi:10.2307/2324660, JSTOR 2324660
- Zaman, Ragib. "Dimensions of vector spaces in an exact sequence". Mathematics Stack Exchange. Retrieved 27 October 2015.
References
- Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388
- Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E. (2014). Linear Algebra (4th ed.). Pearson Education. ISBN 978-0130084514.
- Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8.
- Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
- Valenza, Robert J. (1993) [1951]. Linear Algebra: An Introduction to Abstract Mathematics. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 3-540-94099-5.
External links
- Gilbert Strang, MIT Linear Algebra Lecture on the Four Fundamental Subspaces, from MIT OpenCourseWare