Firoozbakht's conjecture

In number theory, Firoozbakht's conjecture (or the Firoozbakht conjecture[1][2]) is a conjecture about the distribution of prime numbers. It is named after the Iranian mathematician Farideh Firoozbakht who stated it first in 1982.

Prime gap function

The conjecture states that ${\displaystyle p_{n}^{1/n}}$ (where ${\displaystyle p_{n}}$ is the nth prime) is a strictly decreasing function of n, i.e.,

${\displaystyle {\sqrt[{n+1}]{p_{n+1}}}<{\sqrt[{n}]{p_{n}}}\qquad {\text{ for all }}n\geq 1.}$

Equivalently:

${\displaystyle p_{n+1}<p_{n}^{1+{\frac {1}{n}}}\qquad {\text{ for all }}n\geq 1,}$

see OEIS: A182134, OEIS: A246782.

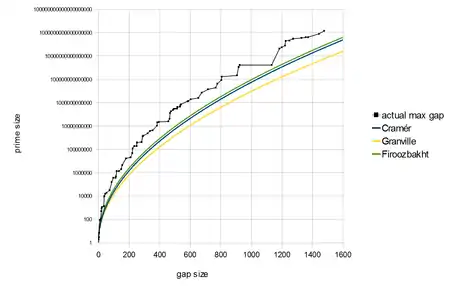
By using a table of maximal gaps, Farideh Firoozbakht verified her conjecture up to 4.444×10¹².[2] Now with more extensive tables of maximal gaps, the conjecture has been verified for all primes below 2⁶⁴ ≈ 1.84×10¹⁹.[3][4]

If the conjecture were true, then the prime gap function ${\displaystyle g_{n}=p_{n+1}-p_{n}}$ would satisfy:[5]

${\displaystyle g_{n}<(\log p_{n})^{2}-\log p_{n}\qquad {\text{ for all }}n>4.}$

Moreover:[6]

${\displaystyle g_{n}<(\log p_{n})^{2}-\log p_{n}-1\qquad {\text{ for all }}n>9,}$

see also OEIS: A111943. This is among the strongest upper bounds conjectured for prime gaps, even somewhat stronger than the Cramér and Shanks conjectures.[4] It implies a strong form of Cramér's conjecture and is hence inconsistent with the heuristics of Granville and Pintz[7][8][9] and of Maier[10][11] which suggest that

${\displaystyle g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}\approx 1.1229(\log p_{n})^{2},}$

occurs infinitely often for any ${\displaystyle \varepsilon >0,}$ where ${\displaystyle \gamma }$ denotes the Euler–Mascheroni constant.

Two related conjectures (see the comments of OEIS: A182514) are

${\displaystyle \left({\frac {\log(p_{n+1})}{\log(p_{n})}}\right)^{n}<e,}$

which is weaker, and

${\displaystyle \left({\frac {p_{n+1}}{p_{n}}}\right)^{n}<n\log(n)\qquad {\text{ for all }}n>5,}$

which is stronger.