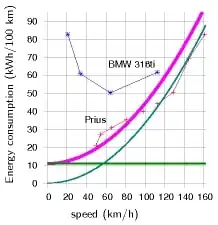
Car speed and energy consumption

The energy consumption of a car covering a given distance depends mainly on the speed of the vehicle. The faster a car drives, the more energy is required for propulsion. At higher speed the energy consumption of a car per unit distance increases proportional to the square of the speed.[1][2] This is caused by the air drag which dominates over the tyre rolling resistance at high speeds.[1][3][4]

A car splashes through a minor flood on Henbury Road, Bristol, 2012. Here the car loses energy due to air and water resistance and rolling resistance on the road surface which should all be accounted for in a calculation of the required car energy.

Driving twice as fast therefore costs approximately four times as much fuel per unit of distance. The required power increases with the cube of the speed, so driving twice as fast costs theoretically eight times as much fuel per unit of time.

Fuel consumption by a traditional car causes air pollution by combustion. This air pollution produced over a given distance likewise increases quadratically with increasing speed. Neglecting details, reducing the speed from 130 to 100 km/hour entails theoretically that only a relative fraction of (100/130)² = 0.59 = 59% of energy is expended, so that 41% less fuel is consumed over the same distance. This leads to a comparable reduction in air pollution from gasoline combustion.

Calculation

Plot of the energy a car consumes versus its speed. Air resistance is the main cause of the car fuel consumption (expended energy per distance) when driving at high steady speeds. Assumptions: the car's engine uses energy with an efficiency of 0.25, whatever the speed;

c_{d}\cdot A_{car}

= 1 m², and

m_{car}

= 1000 kg, and

C_{rr}

= 0.01. From David J.C. MacKay: Sustainable energy - without the hot air (2009), page 259, Figure 321.

At low speeds, the fuel consumption of Prius and BMW 318ti cars do not vary proportional to the square of their speeds. However at higher speeds, the Prius data approximately do. From David J.C. MacKay: Sustainable energy - without the hot air (2009), page 260, Figure 256.

The energy $E_{\text{motor}}$ for propulsion supplied by a car's engine is spent on:[5]

accelerating the car (abbreviated to ac),
overcoming the air resistance (aerodynamic drag, dr), and
overcoming the rolling resistance (rr).

so that

E_{\text{motor}}=E_{\text{ac}}+E_{\text{dr}}+E_{\text{rr}}

The energy effects of wind, ascent and descent are not considered here, nor the repeated braking and accelerating when driving in a city.

Acceleration

The kinetic energy $E_{\text{kin}}$ of a moving car with mass $m_{car}$ and speed $v_{car}$ can be calculated theoretically as[6][7]

E_{\text{kin}}={\tfrac {1}{2}}m_{car}\cdot v_{car}^{2}

so for a car with a mass of 1,000 kg at a speed of 120 km/h (33.3 m/s)

E_{\text{kin}}=0{.}5\times 1000\times 33{.}3^{2}=5{.}56\times 10^{5}\,{\text{J}}=0{.}15\,{\text{kWh}}

(One kilowatt hour (kWh) equals 3.6 million joules (J).[8])

The required kinetic energy is supplied by the motor when the car accelerates starting from rest. It is lost when the driver brakes (unless the available kinetic energy is stored in, for example, a flywheel). Part of this energy can also be recovered from electric cars via recuperative braking and can be stored in a accumulator.[9]

In practice, the real energy consumption of a car depends on many additional factors, including the traffic situation and personal driving style. In order to be able to make comparisons, standardized consumption tests have been devised, driving cycles, such as the New European Driving Cycle (NEDC) and the newer Worldwide harmonized Light vehicles Test Procedures (WLTP).

Without any resistance or friction, by Newton's First Law a car with speed $v$ would continue at this speed forever. However, air drag and rolling resistance cause energy losses which must be overcome to drive at a constant speed.

Air drag

Depending on its surface area $A_{car}$ , streamlining and speed $v$ , a car moves a lot of air, which causes energy loss by the aerodynamic drag force.[10] We can imagine the moving air as a tube (trunk) of air behind the car, with a volume of the cross-sectional area of that tube times the length, which equals the distance traveled by the car. This length is then equal to the car speed times the elapsed time. The effective cross-section of the air tube is less than the front surface of the car $A_{car}$ , for example due to streamlining. This can be taken in account by introducing a drag coefficient $c_{drag}$ for the air resistance of about 1/3.[11]
Suppose the surface area of the wind shield of a car is

A_{car}=2m\times 1.5m=3m^{2}

[12]

then the effective volume $V_{eff-air}$ of that tube of swirling air behind the car, after a period of driving $t$ at speed $v$ equals[12]

V_{eff-air}=A_{car}\cdot tubelength=A_{car}\cdot c_{drag}\cdot v_{car}\cdot t

with $v_{car}\cdot t$ = $d$ the distance traveled.
The mass of the displaced air over a journey of $d$ meters is equal to the volume of the tube times the specific mass $\rho _{air}$ of air, so

m_{air}=V_{eff-air}\cdot \rho _{air}=3\times 1/3\cdot d\cdot \rho _{air}

.

The energy loss due to air resistance is equal to the kinetic energy that the car imparts to the air:

E_{drag}={\tfrac {1}{2}}m_{air}\cdot v_{car}^{2}={\tfrac {1}{2}}\rho _{air}\cdot A_{car}\cdot d\cdot c_{drag}\cdot v_{car}^{2}\cong 0.65\cdot v_{car}^{2}\cdot d

Rolling resistance

The mathematical formula for the force due to the rolling resistance of the car tyres is:[13]

F_{rr}=C_{rr}\cdot m\cdot g

with

C_{rr}

the roll coefficient which is around 0.01.[14]

m

the mass of the car, and

g

the gravitational acceleration.

The corresponding energy loss caused by the rolling resistance is (the work done by the rolling resistance)[15]

E_{rr}=F_{rr}\cdot d=constant\cdot d

,

with $d$ the distance covered, so the energy spent on overcoming the rolling resistance per unit distance is a constant.

Total energy consumption to overcome friction

Adding up the energy consumption required to overcome both air drag and tyre rolling resistance, we have

E_{\text{total car over distance d}}=E_{\text{air resistance}}+E_{\text{rolling resistance}}

E_{drag}\cong 0.65\cdot v_{car}^{2}\cdot d+constant\cdot d

From the graphs it is seen that per unit distance the drag resistance dominates over the rolling resistance at higher car speeds.

E_{\text{tot}}\cong 0{.}7\cdot v^{2}\cdot d

The energy consumption over a distance and the air pollution are proportional to the speed squared

The energy consumption of a car at higher speeds is seen to be proportional to its speed $v$ squared, and of course also to the distance $d$ traveled. So if the air resistance on the car dominates – and acceleration/braking and rolling resistance are of less significance for energy consumption, such as on the highway – the energy consumption is proportional to the square of the car speed. If air pollution increases in line with petrol consumption, this means that traveling at 120 km/h over the same distance pollutes 15% less than at 130 km/hour, because (120/130)² = 0.85 = 85% and 100% - 85% = 15%.

Because a car mainly produces heat and only uses 25% of the energy from the fuel for movement (an electric car uses about 90% for movement),[11] the petrol must provide much more energy than the car uses for movement:

E_{\text{supplied by gasoline}}=4\times E_{tot}\cong 2{,}8\cdot v^{2}\cdot d

Car power is proportional to the cube of the speed

Car power scales with the third power of the top speed for different car brands (Ferrari, Porsche, Opel Kadett, and Panda). Logarithmic scales. Tennekes, H.: Simple Science of Flight, MIT Press 2009. Used by David J.C. MacKay: Sustainable Energy - without the hot air, 2009.

Precise details of a car's energy consumption depend on the construction etc. of a car, but in general this quadratic relationship with speed is correct for speeds above 60 km/h, but refer to the accompanying figure.[1] This can also be seen in the measured relationship between the power (energy per time, so energy times speed divided by distance) $P_{car}$ of cars and the cube of their top speeds $v_{\text{top}}$ [16]

P_{top,car}=E_{top,car}/t=E_{top,car}/(d/v_{\text{top}})=E_{top,car}\cdot v_{\text{top}}/d\cong v_{\text{top}}^{3}

, so

P_{top,car}\cong v_{\text{top}}^{3}

Energy is proportional to the square of the speed and must be multiplied again by the speed to obtain the expended power. So the car power scales with the third power of the car speed. The consumption of energy per second increases eightfold (2³) if you drive twice faster.

General physics reference

Fundamentals of Physics: Halliday, David; Resnick, Robert; Walker, Jearl (1993). Fundamentals of physics. Fourth edition. Extended, with modern physics (4th ed.). New York, Chichester, Brisbane, Toronto, Singapore: John Wiley & Sons. ISBN 0471600121. OCLC 31514817.

References

MacKay, David J.C. (2009). Sustainable Energy – without the hot air. Cambridge: UIT. pp. 254–261. ISBN 9780954452933. OCLC 986577242. Retrieved 22 October 2023.. PDF free download. David J.C. MacKay (2009): Sustainable energy without the hot air, UIT Cambridge.
Benson, Harris (1996). University Physics Revised edition. New York: John Wiley & Sons. pp. 144–145. ISBN 9780471006893. OCLC 1403779613.
Hans van Baalen et al. (2006): Systematische natuurkunde, VWO 4 Kernboek A, Baarn Nijgh Versluys, p. 284, 301-302. In Dutch
Pieter Hogenbirk et al. (2009): Natuurkunde overal. Na Vwo deel 2, Noordhoff, p. 29. In Dutch.
MacKay 2009, p. 254
Benson 1996.
Halliday et al. 1993, p. 171.
Halliday et al. 1993, p. 175.
MacKay 2009, pp. 125, 256.
Halliday et al. 1993, p. 138 and Essay E4-2.
MacKay 2009, p. 256
MacKay 2009, p. 255
MacKay 2009, p. 260
MacKay 2009, p. 258, for car rubber tyres on smooth roads
Halliday et al. 1993, p. 160.
Tennekes, H, Simple science of flight, MIT Press 2009, quoted by David J.C. MacKay: Sustainable energy without the hot air, Cambridge: UIT 2009, Appendix A - Cars II p. 260.

External links

MacKay, David (29 August 2015). "Sustainable Energy – without the hot air". withouthotair.com. Retrieved 22 October 2023. Previous book publication 2009. PDF free download.
Physics Classroom (2023). "Kinetic Energy". The Physics Classroom. Retrieved 2023-10-22.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[MacKay-1] MacKay, David J.C. (2009). Sustainable Energy – without the hot air. Cambridge: UIT. pp. 254–261. ISBN 9780954452933. OCLC 986577242. Retrieved 22 October 2023.. PDF free download. David J.C. MacKay (2009): Sustainable energy without the hot air, UIT Cambridge.

[2] Benson, Harris (1996). University Physics Revised edition. New York: John Wiley & Sons. pp. 144–145. ISBN 9780471006893. OCLC 1403779613.

[3] Hans van Baalen et al. (2006): Systematische natuurkunde, VWO 4 Kernboek A, Baarn Nijgh Versluys, p. 284, 301-302. In Dutch

[4] Pieter Hogenbirk et al. (2009): Natuurkunde overal. Na Vwo deel 2, Noordhoff, p. 29. In Dutch.

[5] MacKay 2009, p. 254

[6] Benson 1996.

[7] Halliday et al. 1993, p. 171.

[8] Halliday et al. 1993, p. 175.

[9] MacKay 2009, pp. 125, 256.

[10] Halliday et al. 1993, p. 138 and Essay E4-2.

[p256-11] MacKay 2009, p. 256

[p255-12] MacKay 2009, p. 255

[13] MacKay 2009, p. 260

[14] MacKay 2009, p. 258, for car rubber tyres on smooth roads

[15] Halliday et al. 1993, p. 160.

[16] Tennekes, H, Simple science of flight, MIT Press 2009, quoted by David J.C. MacKay: Sustainable energy without the hot air, Cambridge: UIT 2009, Appendix A - Cars II p. 260.