Electroreflectance

When an electric field is applied to a metal or semiconductor, the electronic structure of the material changes. The electrons (and other charged particles) will react to the electric field, by repositioning themselves within the material. Electrons in metals can relatively easily move around and are available in abundance. They will move in such a manner that they try to cancel the external electric field.[5] Since no metal is a perfect conductor, no metal will perfectly cancel the external electric field within the material. In semiconductors the electrons that are available will not be able to move around as easily as electrons in metals. This leads to a weaker response and weaker cancellation of the electric field. This has the effect that the electric field can penetrate deeper into a semiconductor than into a metal.

The optical reflectivity of a (semi-)conductor is based on the band structure of the material close to or at the surface of the material. For reflectivity to occur a photon has to have enough energy to overcome the bandgap of electrons at the Fermi surface. When the photon energy is smaller than the bandgap, the solid will be unable to absorb the energy of the photon by excitation of an electron to a higher energy. This means that the photon will not be re-emitted by the solid and thus not reflected. If the photon energy is large enough to excite an electron from the Fermi surface, the solid will re-emit the photon by decaying the electron back to the original energy. This is not exactly the same photon as the incident photon, as it has for example the opposite direction of the incident photon.[6]

By applying an electric field to the material, the band structure of the solid changes. This change in band structure leads to a different bandgap, which in turn leads to a difference in optical reflectivity.[7] The electric field, generally made by creating a potential difference,[8] leads to an altered Hamiltonian. Using analytical methods available, such as the Tight Binding method, it can be calculated that this altered Hamiltonian leads to a different band structure.

The combination of electron repositioning and the change in band structure due to an external electric field is called the field effect. Since the electric field has more influence on semiconductors than on metals, semiconductors are easier to use to observe the electroreflectance effect.

The optical reflection in (semi-)conductors happens mostly in the surface region of the material. Therefore, the band structure of this region is extra important. Band structure usually covers bulk material. For deviations from this structure, it is conventional to use a band diagram. In a band diagram the x-axis is changed from wavevector k in band structure diagrams to position x in the preferred direction. Usually, this positional direction is normal to the surface plane.

For semiconductors specifically, the band diagram near the surface of the material is important. When an electric field is present close to, or in the material, this will lead to a potential difference within the semiconductor. Dependent on the electric field, the semiconductor will become n- or p-like in the surface region.[6] From now on we will use that the semiconductor has become n-like at the surface. The bands near the surface will bend under the electrostatic potential of the applied electric field. This bending can be interpreted in the same way as the bending of the valence and conduction bands in a p-n-junction, when equilibrium has been reached. The result of this bending leads to a conduction band that comes close to the Fermi level. Therefore, the conduction band will begin to fill with electrons.[6] This change in band structure leads to a change in optical reflection of the semiconductor.[9]

Optical reflectivity and the Brillouin zones are closely linked, since the band gap energy in the Brillouin zone determines if a photon is absorbed or reflected. If the band gap energy in the Brillouin zone is smaller than the photon energy, the photon will be absorbed, while the photon will be transmitted/reflected if the band gap energy is larger than the photon energy. For example, the photon energies of visible light lie in a range between 1.8 eV (red light) and 3.1 eV (violet light), So if the band gap energy is larger than 3.2 eV, photons of visible light will not be absorbed, but reflected/transmitted: the material appears transparent. This is the case for diamond, quartz etc. But if the band gap is roughly 2.6 eV (this is the case for cadmium sulfide) only blue and violet light is absorbed, while red and green light are transmitted, resulting in a reddish looking material.[6]

When an electric field is added to a (semi)conductor, the material will try to cancel this field by inducing an electric field at its surface. Because of this electric field, the optical properties of the surface layer will change, due to the change in size of critical band gaps, and hence changing its energy. Since the change in band gap only occurs on the surface of the (semi)conductor, optical properties will not change in the core of bulk materials, but for very thin films, where almost all particles can be found at the surface, the optical properties can change: absorption or transmittance of certain wavelengths depending on the strength of the electric field. This can result in more accurate measurements in case there are multiple compounds in the semiconductor, practically canceling the background noise of data.

Commonly, the band gaps are smallest close to, or at the Brillouin zone boundary. Adding an electric field will alter the whole band structure of the material where the electric field penetrates, but the effect will be especially noticeable at the Brillouin zone boundary. When the smallest band gap changes in size, this alters the optical reflectivity of the material more than the change in an already larger band gap. This can be explained by noticing that the smallest band gap determines a lot of the reflectivity, as lower energy photons cannot be absorbed and re-emitted.

The optical properties of semiconductors are directly related to the dielectric constant of the material. This dielectric constant gives the ratio between the electric permeability of a material in relation to the permeability of a vacuum. The imaginary refractive index of a material is given by the square root of the dielectric constant. The reflectance ${\textstyle R}$ of a material can be calculated using the Fresnel equations.[10] A present electric field alters the dielectric constant and therefore alters the optical properties of the material, like the reflectance.

A solid in contact with a liquid, in the presence of an electric field, forms an electric double layer. This layer is present at the interface of the solid and liquid and it shields the charged surface of the solid. This electric double layer has an effect on the optical reflectivity of the solid as it changes the elastic light scattering properties. The formation of the electric double layer involves different timescales, such as the relaxation time and the charging time.

The relaxation time we can write as ${\textstyle \tau _{d}=\lambda _{D}^{2}/D}$ with ${\textstyle D}$ being the Diffusion constant and ${\textstyle \lambda _{D}}$ the Debye length.

The charging time can be expressed by ${\textstyle \tau _{c}=\lambda _{D}L/D}$ where ${\textstyle L}$ is the representative system size.

The Debye length is often used as a measure of electric double layer thickness. Measuring the electric double layer with electroreflectance is challenging due to separation caused by conduction electrons.[11]

Using electroreflectance in surface physics studies gives some major advantages over techniques used before its discovery. Before, the determination of the surface potential was the hard to do since you need electrical measurements at the surface and it was difficult to probe the surface region without involving the bulk underneath. Electroreflectance does not need to make electrical measurements on the surface, but only uses optical measurements. Furthermore, due to direct functional relationships between surface potential and reflectivity we can get rid of a lot assumptions about mobility, scattering, or trapping of added carriers needed in the older methods. The electric field of the surface is probed by the modulation of the beam reflected by the surface. The incoming beam does not penetrate the material deep, so you only probe the surface without interacting with the bulk underneath.[13]

A simple gaussian wave with its 1st and 2nd derivative. As you take a higher order derivative the peak gets more pronounced since the peak gets narrower.

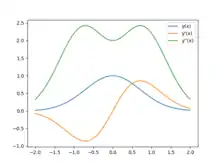
Third order spectroscopy, sometimes revered to as Aspnes's third-derivative, is a technique used to enhance the resolution of a spectroscopy measurement. This technique was first used by D.E. Aspnes to study electroreflectance in 1971.[14] Using 3rd order derivatives can sharpen the peak of a function (see figure). Especially in spectroscopy, where the wave is never measured on one specific wavelength, but always on a band, it is use full to sharpen the peak, and thus narrow the band.

Another advantage of derivatives is that baseline shifts are eliminated since derivatives get rid of shifts. These shifts in spectra can for example be caused by sample handling, lamp or detector instabilities. This way, you can eliminate some of the background noise of measurements.[15]

Wide band gap semiconductors like tin oxide ${\displaystyle {\ce {SnO2}}}$ generally possess a high chemical stability and mobility, are cheap to fabricate and have a suitable band alignment, making these semiconductors often used in various electronics as thin film transistors, anodes in lithium ion batteries and as electron transport layer in solar cells. The large band gap of ${\displaystyle {\ce {SnO2}}}$ (${\displaystyle E_{gap}\sim 3.62eV}$) and large binding energy (${\displaystyle E_{bind}\sim 130meV}$) make it useful in ultraviolet based devices.

But a fundamental problem arises with its dipole forbidden band structure in bulk form: the transition from the valence to the conduction band is dipole forbidden since both types of states exist with even parity with the effect that band edge emission of ${\displaystyle {\ce {SnO2}}}$ is forbidden in nature. This can be offset by employing its reduced dimensional structure, partially destroying the crystal symmetry, turning the forbidden dipole transition into allowed ones. Observing optical transitions in ${\displaystyle {\ce {SnO2}}}$ at room temperature, however, is challenging due to the light absorbing efficiency in the UV region of the reduced ${\displaystyle {\ce {SnO2}}}$ structures being very weak and background scattering of electrons with lower energies. Using electroreflectance the optical transitions of thin films can be recovered: by placing a thin film in an electric field, the critical points of the optical transition will be enhanced while, due to a change in reflectivity, low energy background scattering is reduced.[16]

Organic compounds containing conjugate (i.e., alternate single-double) bonds can have semiconducting properties. The conductivity and mobility of those organic compounds however, are very low compared to inorganic semiconductors. Assuming the molecules of the organic semiconductor are lattices, the same procedure of electroreflectance of inorganic semiconductors can be applied for the organic ones. It should be noted though that there is a certain dualism in semiconductors: intra-molecular conduction (inside a molecule) and inter-molecular conduction (between molecules), which one should take into account doing measurements. Especially for thin films the band gaps of organic semiconductors can be accurately determined using this method.[17]