Dwell mechanism
A dwell mechanism (either a linkage or cam-follower type) is an intermittent motion mechanism that alternates forward and return motion with holding position(s).[1]
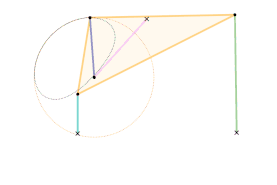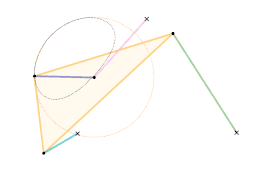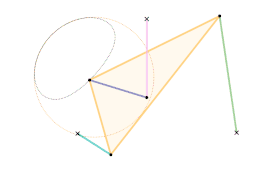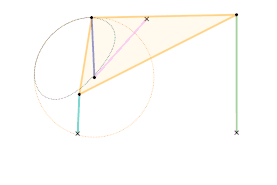
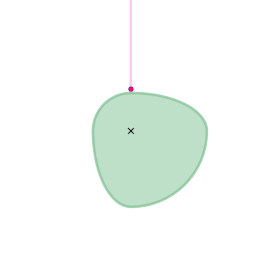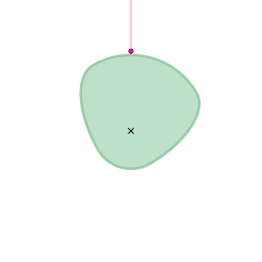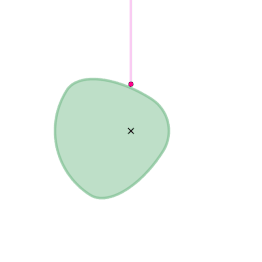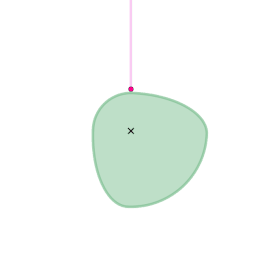
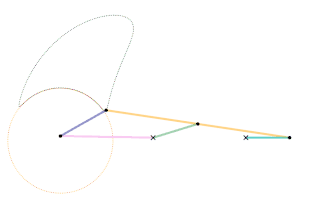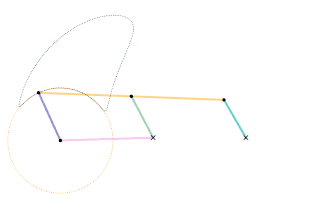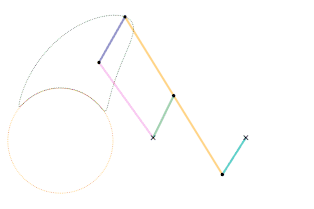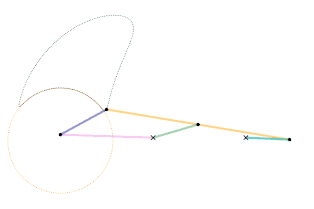
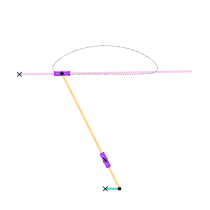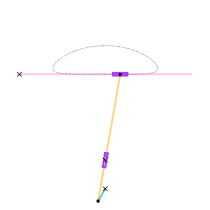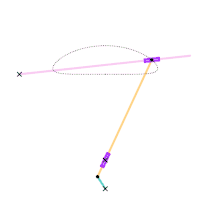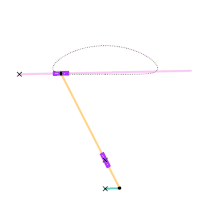
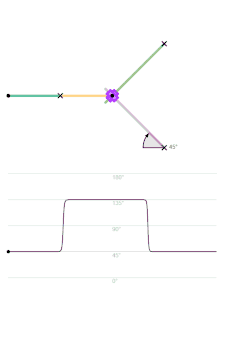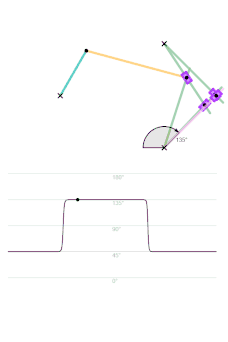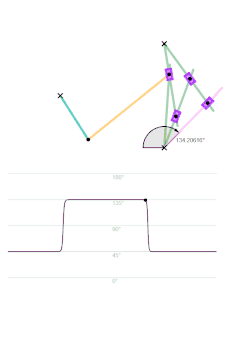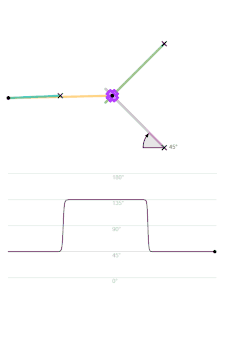
The orange circle shows the circular arc the coupler curve is approximating.
Dwells in cam mechanisms
Single dwell cam mechanisms
A single dwell cam mechanism has a motion function which follows a dwell-rise-fall sequence that repeats.
It is sometimes desired to use a rise function such that the acceleration of the follower is non-zero at its end of the rise. To maintain continuity, the fall function often begins such that the follower has the same non-zero acceleration as it had at the end of the rise function. The follower then stays stationary during the dwell function, with its velocity, acceleration, and jerk zero.[2]
There are a number of functions that can provide these motion requirements. A double-harmonic function is a common example used for single dwell.[3]
Double dwell cam mechanisms
A double dwell cam mechanism has a motion function which follows a rise-dwell-fall-dwell motion function sequence that repeats.
Unlike the single dwell, the rise function position ends with the follower's acceleration becoming zero, as it is stationary in the first dwell. Only after the first dwell does the acceleration become non-zero again during the fall function, returning the follower back to its original position and staying stationary again during the second dwell.
Dwells in linkage mechanisms
Dwell linkages cannot achieve a perfect dwell, unlike cam mechanisms, but rather have approximate dwells, where the output is remains roughly still.
Single dwell linkages
The orange circle shows the circular arc the coupler curve is approximating.
A single dwell linkage takes advantage of the behavior of a link with a stationary revolute (hinge) or prismatic (sliding) joint and its interaction with special coupler curves.
There are two methods of producing a single-dwell: arc-based and linear-based.
An arc-based single dwell linkage uses the approximation of a circular arc. The concept for linkage dwell mechanisms is that a node located at the center of the circular arc segment of a coupler curve will remain relatively stationary.
This is achieved first by choosing a desired coupler curve created by a four-bar linkage. Once a coupler curve is chosen, a circle is fit as closely as possible to a section of the coupler curve. The center of the fitted circle then becomes the position of the dyad: two links which are connected to the joint producing the coupler curve on one end by a revolute joint, and a stationary revolute joint on the other, creating the single dwell.[4]
A linear-based dwell uses a similar approach, but using an approximated straight line and a prismatic joint, in replacement of the revolute joint, for the dyad's connection to the coupler curve.
Double Dwell Linkages
The graph shows the relationship between the angle of the output link and time, with the input link rotating regularly.
There are several approaches to producing a double dwell linkage.
One such approach is to use a coupler curve with multiple approximated straight lines. Then, a dyad is positioned such that it is roughly tangential to both approximate straight lines. If the approximate straight lines are parallel, a pin and slider similar to that used in a scotch yoke mechanism can be used.
An extension to this approach is to use a quarter-circle arc produced by an oscillating link. A dyad with a prismatic joint can then be positioned such that the output link oscillates 90 degrees opposite of the oscillating link. This allows the design to be tile-able, with dyads to be appended onto each-other, and allow for double-dwells of any desirable occupied duration of the input stroke.
Although using the arc-based approach–the other method used for single-dwell linkages–is theoretically possible, it is significantly more difficult to execute and is impractical in practice, as both approximated arcs must share a circle of the same radius.
Compliant mechanisms and optimizations
Mechanisms have also been developed based on buckling beams and arcs.[5]
The actual dwell time will depend on the length of the approximate circular arc or straight line in the coupler curve. Initial designs may need optimization to improve the dwell characteristics.[6]
Applications
Cam-follower dwell mechanisms are used in pairs in sewing machines to operate the four motion feed dogs, with one cam moving the dog up and down, and the other cam moving the dog forwards and backwards. The cams in this application are usually phased 90 degrees apart allowing a pause in the up/down movement of the dog while it is being moved forwards/backwards. A separate adjustable sliding block or link is used to control the amount of forwards/backwards movement of the dog.
Industrial applications include loading and unloading parts, or transporting a part to a machine and holding it in place for a manufacturing process.[7]
Other applications include assembly lines, packaging machinery, machine tools, etc.
Further reading
- Norton, R (2009) Cam Design and Manufacturing Handbook, Industrial Press
- Rothbart, H (2003) Cam Design Handbook, McGraw Hill
References
- Uicker, J. Pennock, G. & Shigley, J. (2010). Theory of Machines and Mechanisms (4th ed.). Oxford University Press, p. 201.
- Doane, J. (2015) Machine Analysis with Computer Applications for Mechanical Engineers (1st ed.), Wiley, p299
- Norton, R. (2008) Design of Machinery (4th ed.), McGraw Hill, p.427
- Norton, R. (2008) Design of Machinery (4th ed.), McGraw Hill, p.147
- Sonmez, U (August 2007), "Introduction to Compliant Long Dwell Mechanism Designs Using Buckling Beams and Arcs", Journal of Mechanical Design, 129 (8): 831–843, CiteSeerX 10.1.1.1063.1373, doi:10.1115/1.2735337
- Doane, J. (2015) Machine Analysis with Computer Applications for Mechanical Engineers (1st ed.), Wiley, p167
- Doane, J. (2015) Machine Analysis with Computer Applications for Mechanical Engineers (1st ed.), Wiley, p167