Dowker–Thistlethwaite notation

In the mathematical field of knot theory, the Dowker–Thistlethwaite (DT) notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.[1]

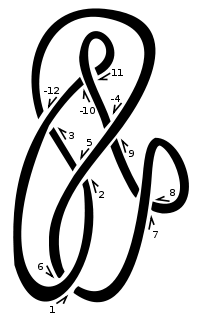
A knot diagram with crossings labelled for a Dowker sequence

Definition

To generate the Dowker–Thistlethwaite notation, traverse the knot using an arbitrary starting point and direction. Label each of the n crossings with the numbers 1, ..., 2n in order of traversal (each crossing is visited and labelled twice), with the following modification: if the label is an even number and the strand followed crosses over at the crossing, then change the sign on the label to be a negative. When finished, each crossing will be labelled a pair of integers, one even and one odd.[2] The Dowker–Thistlethwaite notation is the sequence of even integer labels associated with the labels 1, 3, ..., 2n − 1 in turn.

Example

For example, a knot diagram may have crossings labelled with the pairs (1, 6) (3, −12) (5, 2) (7, 8) (9, −4) and (11, −10). The Dowker–Thistlethwaite notation for this labelling is the sequence: 6 −12 2 8 −4 −10.

Uniqueness and counting

Dowker and Thistlethwaite have proved that the notation specifies prime knots uniquely, up to reflection.[1]

In the more general case, a knot can be recovered from a Dowker–Thistlethwaite sequence, but the recovered knot may differ from the original by either being a reflection or by having any connected sum component reflected in the line between its entry/exit points – the Dowker–Thistlethwaite notation is unchanged by these reflections. Knots tabulations typically consider only prime knots and disregard chirality, so this ambiguity does not affect the tabulation.

The ménage problem, posed by Tait, concerns counting the number of different number sequences possible in this notation.

See also

References
  1. Dowker, C. H.; Thistlethwaite, Morwen B. (1983-07-01). "Classification of knot projections". Topology and Its Applications. 16 (1): 19–31. doi:10.1016/0166-8641(83)90004-4. ISSN 0166-8641.
  2. Gukov, Sergei; Halverson, James; Ruehle, Fabian; Sułkowsk, Piotr (2021). "Learning to unknot". Machine Learning: Science and Technology. IOPscience. doi:10.1088/2632-2153/abe91f.

Further reading
  • Adams, Colin Conrad (2001). The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. Providence, R.I.: American Mathematical Soc. ISBN 978-0-8218-3678-1.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.