Dot planimeter

A dot planimeter is a device used in planimetrics for estimating the area of a shape, consisting of a transparent sheet containing a square grid of dots. To estimate the area of a shape, the sheet is overlaid on the shape and the dots within the shape are counted. The estimate of area is the number of dots counted multiplied by the area of a single grid square. In some variations, dots that land on or near the boundary of the shape are counted as half of a unit. The dots may also be grouped into larger square groups by lines drawn onto the transparency, allowing groups that are entirely within the shape to be added to the count rather than requiring their dots to be counted one by one.[1]

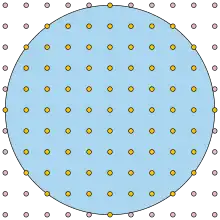
A radius-5 circle overlaid with a grid of dots in the pattern of a dot planimeter. When counting dots near the boundary of the shape as 1/2, there are 69 interior dots and 20 boundary dots for an estimated area of 79, close to the actual area of 25π ≈ 78.54.

The estimation of area by means of a dot grid has also been called the dot grid method or (particularly when the alignment of the grid with the shape is random) systematic sampling.[2] Perhaps because of its simplicity, it has been repeatedly reinvented.[3][4][5]

Application

In forestry, cartography, and geography, the dot planimeter has been applied to maps to estimate the area of parcels of land.[1][4][5][6] In botany and horticulture, it has been applied directly to sampled leaves to estimate the average leaf area.[7][8][9]

In medicine, it has been applied to Lashley diagrams as an estimate of the size of brain lesions.[10]

In mineralogy, a similar technique of counting dots in a grid is applied to cross-sections of rock samples for a different purpose, estimating the relative proportions of different constituent minerals.[11]

Theory

Greater accuracy can be achieved by using a dot planimeter with a finer grid of dots.[6] Alternatively, repeatedly placing a dot planimeter with different irrational offsets from its previous placement, and averaging the resulting measurements, can lead to a set of sampled measurements whose average tends towards the true area of the measured shape.[3] The method using a finer grid tends to have better statistical efficiency than repeated measurement with random placements.[2]

According to Pick's theorem, published by Georg Alexander Pick in 1899, the version of the dot planimeter with boundary dots counting as 1/2 (and with an added correction term of −1) gives exact results for polygons that have the dots as their vertices.[12][13] According to Blichfeldt's theorem, published by Hans Frederick Blichfeldt in 1914, it is always possible to shift a dot planimeter relative to a given shape without rotating it so that the number of dots within the shape is at least equal to its area.[14][15]

The Gauss circle problem concerns the error that would be obtained by using a dot planimeter to estimate the area of a circle. As its name suggests, it was studied in the early 19th century by Carl Friedrich Gauss. The maximum error is known to be bounded by a fractional power of the radius of the circle, with exponent between 1/2 and 131/208.[16]

The dot planimeter differs from other types of planimeter, which measure the area of a shape by passing a device around its boundary.[5]

The Steinhaus longimeter is a similar transparency-based device for estimating the length of curves by counting crossings.[17]

References
  1. Crommer, D. A. N. (January 1949), "Extracting small irregular areas", Australian Forestry, 13 (1): 64–66, doi:10.1080/00049158.1949.10675768
  2. Bellhouse, D. R. (1981), "Area estimation by point-counting techniques", Biometrics, 37 (2): 303–312, doi:10.2307/2530419, JSTOR 2530419, MR 0673040
  3. Steinhaus, Hugo (1924), "O mierzeniu pól płaskich" (PDF), Przegląd Matematyczno-Fizyczny (in Polish), 2 (1–2): 24–29
  4. Abell, C. A. (1939), "A method of estimating area in irregularly shaped and broken figures" (PDF), Journal of Forestry, 37: 344–345
  5. Wood, Walter F. (January 1954), "The dot planimeter, a new way to measure map area", The Professional Geographer, 6 (1): 12–14, doi:10.1111/j.0033-0124.1954.61_12.x
  6. Frolov, Y. S.; Maling, D. H. (June 1969), "The accuracy of area measurement by point counting techniques", The Cartographic Journal, 6 (1): 21–35, doi:10.1179/caj.1969.6.1.21
  7. Heinicke, Don R. (October 1963), "Note on estimation of leaf area and leaf distribution in fruit trees", Canadian Journal of Plant Science, Canadian Science Publishing, 43 (4): 597–598, doi:10.4141/cjps63-117
  8. Benjamin, D. M.; Freeman, G. H.; Brown, E. S. (February 1968), "The determination of irregularly-shaped areas of leaves destroyed by chewing insects", Annals of Applied Biology, 61 (1): 13–17, doi:10.1111/j.1744-7348.1968.tb04505.x
  9. Dolph, Gary E. (July–September 1977), "The effect of different calculational techniques on the estimation of leaf area and the construction of leaf size distributions", Bulletin of the Torrey Botanical Club, 104 (3): 264–269, doi:10.2307/2484308, JSTOR 2484308
  10. Thomas, Roger K.; Peacock, L. J. (January 1965), "A method of measuring brain lesions", Psychonomic Science, 3 (1–12): 184, doi:10.3758/bf03343085
  11. Neilson, M. J.; Brockman, G. F. (December 1977), "The error associated with point-counting", American Mineralogist, 62 (11–12): 1238–1244
  12. Pick, Georg (1899), "Geometrisches zur Zahlenlehre", Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" in Prag, (Neue Folge) (in German), 19: 311–319, JFM 33.0216.01 CiteBank:47270
  13. Wells, David (1991), "Pick's theorem", The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, pp. 183–184
  14. Blichfeldt, H. F. (1914), "A new principle in the geometry of numbers, with some applications", Transactions of the American Mathematical Society, 15 (3): 227–235, doi:10.1090/S0002-9947-1914-1500976-6, JSTOR 1988585, MR 1500976
  15. Olds, C. D.; Lax, Anneli; Davidoff, Giuliana P. (2000), "Chapter 9: A new principle in the geometry of numbers", The Geometry of Numbers, Anneli Lax New Mathematical Library, vol. 41, Mathematical Association of America, Washington, DC, pp. 119–127, ISBN 0-88385-643-3, MR 1817689
  16. Guy, Richard K. (2004), "F1: Gauß's lattice point problem", Unsolved Problems in Number Theory, Problem Books in Mathematics, vol. 1 (3rd ed.), New York: Springer-Verlag, pp. 365–367, doi:10.1007/978-0-387-26677-0, ISBN 0-387-20860-7, MR 2076335
  17. Steinhaus, Hugo (1931), "Longimetr", Czasopismo Geograficzne (in Polish), 3: 1–4
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.