Dipole graph
In graph theory, a dipole graph, dipole, bond graph, or linkage, is a multigraph consisting of two vertices connected with a number of parallel edges. A dipole graph containing n edges is called the order-n dipole graph, and is denoted by Dn. The order-n dipole graph is dual to the cycle graph Cn.
| Dipole graph | |
|---|---|
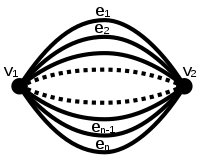 | |
| Vertices | 2 |
| Edges | n |
| Diameter | 1 (for n ≥ 1) |
| Chromatic number | 2 |
| Chromatic index | n |
| Properties | connected (for n ≥ 1) planar |
| Table of graphs and parameters | |
The honeycomb as an abstract graph is the maximal abelian covering graph of the dipole graph D3, while the diamond crystal as an abstract graph is the maximal abelian covering graph of D4.
Similarly to the Platonic graphs, the dipole graphs form the skeletons of the hosohedra. Their duals, the cycle graphs, form the skeletons of the dihedra.
References
- Weisstein, Eric W. "Dipole Graph". MathWorld.
- Jonathan L. Gross and Jay Yellen, 2006. Graph Theory and Its Applications, 2nd Ed., p. 17. Chapman & Hall/CRC. ISBN 1-58488-505-X
- Sunada T., Topological Crystallography, With a View Towards Discrete Geometric Analysis, Springer, 2013, ISBN 978-4-431-54176-9 (Print) 978-4-431-54177-6 (Online)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.