Cyclogon

In geometry, a cyclogon is the curve traced by a vertex of a regular polygon that rolls without slipping along a straight line.[1][2]

In the limit, as the number of sides increases to infinity, the cyclogon becomes a cycloid.[3]

The cyclogon has an interesting property regarding its area.[3] Let A denote the area of the region above the line and below one of the arches, let P denote the area of the rolling polygon, and let C denote the area of the disk that circumscribes the polygon. For every cyclogon generated by a regular polygon,

Examples

Cyclogons generated by an equilateral triangle and a square
Animation showing the generation of one arch of a cyclogon by an equilateral triangle as the triangle rolls over a straight line without slipping.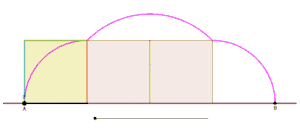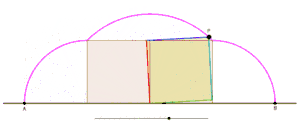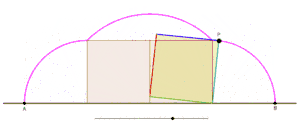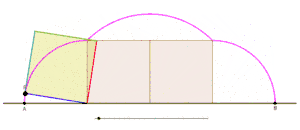
Animation showing the generation of one arch of a cyclogon by a square as the square rolls over a straight line without slipping.

 

Prolate cyclogon generated by an equilateral triangle
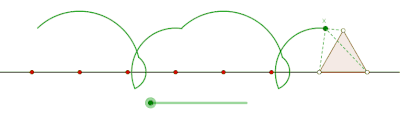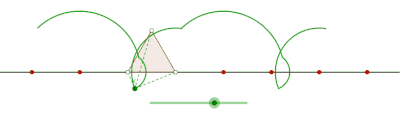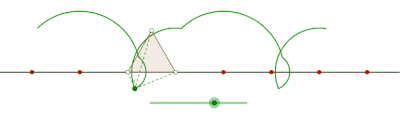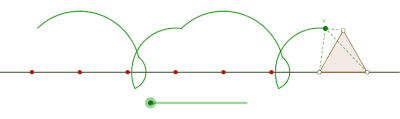
Animation showing the tracing of a prolate cyclogon as an equilateral triangle rolls over a straight line without skipping. The tracing point X is outside the disk of the triangle.

 

Curtate cyclogon generated by an equilateral triangle
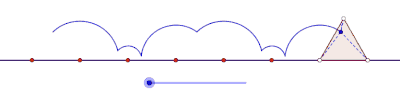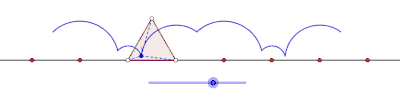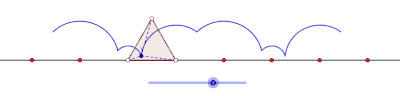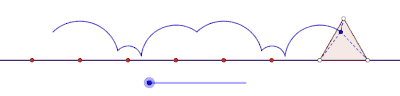
Animation showing the tracing of a curtate cyclogon as an equilateral triangle rolls over a straight line without skipping. The tracing point Y is inside the disk of the triangle.

Cyclogons generated by quadrilaterals
Cyclogon generated by a convex quadrilateral
Cyclogon generated by a non-convex quadrilateral
Cyclogon generated by a star-like quadrilateral

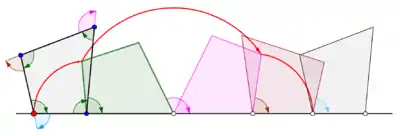
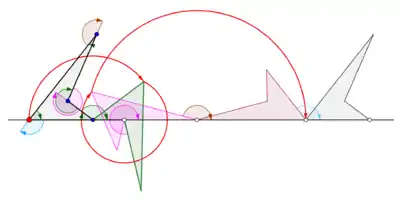
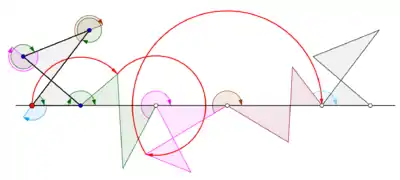
Generalized cyclogons

A cyclogon is obtained when a polygon rolls over a straight line. Let it be assumed that the regular polygon rolls over the edge of another polygon. Let it also be assumed that the tracing point is not a point on the boundary of the polygon but possibly a point within the polygon or outside the polygon but lying in the plane of the polygon. In this more general situation, let a curve be traced by a point z on a regular polygonal disk with n sides rolling around another regular polygonal disk with m sides. The edges of the two regular polygons are assumed to have the same length. A point z attached rigidly to the n-gon traces out an arch consisting of n circular arcs before repeating the pattern periodically. This curve is called a trochogon — an epitrochogon if the n-gon rolls outside the m-gon, and a hypotrochogon if it rolls inside the m-gon. The trochogon is curtate if z is inside the n-gon, and prolate (with loops) if z is outside the n-gon. If z is at a vertex it traces an epicyclogon or a hypocyclogon.[4]

See also

References
  1. Tom M. Apostol, Mamikon Mnatsakanian (2012). New Horizons in Geometry. Mathematical Association of America. p. 68. ISBN 9780883853542.
  2. Ken Caviness. "Cyclogons". Wolfram Demonstrations Project. Retrieved 23 December 2015.
  3. T. M. Apostol and M. A. Mnatsakanian (1999). "Cycloidal Areas without Calculus" (PDF). Math Horizons. 7 (1): 12–16. doi:10.1080/10724117.1999.12088451. Archived from the original (PDF) on 2005-01-30. Retrieved 23 December 2015.
  4. Tom M. Apostopl and Mamikon A. Mnatsaknian (September 2002). "Generalized Cyclogons" (PDF). Math Horizons. Archived from the original (PDF) on 2005-01-30. Retrieved 23 December 2015.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.