Conchoid of de Sluze

In algebraic geometry, the conchoids of de Sluze are a family of plane curves studied in 1662 by Walloon mathematician René François Walter, baron de Sluze.[1][2]

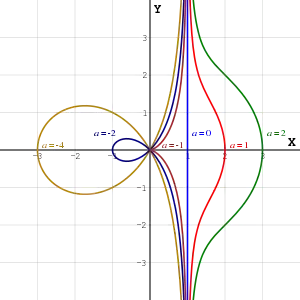
The Conchoid of de Sluze for several values of a

The curves are defined by the polar equation

${\displaystyle r=\sec \theta +a\cos \theta \,.}$

In cartesian coordinates, the curves satisfy the implicit equation

${\displaystyle (x-1)(x^{2}+y^{2})=ax^{2}\,}$

except that for a = 0 the implicit form has an acnode (0,0) not present in polar form.

They are rational, circular, cubic plane curves.

These expressions have an asymptote x = 1 (for a ≠ 0). The point most distant from the asymptote is (1 + a, 0). (0,0) is a crunode for a < −1.

The area between the curve and the asymptote is, for a ≥ −1,

${\displaystyle |a|(1+a/4)\pi \,}$

while for a < −1, the area is

${\displaystyle \left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}-a\left(2+{\frac {a}{2}}\right)\arcsin {\frac {1}{\sqrt {-a}}}.}$

If a < −1, the curve will have a loop. The area of the loop is

${\displaystyle \left(2+{\frac {a}{2}}\right)a\arccos {\frac {1}{\sqrt {-a}}}+\left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}.}$

Four of the family have names of their own:

• a = 0, line (asymptote to the rest of the family)
• a = −1, cissoid of Diocles
• a = −2, right strophoid
• a = −4, trisectrix of Maclaurin