Phylogenetic comparative methods

Phylogenetic comparative approaches can complement other ways of studying adaptation, such as studying natural populations, experimental studies, and mathematical models.[6] Interspecific comparisons allow researchers to assess the generality of evolutionary phenomena by considering independent evolutionary events. Such an approach is particularly useful when there is little or no variation within species. And because they can be used to explicitly model evolutionary processes occurring over very long time periods, they can provide insight into macroevolutionary questions, once the exclusive domain of paleontology.[4]

Home range areas of 49 species of mammals in relation to their body size. Larger-bodied species tend to have larger home ranges, but at any given body size members of the order Carnivora (carnivores and omnivores) tend to have larger home ranges than ungulates (all of which are herbivores). Whether this difference is considered statistically significant depends on what type of analysis is applied[7]

Testes mass of various species of Primates in relation to their body size and mating system. Larger-bodied species tend to have larger testes, but at any given body size species in which females tend to mate with multiple males have males with larger testes.

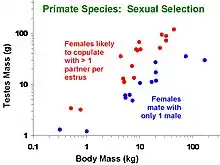
Phylogenetic comparative methods are commonly applied to such questions as:

• What is the slope of an allometric scaling relationship?

→ Example: how does brain mass vary in relation to body mass?

• Do different clades of organisms differ with respect to some phenotypic trait?

→ Example: do canids have larger hearts than felids?

• Do groups of species that share a behavioral or ecological feature (e.g., social system, diet) differ in average phenotype?

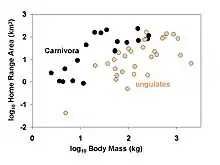
→ Example: do carnivores have larger home ranges than herbivores?

• What was the ancestral state of a trait?

→ Example: where did endothermy evolve in the lineage that led to mammals?

→ Example: where, when, and why did placentas and viviparity evolve?

• Does a trait exhibit significant phylogenetic signal in a particular group of organisms? Do certain types of traits tend to "follow phylogeny" more than others?

→ Example: are behavioral traits more labile during evolution?

• Do species differences in life history traits trade-off, as in the so-called fast-slow continuum?

→ Example: why do small-bodied species have shorter life spans than their larger relatives?

The standardized contrasts are used in conventional statistical procedures, with the constraint that all regressions, correlations, analysis of covariance, etc., must pass through the origin.

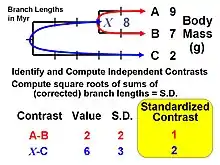
Felsenstein[1] proposed the first general statistical method in 1985 for incorporating phylogenetic information, i.e., the first that could use any arbitrary topology (branching order) and a specified set of branch lengths. The method is now recognized as an algorithm that implements a special case of what are termed phylogenetic generalized least-squares models.[8] The logic of the method is to use phylogenetic information (and an assumed Brownian motion like model of trait evolution) to transform the original tip data (mean values for a set of species) into values that are statistically independent and identically distributed.

The algorithm involves computing values at internal nodes as an intermediate step, but they are generally not used for inferences by themselves. An exception occurs for the basal (root) node, which can be interpreted as an estimate of the ancestral value for the entire tree (assuming that no directional evolutionary trends [e.g., Cope's rule] have occurred) or as a phylogenetically weighted estimate of the mean for the entire set of tip species (terminal taxa). The value at the root is equivalent to that obtained from the "squared-change parsimony" algorithm and is also the maximum likelihood estimate under Brownian motion. The independent contrasts algebra can also be used to compute a standard error or confidence interval.

Probably the most commonly used PCM is phylogenetic generalized least squares (PGLS).[8][9] This approach is used to test whether there is a relationship between two (or more) variables while accounting for the fact that lineage are not independent. The method is a special case of generalized least squares (GLS) and as such the PGLS estimator is also unbiased, consistent, efficient, and asymptotically normal.[10] In many statistical situations where GLS (or, ordinary least squares [OLS]) is used residual errors ε are assumed to be independent and identically distributed random variables that are assumed to be normal

${\displaystyle \varepsilon \mid X\sim {\mathcal {N}}(0,\sigma ^{2}I_{n}).}$

whereas in PGLS the errors are assumed to be distributed as

${\displaystyle \varepsilon \mid X\sim {\mathcal {N}}(0,\mathbf {V} ).}$

where V is a matrix of expected variance and covariance of the residuals given an evolutionary model and a phylogenetic tree. Therefore, it is the structure of residuals and not the variables themselves that show phylogenetic signal. This has long been a source of confusion in the scientific literature.[11] A number of models have been proposed for the structure of V such as Brownian motion[8] Ornstein-Uhlenbeck,[12] and Pagel's λ model.[13] (When a Brownian motion model is used, PGLS is identical to the independent contrasts estimator.[14]). In PGLS, the parameters of the evolutionary model are typically co-estimated with the regression parameters.

PGLS can only be applied to questions where the dependent variable is continuously distributed; however, the phylogenetic tree can also be incorporated into the residual distribution of generalized linear models, making it possible to generalize the approach to a broader set of distributions for the response.[15][16][17]

Data for a continuous-valued trait can be simulated in such a way that taxa at the tips of a hypothetical phylogenetic tree will exhibit phylogenetic signal, i.e., closely related species will tend to resemble each other.

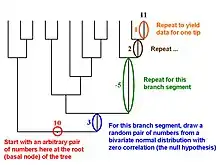
Martins and Garland[18] proposed in 1991 that one way to account for phylogenetic relations when conducting statistical analyses was to use computer simulations to create many data sets that are consistent with the null hypothesis under test (e.g., no correlation between two traits, no difference between two ecologically defined groups of species) but that mimic evolution along the relevant phylogenetic tree. If such data sets (typically 1,000 or more) are analyzed with the same statistical procedure that is used to analyze a real data set, then results for the simulated data sets can be used to create phylogenetically correct (or "PC"[7]) null distributions of the test statistic (e.g., a correlation coefficient, t, F). Such simulation approaches can also be combined with such methods as phylogenetically independent contrasts or PGLS (see above).

• Adaptation and the comparative method online lecture, with worked example of phylogenetically independent contrasts and mastery quiz
• List of phylogeny programs
• Phylocomm
• Phylogenetic Tools for Comparative Biology
• Phylogeny of Sleep website
• Tree of Life