Circle of equal altitude
The circle of equal altitude, also called circle of position (CoP), is defined as the locus of points on Earth on which an observer sees a celestial object such as the sun or a star, at a given time, with the same observed altitude. It was discovered by the American sea-captain Thomas Hubbard Sumner in 1837, published in 1843 and is the basis of an important method in celestial navigation.
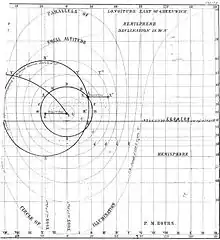
Discovery
Sumner discovered the line on a voyage from South Carolina to Greenock in Scotland in 1837. On December 17, as he was nearing the coast of Wales, he was uncertain of his position after several days of cloudy weather and no sights. A momentary opening in the clouds allowed him to determine the altitude of the sun. This, together with the chronometer time and the latitude enabled him to calculate the longitude. But he was not confident of his latitude, which depended on dead reckoning (DR). So he calculated longitude using his DR value and two more values of latitude 10' and 20' to the north. He found that the three positions were on a straight line which happened to pass through Smalls Lighthouse. He realised that he must be located somewhere on that line and that if he set course E.N.E. along the line he should eventually sight the Smalls Light which, in fact he did, in less than an hour. Having found the line empirically, he then worked out the theory, and published this in a book in 1843. The method was quickly recognized as an important development in celestial navigation, and was made available to every ship in the United States Navy.[1]
Parameters
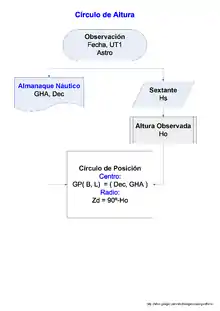
The center of the CoP, is the geographical position (GP) of the observed body, the substellar point for a star, the subsolar point for the sun. The radius is the great circle distance equal to the zenith distance of the body.
- Center = geographical position (GP) of the body: (, ) = (Dec, -GHA)
- If is defined as west longitude (+W/-E) then it will be +GHA, since HA (GHA or LHA) is always measured west-ward (+W/-E).
- Radius = zenith distance: zd [nm] = 60 ⋅ (90 - Ho) (aka co-altitude of Ho)
As the circles used for navigation generally have a radius of thousands of miles, a segment a few tens of miles long closely approximates a straight line, as described in Sumner's original use of the method.
Equation
The equation links the following variables[2]
- The position of the observer: B, L.
- The coordinates of the observed star, its geographical position: GHA, Dec.
- The true altitude of the body: Ho.
Being B the latitude (+N/-S), L the longitude (+E/-W). LHA = GHA + L is the local hour angle (+W/-E), Dec and GHA are the declination and Greenwich hour angle of the star observed. And Ho is the true or observed altitude, that is, the altitude measured with a sextant corrected for dip, refraction and parallax.
Special cases of COPs
- Parallel of latitude by Polaris altitude.
- Parallel of latitude by altitude of the sun at noon, or meridian altitude.
- Meridian of longitude known the time and latitude.
- Circle of illumination or terminator (star = Sun, Ho = 0 for places at Sunrise/Sunset).
See also
References
- Richardson, Robert S. (1943). "Captain Thomas Hubbard Sumner, 1807-1876". Publications of the Astronomical Society of the Pacific. 55 (324): 136–144. Bibcode:1943PASP...55..136R. doi:10.1086/125525. JSTOR 40669797. S2CID 110650268.
- Vector equation of the Circle of Position
External links
- Navigational Algorithms http://sites.google.com/site/navigationalalgorithms/ Papers: Vector equation of the Circle of Position, Use of rotation matrices to plot a circle of equal altitude. Software: Plotting of the circumferences of equal altitude
- Correction to the sextant altitude Archivo:CorrecionHs.jpg