Borsuk's conjecture
The Borsuk problem in geometry, for historical reasons[note 1] incorrectly called Borsuk's conjecture, is a question in discrete geometry. It is named after Karol Borsuk.
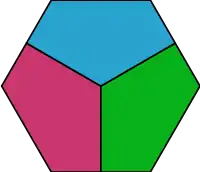
Problem
In 1932, Karol Borsuk showed[2] that an ordinary 3-dimensional ball in Euclidean space can be easily dissected into 4 solids, each of which has a smaller diameter than the ball, and generally n-dimensional ball can be covered with n + 1 compact sets of diameters smaller than the ball. At the same time he proved that n subsets are not enough in general. The proof is based on the Borsuk–Ulam theorem. That led Borsuk to a general question:[2]
Die folgende Frage bleibt offen: Lässt sich jede beschränkte Teilmenge E des Raumes in (n + 1) Mengen zerlegen, von denen jede einen kleineren Durchmesser als E hat?
The following question remains open: Can every bounded subset E of the space be partitioned into (n + 1) sets, each of which has a smaller diameter than E?
— Drei Sätze über die n-dimensionale euklidische Sphäre
The question was answered in the positive in the following cases:
- n = 2 — which is the original result by Karol Borsuk (1932).
- n = 3 — shown by Julian Perkal (1947),[3] and independently, 8 years later, by H. G. Eggleston (1955).[4] A simple proof was found later by Branko Grünbaum and Aladár Heppes.
- For all n for smooth convex bodies — shown by Hugo Hadwiger (1946).[5][6]
- For all n for centrally-symmetric bodies — shown by A.S. Riesling (1971).[7]
- For all n for bodies of revolution — shown by Boris Dekster (1995).[8]
The problem was finally solved in 1993 by Jeff Kahn and Gil Kalai, who showed that the general answer to Borsuk's question is no.[9] They claim that their construction shows that n + 1 pieces do not suffice for n = 1325 and for each n > 2014. However, as pointed out by Bernulf Weißbach,[10] the first part of this claim is in fact false. But after improving a suboptimal conclusion within the corresponding derivation, one can indeed verify one of the constructed point sets as a counterexample for n = 1325 (as well as all higher dimensions up to 1560).[11]
Their result was improved in 2003 by Hinrichs and Richter, who constructed finite sets for n ≥ 298, which cannot be partitioned into n + 11 parts of smaller diameter.[1]
In 2013, Andriy V. Bondarenko had shown that Borsuk's conjecture is false for all n ≥ 65.[12] Shortly after, Thomas Jenrich derived a 64-dimensional counterexample from Bondarenko's construction, giving the best bound up to now.[13][14]
Apart from finding the minimum number n of dimensions such that the number of pieces α(n) > n + 1, mathematicians are interested in finding the general behavior of the function α(n). Kahn and Kalai show that in general (that is, for n sufficiently large), one needs many pieces. They also quote the upper bound by Oded Schramm, who showed that for every ε, if n is sufficiently large, .[15] The correct order of magnitude of α(n) is still unknown.[16] However, it is conjectured that there is a constant c > 1 such that α(n) > cn for all n ≥ 1.
See also
- Hadwiger's conjecture on covering convex bodies with smaller copies of themselves
- Kahn–Kalai conjecture
Note
- As Hinrichs and Richter say in the introduction to their work,[1] the "Borsuk's conjecture [was] believed by many to be true for some decades" (hence commonly called a conjecture) so "it came as a surprise when Kahn and Kalai constructed finite sets showing the contrary". It's worth noting, however, that Karol Borsuk has formulated the problem just as a question, not suggesting the expected answer would be positive.
References
- Hinrichs, Aicke; Richter, Christian (28 August 2003). "New sets with large Borsuk numbers". Discrete Mathematics. Elsevier. 270 (1–3): 137–147. doi:10.1016/S0012-365X(02)00833-6.
- Borsuk, Karol (1933), "Drei Sätze über die n-dimensionale euklidische Sphäre" (PDF), Fundamenta Mathematicae (in German), 20: 177–190, doi:10.4064/fm-20-1-177-190
- Perkal, Julian (1947), "Sur la subdivision des ensembles en parties de diamètre inférieur", Colloquium Mathematicum (in French), 2: 45
- Eggleston, H. G. (1955), "Covering a three-dimensional set with sets of smaller diameter", Journal of the London Mathematical Society, 30: 11–24, doi:10.1112/jlms/s1-30.1.11, MR 0067473
- Hadwiger, Hugo (1945), "Überdeckung einer Menge durch Mengen kleineren Durchmessers", Commentarii Mathematici Helvetici (in German), 18 (1): 73–75, doi:10.1007/BF02568103, MR 0013901, S2CID 122199549
- Hadwiger, Hugo (1946), "Mitteilung betreffend meine Note: Überdeckung einer Menge durch Mengen kleineren Durchmessers", Commentarii Mathematici Helvetici (in German), 19 (1): 72–73, doi:10.1007/BF02565947, MR 0017515, S2CID 121053805
- Riesling, A. S. (1971), "Проблема Борсука в трехмерных пространствах постоянной кривизны" [Borsuk's problem in three-dimensional spaces of constant curvature] (PDF), Ukr. Geom. Sbornik (in Russian), Kharkov State University (now National University of Kharkiv), 11: 78–83
- Dekster, Boris (1995), "The Borsuk conjecture holds for bodies of revolution", Journal of Geometry, 52 (1–2): 64–73, doi:10.1007/BF01406827, MR 1317256, S2CID 121586146
- Kahn, Jeff; Kalai, Gil (1993), "A counterexample to Borsuk's conjecture", Bulletin of the American Mathematical Society, 29 (1): 60–62, arXiv:math/9307229, doi:10.1090/S0273-0979-1993-00398-7, MR 1193538, S2CID 119647518
- Weißbach, Bernulf (2000), "Sets with Large Borsuk Number" (PDF), Beiträge zur Algebra und Geometrie (in German), 41 (2): 417–423
- Jenrich, Thomas (2018), On the counterexamples to Borsuk's conjecture by Kahn and Kalai, arXiv:1809.09612v4
- Bondarenko, Andriy (2014) [2013], "On Borsuk's Conjecture for Two-Distance Sets", Discrete & Computational Geometry, 51 (3): 509–515, arXiv:1305.2584, doi:10.1007/s00454-014-9579-4, MR 3201240
- Jenrich, Thomas (2013), A 64-dimensional two-distance counterexample to Borsuk's conjecture, arXiv:1308.0206, Bibcode:2013arXiv1308.0206J
- Jenrich, Thomas; Brouwer, Andries E. (2014), "A 64-Dimensional Counterexample to Borsuk's Conjecture", Electronic Journal of Combinatorics, 21 (4): #P4.29, doi:10.37236/4069, MR 3292266
- Schramm, Oded (1988), "Illuminating sets of constant width", Mathematika, 35 (2): 180–189, doi:10.1112/S0025579300015175, MR 0986627
- Alon, Noga (2002), "Discrete mathematics: methods and challenges", Proceedings of the International Congress of Mathematicians, Beijing, 1: 119–135, arXiv:math/0212390, Bibcode:2002math.....12390A
Further reading
- Oleg Pikhurko, Algebraic Methods in Combinatorics, course notes.
- Andrei M. Raigorodskii, The Borsuk partition problem: the seventieth anniversary, Mathematical Intelligencer 26 (2004), no. 3, 4–12.
- Raigorodskii, Andreii M. (2008). "Three lectures on the Borsuk partition problem". In Young, Nicholas; Choi, Yemon (eds.). Surveys in contemporary mathematics. London Mathematical Society Lecture Note Series. Vol. 347. Cambridge University Press. pp. 202–247. ISBN 978-0-521-70564-6. Zbl 1144.52005.