Blaschke product
In complex analysis, the Blaschke product is a bounded analytic function in the open unit disc constructed to have zeros at a (finite or infinite) sequence of prescribed complex numbers
inside the unit disc, with the property that the magnitude of the function is constant along the boundary of the disc.
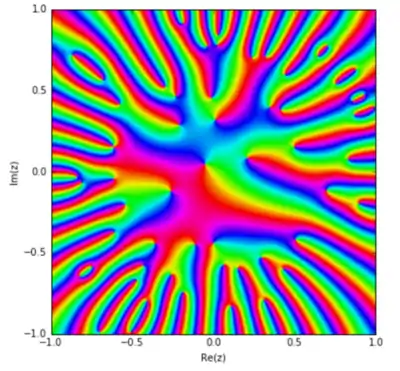
Blaschke products were introduced by Wilhelm Blaschke (1915). They are related to Hardy spaces.
Definition
A sequence of points inside the unit disk is said to satisfy the Blaschke condition when
Given a sequence obeying the Blaschke condition, the Blaschke product is defined as
with factors
provided . Here is the complex conjugate of . When take .
The Blaschke product defines a function analytic in the open unit disc, and zero exactly at the (with multiplicity counted): furthermore it is in the Hardy class .[1]
The sequence of satisfying the convergence criterion above is sometimes called a Blaschke sequence.
Szegő theorem
A theorem of Gábor Szegő states that if , the Hardy space with integrable norm, and if is not identically zero, then the zeroes of (certainly countable in number) satisfy the Blaschke condition.
Finite Blaschke products
Finite Blaschke products can be characterized (as analytic functions on the unit disc) in the following way: Assume that is an analytic function on the open unit disc such that can be extended to a continuous function on the closed unit disc
that maps the unit circle to itself. Then is equal to a finite Blaschke product
where lies on the unit circle and is the multiplicity of the zero , . In particular, if satisfies the condition above and has no zeros inside the unit circle, then is constant (this fact is also a consequence of the maximum principle for harmonic functions, applied to the harmonic function .
References
- Conway (1996) 274
- Blaschke, W. (1915). "Eine Erweiterung des Satzes von Vitali über Folgen analytischer Funktionen". Berichte Math.-Phys. Kl. (in German). Sächs. Gesell. der Wiss. Leipzig. 67: 194–200.
- Colwell, Peter (1985). Blaschke Products. Ann Arbor, Michigan: University of Michigan Press. ISBN 0-472-10065-3. MR 0779463.
- Conway, John B. Functions of a Complex Variable II. Graduate Texts in Mathematics. Vol. 159. Springer-Verlag. pp. 273–274. ISBN 0-387-94460-5.
- Tamrazov, P.M. (2001) [1994]. "Blaschke product". Encyclopedia of Mathematics. EMS Press.